18.2: Asignación de Mercado de Equilibrio General

El análisis de equilibrio parcial se basa en la oferta y la demanda de una mercancía en particular para explicar cómo el mercado establece un producto de equilibrio que es la respuesta de la sociedad a la pregunta de asignación de recursos. La cifra X trazada por líneas de oferta y demanda es quizás el cuadro más básico y conocido de la economía.

En comparación con la gráfica de oferta y demanda fácil y familiar, el análisis de equilibrio general trabaja y lucha con un nuevo gráfico, el Edgeworth Box, que resulta confuso cuando se encuentra por primera vez. Está ocupado, con muchos elementos, y requiere que el usuario cambie perseptivo para leerlo. Mientras trabaja en el dominio de Edgeworth Box, recuerde esto: el proceso de equilibrio en una Edgeworth Box se basa en la misma lógica utilizada en el análisis de oferta y demanda.

Aprovecharemos el conocimiento de la oferta y la demanda para explicar cómo funciona el equilibrio general y aprender a leer la Caja Edgeworth.

Tatonnement: El Proceso de Equilibración

Los estudiantes de economía introductoria saben que la escasez hace que los precios suban y los excedentes empujan los precios a la baja En una gráfica de oferta y demanda, el precio se muestra como una línea horizontal que cae cuando está por encima de la intersección y sube cuando está por debajo.

En el Edgeworth Box, hay dos mercados que equilibran simultáneamente. Los precios de los dos bienes se muestran por una sola línea, que es la restricción presupuestal que enfrentan los dos consumidores. La pendiente de la línea de precio, también conocida como el vector precio, es\(-\frac{p_1}{p_2}\).

Al igual que la oferta y la demanda, la escasez y los excedentes empujan los precios hacia arriba y hacia abajo. En la Caja Edgeworth, esto se traduce en el balanceo del vector de precios.

Recuerden que estamos considerando el caso especial de una economía puramente cambiaria. Todos los productos han sido producidos y los individuos están negociando desde sus dotaciones iniciales. Los precios están determinados de manera competitiva por la interacción de todos los compradores y vendedorescada consumidor toma los precios como se dan.

Una caja Edgeworth bidimensional permite solo dos consumidores. Un tercer consumidor lo convertiría en un cubo y, más allá de eso, nos quedamos sin dimensiones y no podemos dibujar el objeto (aunque exista). Nuestra versión de modelo de juguete para dos consumidores implementa un comportamiento de toma de precios al suponer que hay un subastador que grita precios. Nuestros consumidores toman estos precios como se dan y los utilizan para tomar decisiones de compra y venta.

Si bien cada mercancía tiene un precio, en el análisis de equilibrio general, solo importan los precios relativos. Podemos tomar arbitrariamente un bien y establecer su precio en 1. Esto hace que sea bueno el numerario.

Nuestros dos consumidores escuchan los precios y toman decisiones optimizadas basadas en esos precios. Si las decisiones de compra y venta no coinciden, los precios son ajustados por el subastador. En realidad, no se realizan operaciones hasta que todos los mercados estén en equilibrio.

A medida que los precios son señalados por el subastador, el vector de precios gira alrededor de la dotación inicial, oscilando de un lado a otro. Se vuelve más vertical a medida que\(\frac{p_1}{p_2}\) sube y más plano si\(\frac{p_1}{p_2}\) cae. Nos referimos, por supuesto, a subir y bajar en valor absoluto.

En cualquier momento, los consumidores pueden calcular las cantidades óptimas de cada bien para comprar y vender. Si las cantidades que cada uno quiere comprar y vender no son mutuamente compatibles, entonces el vector de precios se balancea hacia el vector de precio de equilibrio.

La palabra tâtonnement (pronunciado ta-tone-mon) fue utilizada por el economista francés Leon Walras (1834 - 1910) (pronunciado Val-rasse) para describir el proceso de equilibrado. Google lo traduce como manosear. Walras visualizó el mercado a tientas, sintiendo, abriéndose camino a través de un proceso iterativo que convergía a una posición de descanso. En la literatura técnica de la teoría del equilibrio general, la palabra tatonnement (sin el circunflejo) es aceptada sin cursiva.

Es posible que hayas notado que la terminología del análisis de equilibrio general tiene un sabor decididamente francófono a la misma. Walras, el padre de la teoría del equilibrio general (y descrito por Schumpeter como “el mayor economista de la historia”) era francés. Su sucesor en la Escuela de Lausana fue Vilfredo Pareto (1848 - 1923), un italiano nativo con formación en matemáticas e ingeniería, que inventó el concepto de optimalidad de Pareto (y es el verdadero creador de la Edgeworth Box).

En la segunda mitad del siglo XIX, los economistas de Europa continental estuvieron a la vanguardia de la teoría del equilibrio general y la economía matemática. Esta fuerte tradición matemática continúa hoy en día. Gerard Debreu y Maurice Allais, de origen francés, han ganado los Premios Nobel de Economía por su trabajo en teoría del equilibrio general.

Utilizaremos Excel para implementar un problema concreto con los precios reales, los excedentes y la escasez para ver cómo funciona el modelo walrasiano.

PASO Abra el libro de Excel EdgeworthBoxGE.xls, lea la hoja de introducción, luego vaya a la hoja EdgeWorthBox1.

Revisamos el expositor, pieza por pieza. Vale la pena ir despacio y tener cuidado. Están pasando muchas cosas y los detalles importan.

El problema de optimización del consumidor A está en las columnas A y B. No es necesario ejecutar Solvercells B11 y B12 que contienen la expresión óptima de forma reducida de A. Con un vector de precio con pendiente\(-\frac{2}{3}\), al consumidor A le gustaría vender 10 unidades de bien 1 y comprar\(6 \frac{2}{3}\) unidades de bien 2.

Las columnas M y N muestran el problema de optimización del consumidor B. Al igual que A, hemos ingresado las fórmulas de forma reducida para el consumo óptimo de B de los dos bienes. A los precios iniciales, el consumidor B quiere comprar 20 unidades de bien 1 y vender\(13 \frac{1}{3}\) unidades de bien 2.

Esta información es todo lo que necesitamos saber que el precio\(p_1\) relativo en la celda H16 no es un precio de equilibrio, ni de compensación de mercado. Después de todo, A quiere vender\(x_1\) más de lo que B quiere comprar y viceversa para\(x_2\).

Así, no se realizarán operaciones a estos precios y el subastador walrasiano llamará nuevos precios a medida que continúe la búsqueda del equilibrio.

También podemos usar el Edgeworth Box para llegar a esta misma conclusión sobre los planes que no coinciden al precio relativo inicial de\(-0.67\).

PASO Desplácese hacia abajo para ver la caja Edgeworth.

La Figura 18.4 reproduce una porción de lo que hay en tu pantalla, aumentada con flechas y líneas discontinuas para ayudar a explicar lo que está pasando.

Figura 18.4: Una caja de Edgeworth en desequilibrio.

Fuente: EdgeworthBoxGE.xls! EdgeWorthBox1.

Comenzamos por A, que es más fácil que B. En la Figura 18.4, las flechas a lo largo de los lados inferior e izquierdo de la caja indican lo que A quiere hacer: vender\(x_1\) y comprar\(x_2\). Es natural leer las líneas discontinuas de la solución óptima de A y ver que dejar en el eje x significa vender, mientras que arriba en el eje y significa comprar.

Leer B es más complicado. B también tiene flechas, pero corren al revés de lo habitual porque leemos la gráfica de B desde la esquina noreste. B quiere comprar\(x_1\) y vender\(x_2\).

La dirección de la flecha indica la compra o venta. A pesar de que uno quiere comprar y el otro vender, la longitud de las flechas en la Figura 18.4 muestran que los planes no coinciden. La longitud de las flechas indican los montos a comprar y vender. Si las longitudes no son iguales, no estamos en equilibrio.

Revisamos las decisiones de compra y venta de B con más cuidado, para asegurarnos de que no haya confusión. B quiere comprar 20 unidades de buena 1. De su dotación inicial de 5 unidades, quiere moverse a la izquierda por el eje superior, lo que significa adquirir más\(x_1\), hasta terminar con 25 unidades. Por otro lado, quiere vender\(13 \frac{1}{3}\) unidades de bien 2, moviéndose hacia arriba por el eje derecho lo que significa que está reduciendo su cantidad deseada de\(x_2\).

Si te acostumbras a dibujar líneas discontinuas en una caja Edgeworth, ya sea en una hoja de papel o insertando formas de líneas discontinuas en Excel o Word, desde la solución óptima de A y B, aumentas enormemente tus posibilidades de leer el gráfico correctamente. Esas líneas discontinuas son una señal visual que te recuerda leer A desde la parte inferior izquierda y B desde la parte superior derecha.

PASO Desplácese hacia abajo debajo de la Caja Edgeworth para ver dos gráficas de oferta y demanda.

Estos son los mercados de equilibrio parcial para los dos bienes. Bueno 1 muestra un desabasto, con precio por debajo de la intersección de la oferta y la demanda. Bueno 2 tiene la demanda y la oferta invertidas de la exhibición habitual debido a que el precio en el eje y es\(p_1/p_2\). Hay un excedente de\(x_2\) at\(p_1/p_2 = \frac{2}{3}\).

Ambos mercados se ajustan simultáneamente. Sabemos que hay una presión al alza por el\(p_1\) desabasto y una presión\(p_2\) a la baja sobre el excedente. Esto hará que la relación precio suba y el vector de precios se volverá más empinado.

PASO Usa la barra de desplazamiento (sobre las celdas G15 y H15) para ver cómo afectan los cambios de precio a la caja. Establezca la relación precio en 1.5.

La hoja de cálculo hace la mayor parte del trabajo duro por ti. Las soluciones óptimas de A y B se calculan instantáneamente. Las celdas de posición de mercado reflejan inmediatamente la posición de los mercados para cada bien a los nuevos precios (donde bueno 1 es una vez y media más caro que bueno 2).

El Edgeworth Box es un gráfico en vivo que refleja el nuevo vector de precios. Demuestra que hemos sobrepasado el vector de precios de equilibrio porque ahora tenemos un superávit de bueno 1 y un desabasto de bueno 2.

PASO Practica la lectura de la caja Edgeworth. Con\(\frac{p_1}{p_2} = 1.5\), usa la gráfica para leer las cantidades que A y B quieren comprar y vender. Calcular el excedente y el desabasto de cada bien solo de la caja.

Verifica (usando las celdas de la parte Posición de Mercado de la hoja) que tus respuestas son correctas. Mire las gráficas debajo de la Caja Edgeworth para asegurarse de comprender que la Caja Edgeworth transmite la misma información sobre la posición de cada mercado.

PASO Juega con el vector precio, ajustando la barra de desplazamiento para establecer diferentes relaciones de precio e interpretando cómo responderán los consumidores a cada relación de precio usando la Caja Edgeworth.

A medida que rotas el vector de precio, eres el subastador walrasiano. Estás llamando a los precios y los dos consumidores están reaccionando a ellos. Cuanto más practiques leyendo la Caja Edgeworth, más cómodo te pondrás con ella.

A medida que ajusta la relación precio, el vector de precios oscila de un lado a otro. Siempre gira alrededor de la dotación inicial (que cambiaría si y solo si cambiara alguno de los cuatro valores iniciales de los parámetros de dotación). El proceso de tatonnement es como responde el mercado a desabastos y excedentes cambiando los precios de tal manera que se reducen los excedentes y desabastos, hasta que se eliminan por completo.

Por supuesto, no hay subastador en el mundo real, pero la presión de precios por los excedentes y la escasez son bastante reales. Nuestro modelo capta estas presiones por la ficción del subastador cambiando los precios en respuesta al desequilibrio en los dos mercados.

Equilibrio General

Se ha visto cómo la escasez y los excedentes empujan la línea de precios de un lado a otro, balanceándose alrededor del punto de dotación inicial.

Sabemos que el equilibrio significa que no hay tendencia al cambio. Aplicamos esta definición de equilibrio a este modelo particular: cuando no\(\frac{p_1}{p_2}\) tiene tendencia a cambiar, sabemos que nos hemos asentado a la solución de equilibrio. La solución de equilibrio generada por el mercado nos dice cuánto\(x_1\) y\(x_2\) cada consumidor terminará con si se usa el mercado y cuánto quiere comprar y vender cada consumidor de cada bien.

PASO Utilice la barra de desplazamiento para encontrar el vector de precio de equilibrio.

La solución de equilibrio en un Modelo de Intercambio Puro de Equilibrio General es una gráfica de economía canónica que se reproduce como Figura 18.5. Si tu pantalla no se parece a esta gráfica, establece la relación precio en 1.

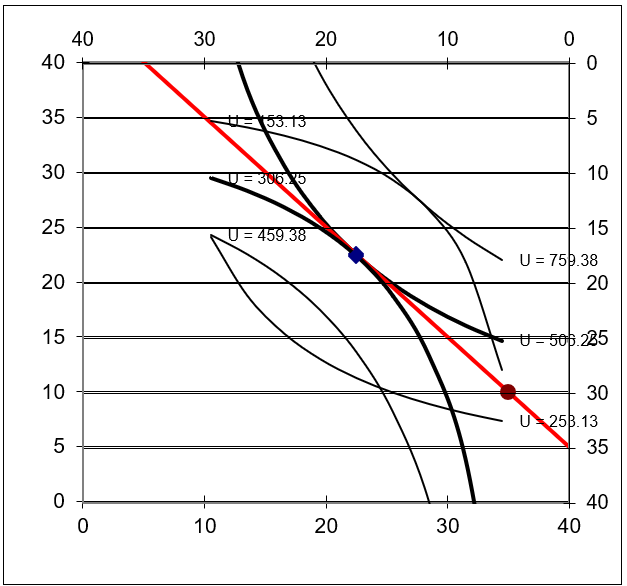
Figura 18.5: La gráfica canónica del equilibrio general.

Fuente: EdgeworthBoxGE.xls! EdgeWorthBox1 con\(\frac{p_1}{p_2}=1\).

Como muestra claramente la Figura 18.5, cuando se alcanza la posición de equilibrio, la solución óptima de ambos consumidores se encuentra en el mismo punto. Esto elimina todas las carencias y excedentes (como se muestra en las gráficas de oferta y demanda debajo de la Caja Edgeworth) por lo que la relación precio no tiene tendencia a cambiar.

El punto único de la caja Edgeworth representa una solución mutuamente compatible para ambos consumidores y es el sello distintivo de una solución de equilibrio general. El punto único es similar a la intersección de la oferta y la demanda en un análisis de equilibrio parcial.

Nuestro modelo de equilibrio general muestra cómo el mercado es un mecanismo de asignación. Redistribuirá las dotaciones iniciales de los dos consumidores mediante el uso de precios hasta que se establezca a una posición donde los planes coincidan y las fuerzas en el modelo estén en equilibrio.

Observe, sin embargo, que los dos consumidores no obtienen cantidades iguales de los dos bienes. ¿Por qué A termina con más? Porque A empezó más rico. En el vector de precios de equilibrio, el mercado valora la dotación de A en 45 dólares y las B's en 35 dólares. La teoría del equilibrio general no pregunta por qué A es más rico. Se necesita la dotación inicial como se le dio.

Ley de Walras

León Walras es el padre de la Teoría del Equilibrio General. La ley que lleva su nombre establece lo siguiente: El valor del exceso de demanda agregada es idénticamente cero.

Usando la Ley de Walras, podemos deducir el siguiente resultado lógico: Si\(n–1\) los mercados están en equilibrio, entonces el último mercado debe estar en equilibrio.

Una demostración concreta de la Ley Walras es la mejor manera de entender lo que significa.

PASO Con\(p_1 = 1\) (en la solución de equilibrio), cambiar\(p_2\) (celda H17) a 2. Encuentra el equilibrio\(p_1\).

El equilibrio\(p_1\) es ahora 2. Esto demuestra que, sin importar el valor de\(p_2\), la solución de equilibrio se encontrará cuando sea\(\frac{p_1}{p_2}\) igual a uno.

Así, parece que aquí hay dos variables endógenas,\(p_1\) y\(p_2\), pero en realidad solo hay una variable endógena,\(\frac{p_1}{p_2}\). Esta es la idea detrás de la Ley de Walras y por qué podemos encontrar el equilibrio en ambos mercados variando solamente\(p_1\).

PASO Haga clic en el botón. Desplácese hacia la derecha hasta la celda V5 y haga clic en el botón para revelar los cálculos que demuestran la Ley de Walras en acción.

Aunque los dos mercados no están en equilibrio, la suma del valor de las demandas netas agregadas en la celda Y11 es cero. Observa las fórmulas de celda en la fila 11 para ver cómo se calculan.

PASO Cambiar\(p_1\) (a través de la barra de desplazamiento) y notar que no importa el precio, la suma del valor de la demanda neta agregada es siempre cero.

Una implicación directa de la Ley Walras es que en un sistema de equilibrio general con n bienes, no tenemos que encontrar n precios. Si\(n - 1\) los mercados están en equilibrio, el último automáticamente tiene que estar en equilibrio.

Es por ello que en realidad solo tenemos una única variable endógena, la relación precio, en el caso de dos buenos. Todo lo que importa es el precio relativo, no los dos precios individuales. Con n bienes, un bien sería el numerario (históricamente, el oro ha jugado ese papel) y todos los demás bienes serían valorados en términos del numerario.

Estática comparada con la caja Edgeworth

Habiendo encontrado la solución de equilibrio inicial, podríamos perseguir una variedad de experimentos estáticos comparativos, impactando una variable exógena y rastreando cómo responde la solución de equilibrio (de diversas variables endógenas).

PASO Haga clic en el botón y luego establezca cA (celda B21) en 2. ¿Qué pasó con las curvas de indiferencia de A y la solución óptima?

Con curvas de indiferencia más pronunciadas (ya que A le gusta el 1 bueno más que antes), el nuevo punto de tangencia de A está bastante cerca de la dotación inicial. Esto significa que A quiere vender poco\(x_1\). Puedes desplazarte hacia abajo para ver cómo han cambiado las gráficas de equilibrio parcialla tabla de\(x_1\) confirma que tenemos un gran desabasto.

PASO ¿Dónde está la nueva solución de equilibrio? Si decide usar Solver para responder a esta pregunta, haga la celda de destino H15 porque esa es la celda a la que está afectando la barra de desplazamiento. De esta manera no destruirás la fórmula en la celda H16.

Debe encontrar una nueva solución de equilibrio a una relación de precio relativo de aproximadamente 1.53. Aproximadamente se intercambiarán 7.3 unidades del bien 1 y se intercambiarán 11.8 unidades de bien 2.

Dos ideas avanzadas

En un sentido matemático, la Teoría del Equilibrio General es quizás el área más abstracta y sofisticada de la economía. Dos preguntas que se han estudiado intensamente involucran la existencia y la singularidad.

La cuestión de la existencia de una solución de equilibrio la planteó el propio Walras. El tema, dicho vagamente, es que no podemos estar seguros de que un sistema de equilibrio general con miles o millones de bienes individuales tenga un lugar donde todo el sistema esté en reposo. De hecho, desde un punto de vista intuitivo, dada la gran cantidad de productos, consumidores y empresas en una economía del mundo real, podríamos dudar de que exista una solución de equilibrio en absoluto.

Walras y otros teóricos tempranos pensaron que si el número de variables endógenas (incógnitas) equivalía al número de ecuaciones, entonces se garantizaba una solución. Esto no es así. Las pruebas de existencia en la década de 1950 utilizaron teoremas de punto fijo para probar rigurosamente las condiciones bajo las cuales se garantizaba la existencia de una solución de equilibrio. Los teoremas de punto fijo de Brouwer y Kakutani son ejemplos de este enfoque.

Muy ligado a la existencia está el problema de la singularidad de una solución de equilibrio general. Incluso si se demuestra que existe una solución de equilibrio (en un sentido matemático riguroso), la preocupación es que puede haber múltiples equilibrios en un sistema de equilibrio general. La investigación se ha centrado en qué supuestos deben invocarse para garantizar una única solución de equilibrio.

Las pruebas de existencia y singularidad están mucho más allá del alcance de este libro. Se basan en la topología y en conceptos matemáticos avanzados. Esta es otra forma de decir que nuestra presentación de la Caja Edgework y el equilibrio general en una economía de intercambio pura es introductoria y rudimentaria. La Teoría del Equilibrio General es un vasto océano y estamos remando cerca de la costa.

Asignación de mercado en una caja Edgeworth

La gráfica canónica de oferta y demanda se utiliza en el análisis de equilibrio parcial para encontrar la solución de equilibrio. El equilibrio general usa la Caja Edgeworth para hacer lo mismo.

Parece engorroso y tedioso al principio, pero, de hecho, es un ingenioso dispositivo gráfico. Al representar a dos consumidores simultáneamente, mientras comparten una restricción presupuestaria común (dado que enfrentan precios idénticos), la caja permite ver rápidamente si la economía cambiaria pura y bibuena está en equilibrio. También revela cómo los precios deben cambiar a medida que el sistema encuentra su camino hacia el equilibrio a través del proceso de tatonnement.

Si una economía de cambio pura se encuentra en un equilibrio general se puede determinar en un instante viendo si las soluciones óptimas de los dos consumidores son compatibles es decir, si hay un solo punto donde los dos consumidores quieren estar, dada la relación de precios existente.

Pero, ¿qué pasa con la asignación final de equilibrio generada por el mercado, cuáles son sus propiedades? Esta es una cuestión fundamental que lleva a las famosas condiciones de optimalidad de Pareto y al Primer Teorema Fundamental de la Economía del Bienestar. Se explica en la siguiente sección.

Si bien hemos utilizado métodos numéricos (implementando el problema en Excel) para analizar y encontrar la solución de equilibrio general, debe ser consciente de que también existen enfoques analíticos. Podríamos anotar las demandas de bienes por parte de cada consumidor e imponer la condición de equilibrio que\(Q_D=Q_S\) en cada mercado. Esto permitiría la solución del vector de precios de equilibrio con la ayuda del álgebra (y, tan pronto como salimos del mundo simple de dos o tres bienes, álgebra lineal).

Ejercicios

1. Usa las Herramientas de Dibujo de Word para dibujar tu propia Caja Edgeworth. Colocar la dotación inicial para que A tenga\(x_2\) más de\(x_1\).

2. Agrega un vector de precio a tu caja en la pregunta anterior que genere un desabasto de\(x_1\). Dibuja flechas a lo largo de\(x_1\) los ejes inferior y superior para mostrar la cantidad de\(x_1\) cada consumidor que quiere comprar o vender.

3. Utilice las Herramientas de Dibujo de Word para dibujar un gráfico de oferta y demanda para\(x_1\). Incluir una línea horizontal en la gráfica que muestre el precio actual de\(x_1\).

4. Agrega el vector de precio de equilibrio a tu gráfica de Edgeworth Box en la pregunta 1. Explique por qué este vector de precios es la solución de equilibrio.

   Pista: Agrega curvas de indiferencia a tu gráfica para apoyar tu explicación.

Referencias

El epígrafe es de la página 11 de Umberto Ricci, “Pareto y la Economía Pura”, The Review of Economic Studies, Vol. 1, No. 1 (octubre de 1933), pp. 3—21, www.jstor.org/stable/2967433. Puede obtener más información sobre Walras, Pareto y la Escuela de Lausana visitando el sitio web de Historia del Pensamiento Económico en www.hetwebsite.net/het/.

Quizás ningún área de la economía es matemáticamente sofisticada e intensa como la Teoría del Equilibrio General. Siempre ha habido desacuerdo entre los economistas respecto al uso y la necesidad de las matemáticas en la economía. Pareto se burló de los economistas literarios y el uso de las matemáticas como arma continúa hoy en día.

Akerlof dice que los economistas solo valoran “duro” e ignoran las preguntas “blandas” por lo que la disciplina sofoca la investigación sobre temas que no pueden ser respondidos con herramientas y modelos formales. Ver George Akerlof (2020), "Los pecados de omisión y la práctica de la economía”, https://doi.org/10.1257/jel.20191573, 58 (2), 405—418, doi.org/10.1257/jel.20191573.

Roy Weintraub rastrea la influencia de las matemáticas en la economía en How Economics Become a Mathematical Science, publicado en 2002. Para la conexión entre economía y física, véase Phil Mirowski, More Heat than Light, publicado en 1989.