3.1: Continuidad de una función

Última actualización

30 oct 2022
Guardar como PDF
- 3: Límites - Continuidad
- 3.2: Continuidad en un Punto, Prueba de Continuidad, Tipos de Discontinuidad

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

La continuidad de una función está relacionada con la noción conceptual de una función que no tiene interrupciones ni saltos repentinos ya que la variable independiente toma todos los valores en algún intervalo. No hay brechas de alcance, ni saltos repentinos sobre el dominio de interés. Con esto en mente, vea si puede determinar cuál de los siguientes podría considerarse para representar una función continua:

variación diaria de la temperatura exterior
peso de un carro ya que se cargan bolsas de arena de 10 lb en él
la subida y bajada del nivel de un reservorio de agua
la cantidad de dinero recaudado en una sala de cine para una exhibición específica.

Continuidad

La continuidad de una función es conceptualmente la característica de una curva de función que tiene los valores del rango “flujo” continuamente sin interrupción durante algún intervalo, como si nunca tuviera que levantar el lápiz del papel mientras dibujaba la curva. Esta noción intuitiva necesita ser formalizada matemáticamente.

Considera la gráfica de la función f (x) =x ². La función se define para cualquier valor real de la variable independiente.

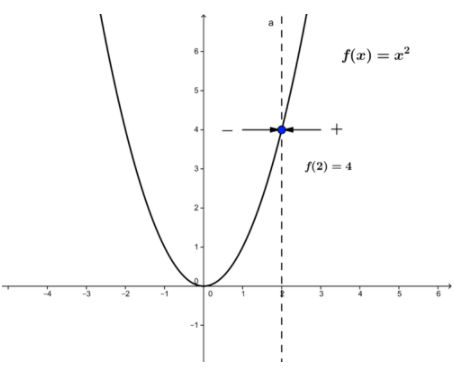
Screen Shot 2020-09-22 at 6.50.45 PM.png

Fundación CK-12 - CC BY-NC-SA

Por ejemplo, para x=2 la función tiene el valor f (2) =4. Observe que a medida que x se acerca al valor 2 desde la izquierda o la derecha, el valor de la función se acerca a 4, i.e.

$\lim _{x \rightarrow 2} f(x)=f(2)=4$

Conceptualmente, aplicando los límites unilaterales izquierdo y derecho a medida que x se acercaba a 2, resultó en el mismo valor, el valor de la función en x=2.

Los resultados anteriores ilustran las propiedades clave de una función continua. Se formalizan en la siguiente definición que proporciona una prueba para determinar cuándo tenemos una función continua.

La función f (x) es continua en x=a si se mantienen todas las siguientes condiciones:

Screen Shot 2020-09-22 at 6.53.48 PM.png

Tenga en cuenta que es posible tener funciones donde se cumplen dos de estas condiciones pero la tercera no. Cuando una función no es continua en x=a, entonces es discontinua en a, y a es un punto de discontinuidad.

Considere la función por partes

\ [f (x) =\ left\ {\ begin {array} {l}
x,\ text {if} x\ neq 1\\
3,\ text {if} x=1
\ end {array}\ right.\]

con la gráfica que se muestra a continuación.

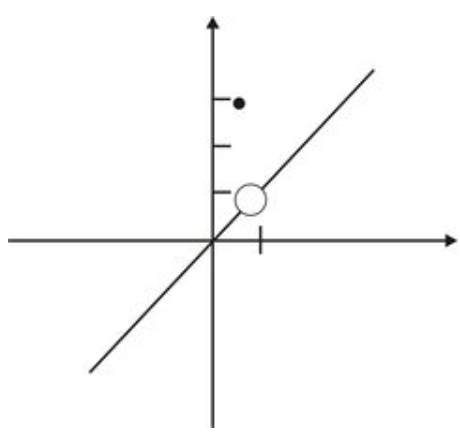
Screen Shot 2020-09-22 at 7.01.11 PM.png

Fundación CK-12 - CC BY-NC-SA

En este ejemplo, tenemos

$\lim _{x \rightarrow 1} f(x)$

¡existe! El valor x=1 está en el dominio de f (x), pero

$\lim _{x \rightarrow 1} f(x) \neq f(1)$

Por lo tanto, la función no es continua a x=1.

Este es un ejemplo de una discontinuidad removible, es decir, una discontinuidad en la que existe el límite de la función pero no es igual al valor de la función en ese punto.

Considere la siguiente función:

$f(x)=\frac{(x+1)}{\left(x^{2}-1\right)}$

¿Hay alguna discontinuidad?

Sabemos por nuestro estudio de dominios que para que se defina la función, debemos tener x≠ −1,1. Sin embargo, cuando generamos la gráfica de la función (usando la ventana de visualización estándar), obtenemos la siguiente imagen que parece estar definida en x=−1:

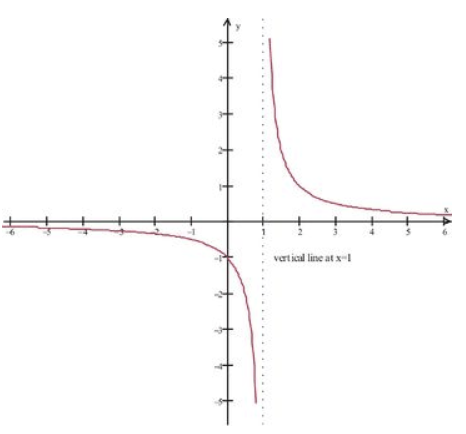
Screen Shot 2020-09-22 at 7.09.17 PM.png

Fundación CK-12 - CC BY-NC-SA

La aparente contradicción se debe a que nuestra función original tenía x+1 como factor común en el numerador y denominador, lo que canceló y nos dio una imagen que parece ser la gráfica de

$f(x)=\frac{1}{(x-1)}$

Pero lo que realmente tenemos es la función original,

$f(x)=\frac{(x+1)}{\left(x^{2}-1\right)}$

que sabemos no está definido en x=−1. En x=−1, tenemos un agujero en la gráfica, o una discontinuidad de la función en x=−1. Es decir, la función se define para todos los demás valores x cercanos a x=−1.

Además, a x=1 los valores de la función van a ±∞ dependiendo de qué lado de x=1 se use. Los límites unilaterales derecho e izquierdo no serán los mismos, y la función es discontinua en x=1. La discontinuidad en x=1 se denomina discontinuidad infinita y se asocia con la asíntota vertical x=1.

Hablando en voz baja, si tuviéramos que dibujar a mano la gráfica, tendríamos que sacar nuestro lápiz de la página cuando lleguemos a este agujero, dejando un hueco en la gráfica como se indica:

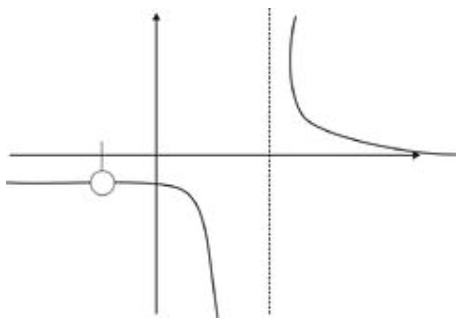
Screen Shot 2020-09-22 at 7.11.35 PM.png

Fundación CK-12 - CC BY-NC-SA

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó cuál de los siguientes podría considerarse que representa una función continua:

variación diaria de la temperatura exterior
peso de un carro ya que se cargan bolsas de arena de 10 lb
la subida y bajada del nivel de agua en un embalse
la cantidad de dinero recaudado en una sala de cine para una exhibición específica

La variación diaria de la temperatura exterior podría considerarse una función continua del tiempo, ya que todos los valores de temperatura ocurren en el rango de variación.

El peso de un carro ya que se cargan bolsas de arena de 10 lb no se consideraría una función continua del número de bolsas porque solo son posibles números enteros de bolsas y el peso total cambia en incrementos de 10 lb, por lo que hay huecos.

La subida y caída del nivel de agua en un embalse podría considerar una función continua del tiempo porque todos los niveles ocurren en el rango de variación.

La cantidad de dinero recaudado en una sala de cine para una presentación específica no se consideraría una función continua ya que el número de personas que compran y el precio por boleto son enteros por lo que solo son posibles ciertos montos totales en dólares.

Ejemplo 2

Encuentre un valor de k que haga que la siguiente función sea continua:

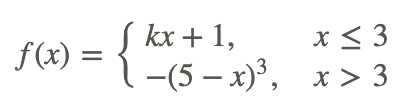
Screen Shot 2020-09-22 at 7.12.26 PM.png

Si f (x) debe considerarse continuo en todas partes, debe ser continuo en x=3. Esto significa que:

Screen Shot 2020-09-22 at 7.14.33 PM.png

Entonces

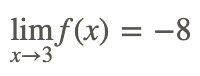
Screen Shot 2020-09-22 at 7.14.53 PM.png

Con el resultado anterior, tenemos

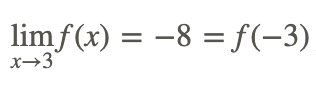
Screen Shot 2020-09-22 a las 7.15.16 PM.png

Por lo tanto, la función

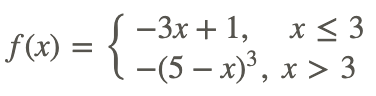
Screen Shot 2020-09-22 at 7.16.32 PM.png

es continuo a x=3.

Ejemplo 3

Recordemos nuestra función básica de raíz cuadrada, f (x) =x ^0.5, que se muestra a continuación. ¿Es continuo a x=0?

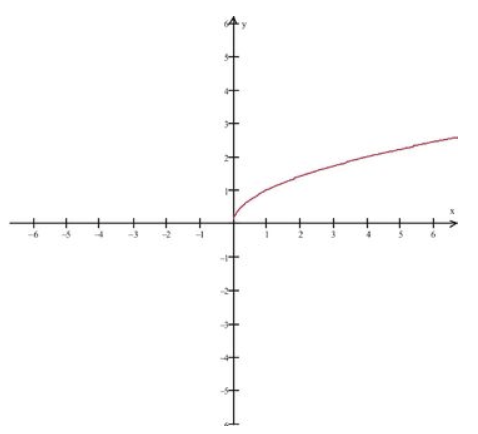
Screen Shot 2020-09-22 at 7.17.07 PM.png

Fundación CK-12 - CC BY-NC-SA

Como el dominio de f (x) =x ^0.5 es x≥0, vemos que

$\lim _{x \rightarrow 0} \sqrt{x}$

no existe. Específicamente, no podemos encontrar intervalos abiertos alrededor $x=0$ que satisfagan la definición de límite. Por lo tanto, la función no es continua en $x=0$ . Sin embargo sí observamos que a medida que nos acercamos a x=0 desde el lado derecho, vemos los valores sucesivos tendiendo hacia $x=0$ .

Revisar

Screen Shot 2020-09-22 a las 8.20.18 PM.png

Screen Shot 2020-09-22 a las 8.20.36 PM.png

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.9.

vocabulario

Término	Definición
Continuo	La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido.
Función continua	Una función continua es una función sin roturas ni huecos. Contiene un número infinito e incontable de valores.
discontinuidades	Los puntos de discontinuidad para una función son los valores de entrada de la función donde la función es discontinua.
discontinuo	Una función es discontinua si la función presenta roturas o agujeros cuando se grafica.
discontinuo en un punto	Una función es discontinua en un punto a si la función no está definida en x=a.
Discontinuidades infinitas	Las discontinuidades infinitas ocurren cuando una función tiene una asíntota vertical en uno o ambos lados. Esto sucederá cuando un factor en el denominador de la función sea cero.
Discontinuidad infinita	Las discontinuidades infinitas ocurren cuando una función tiene una asíntota vertical en uno o ambos lados. Esto sucederá cuando un factor en el denominador de la función sea cero.
puntos de discontinuidad	Los puntos de discontinuidad para una función son los valores de entrada de la función donde la función es discontinua.
Discontinuidades removibles	Las discontinuidades removibles también se conocen como agujeros. Ocurren cuando los factores pueden ser cancelados algebraicamente a partir de funciones racionales.
Discontinuidad removible	Las discontinuidades removibles también se conocen como agujeros. Ocurren cuando los factores pueden ser cancelados algebraicamente a partir de funciones racionales.

Recursos adicionales

PLIX: Juega, aprende, interactúa, explora - Continuidad

Video: Continuidad usando límites

Práctica: Continuidad de una función

Mundo real: ADN mitocondrial

Search

Text Color

Text Size

Margin Size

Font Type

Continuidad

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Revisar

Reseña (Respuestas)

vocabulario

Recursos adicionales

Support Center

How can we help?