9.3: Suma de área

Encontrar el área bajo la curva de una función, f (x), es uno de los problemas centrales que surge en Cálculo. Ya sabes cómo calcular el área de algunas formas simples de curvas de función usando fórmulas geométricas, y a veces puedes usar rápidamente estos métodos. Pero, ¿qué harías si las curvas de función fueran más complejas? El enfoque clave del cálculo es tomar un método simple, aplicarlo a pequeña escala, y luego llevarlo al límite al infinito.

Para conocer la idea de encontrar el área bajo una curva, haga lo siguiente antes de ir más allá: tome una curva de parábola simple (cóncava hacia arriba y positiva), divida un intervalo en el eje x en un número de subintervalos iguales y dibuje un rectángulo en cada subintervalo que intersecta la parábola. La suma de los rectángulos sería una estimación del área. ¿Cuántos tipos diferentes de intersecciones puede hacer un rectángulo con la parábola? ¿Se puede decir algo sobre cómo la intersección bajo o sobre estima el área debajo de la curva? ¿Ves que cuantos más rectángulos se usen para un intervalo dado, mejor será la estimación?

---

Sumas de Riemann

Para funciones simples como f (x) =c (c>0), o f (x) =cx (c es una constante >0) en algún intervalo [0, x ₀], podemos usar geometría simple para obtener el área debajo de cada curva (intente confirmarlo por su cuenta):

1. Para f (x) =c (c>0); el área A es la de un rectángulo simple, a=Cx0.
2. Para f (x) =cx (c>0); el área A es la de un triángulo simple,\( A=\frac{1}{2}x_0(cx_0)=c\frac{x_0^2}{2} \nonumber\).

¿Cómo se puede determinar el área para funciones más complejas?

Consideremos nuestra función cuadrática básica\( f(x)=x^2 \nonumber\). Supongamos que estamos interesados en encontrar el área, A, bajo la curva de x=0 a x=1. El área de la que estamos hablando es el espacio rayado cruzado bajo la curva que se muestra a continuación.

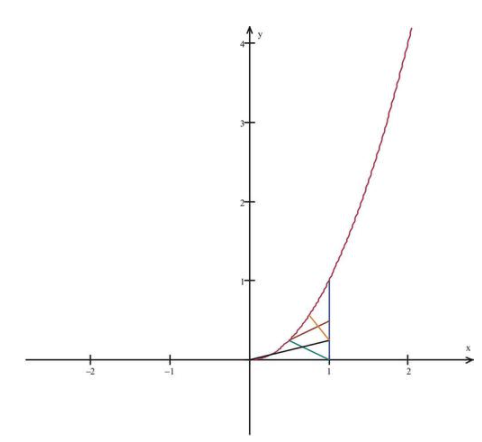
CC BY-NC-SA

Una forma de estimar el área bajo la curva es calcular el área del cuadrado que tiene una esquina en (1, 1) como se muestra a continuación, y luego tomar la mitad.

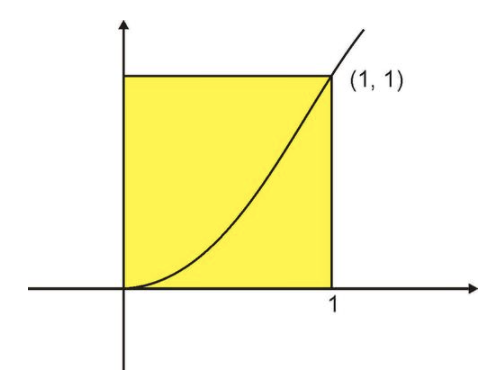
CC BY-NC-SA

Esto le da un área\( A=\frac{1}{2} \nonumber\). Esta es una buena primera estimación del área; se mostrará que la respuesta exacta es\( A=\frac{1}{3} \nonumber\).

¿Cómo podemos hacer una mejor estimación? ¿Qué tal dividir el intervalo x de x=0 a x=1 en múltiples subintervalos de igual anchura?

Veamos los problemas que cada uno tiene más subintervalos que el anterior.

4 subintervalos iguales:

Comience usando cuatro subintervalos como se indica:

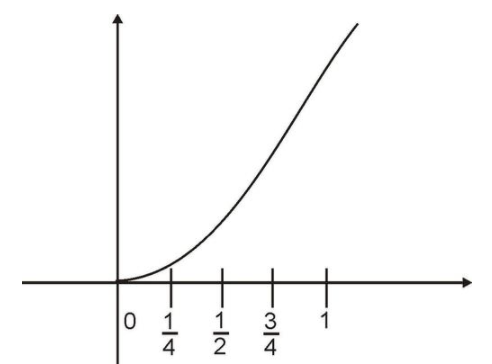
Ahora construiremos cuatro rectángulos que servirán de base para nuestra aproximación del área. Los subintervalos servirán como el ancho de los rectángulos. Tomaremos la longitud de cada rectángulo para que sea el valor máximo de la función en el subintervalo. (También podríamos elegir el valor mínimo o de punto medio de la función en el subintervalo.)

De ahí que obtengamos la siguiente figura:

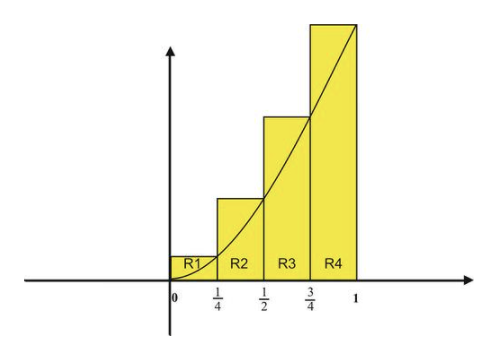
Si llamamos a los rectángulos R1−R4, de izquierda a derecha, entonces tenemos las áreas

Encontrar el área bajo la curva de una función, f (x), es uno de los problemas centrales que surge en Cálculo. Ya sabes cómo calcular el área de algunas formas simples de curvas de función usando fórmulas geométricas, y a veces puedes usar rápidamente estos métodos. Pero, ¿qué harías si las curvas de función fueran más complejas? El enfoque clave del cálculo es tomar un método simple, aplicarlo a pequeña escala, y luego llevarlo al límite al infinito.

Para conocer la idea de encontrar el área bajo una curva, haga lo siguiente antes de ir más allá: tome una curva de parábola simple (cóncava hacia arriba y positiva), divida un intervalo en el eje x en un número de subintervalos iguales y dibuje un rectángulo en cada subintervalo que intersecta la parábola. La suma de los rectángulos sería una estimación del área. ¿Cuántos tipos diferentes de intersecciones puede hacer un rectángulo con la parábola? ¿Se puede decir algo sobre cómo la intersección bajo o sobre estima el área debajo de la curva? ¿Ves que cuantos más rectángulos se usen para un intervalo dado, mejor será la estimación?

8 Subintervalos iguales:

f dividimos el intervalo en 8 subintervalos iguales, el ancho de cada rectángulo es ahora w=18.

La estimación del área ahora se convierte en:

\[ A≈R_1+R_2+R_3+R_4+R_5+R_6+R_7+R_8 \nonumber\]

\[ ≈ \sum_{i=1}^8 R_i \nonumber\]Uso de la notación Sigma

\[ ≈\frac{1}{512}+\frac{4}{512}+\frac{9}{512}+\frac{16}{512}+\frac{25}{512}+\frac{36}{512}+\frac{49}{512}+\frac{64}{512} \nonumber\]

\[ ≈\frac{204}{512} \nonumber\]

\[ A≈0.3984 \nonumber\]

Tenga en cuenta que la notación Sigma\( (\sum_{i=1}^8 R_i) \nonumber\) utilizada anteriormente nos permite indicar la suma de las áreas de rectángulo individuales sin la necesidad de escribir todos los términos individuales. El símbolo sigma con estos índices nos dice cómo se etiquetan los rectángulos y cuántos términos hay en la suma.

Además, la suma de rectángulos que da la aproximación del área podría escribirse de la siguiente forma general:

\[ A≈R=\sum_{i=1}^n R_i= \sum_{i=1}^n f(w_i)(x_i−x_{i−1})=\sum_{i=1}^n f(w_i)Δx_i \nonumber\]

donde elegimos que el valor de n sea tan grande como queramos, wi sea cualquier valor de x en el intervalo\( (x_i−x_i−1)\nonumber\), y\( (x_i−x_i−1) \nonumber\) que sea el i-ésimo de n subintervalos (no necesariamente iguales) en el intervalo [a, b] en el que f se define. Este tipo de suma se llama suma de Riemann.

16 sub-intervalos iguales:

Si ahora dividimos el intervalo en 16 subintervalos iguales, el ancho de cada rectángulo es ahora\( w=\frac{1}{16} \nonumber\).

La estimación del área ahora se convierte en:

\[ A≈R_1+R_2+R_3+R_4+R_5+⋯+R_{16} \nonumber\]

\[ ≈\sum_{i=1}^{16} R_i \nonumber\]Uso de la notación Sigma

\[ ≈\frac{1}{4096}+\frac{4}{4096}+\frac{9}{4096}+⋯+\frac{196}{4096}+\frac{225}{4096}+\frac{256}{4096} \nonumber\]

\[ ≈\frac{1496}{4096} \nonumber\]

\[ A≈0.3652 \nonumber\]

Nuevamente, se ha utilizado la notación sigma para eliminar la necesidad de escribir todos los términos individuales.

La tabla da un resumen de los resultados estimados de área hasta el momento.

Área estimada bajo\( f(x)=x^2 \nonumber\) en el intervalo [0, 1]

Subintervalos	Estimación de área
1	1 (0.5)
4	0.4688
8	0.3984
16	0.3652

Intuitivamente, tenemos la sensación de que podemos mejorar la aproximación del área subdividiendo el intervalo de x=0 a x=1 en más y más sub-intervalos, creando así sucesivamente rectángulos cada vez más pequeños para refinar nuestras estimaciones.

Ahora estamos listos para formalizar el uso de sumas para computar áreas.

Primero, definimos las sumas inferior y superior:

Sea f una función delimitada en un intervalo cerrado [a, b] y\( P=[x_0,…,x_n] \nonumber\) la partición de [a, b] en n subintervalos.

Definir las sumas inferior y superior, respectivamente, sobre la partición P, por

\[ S(P)=\sum_{1}^{n} m_i(x_i−x_{i−1})=m_1(x_1−x_0)+m_2(x_2−x_1)++m_n(x_n−x_{n−1}) \nonumber\]

\[ T(P)= \sum_1^n M_i(x_i−x_{i−1})=M1_(x_1−x_0)+M_2(x_2−x_1)+…+M_n(x_n−x_{n−1}) \nonumber\]

donde mi es el valor mínimo de f en el intervalo de longitud\( x_i−x_{i−1} \nonumber\) y\( M_i \nonumber\) es el valor máximo de f en el intervalo de longitud\( x_i−x_{i−1} \nonumber\).

S (P) y T (P) son sumas de Riemann, donde mi y Mi son opciones particulares para wi en la formulación general de la suma de Riemann anterior.

A continuación, vincularemos el área bajo una curva con el límite de las sumas inferiores o superiores para un número cada vez mayor de subintervalos:

Sea f una función continua no negativa en un intervalo cerrado [a, b]. Sea P una partición de n subintervalos iguales sobre [a, b]. Entonces el área bajo la curva de f es el límite de las sumas superior e inferior, es decir

\[ A= \lim_{n \to +∞} S(P)= \lim_{n \to +∞}T(P) \nonumber\]

El siguiente problema muestra cómo podemos usar estas definiciones para encontrar el área bajo una curva.

Mostrar que el límite de suma superior para la función\( f(x)=x^2 \nonumber\), from\( x=0 \mbox{ to } x=x_0 \nonumber\), se acerca al valor\( A=\frac{x_0^3}{3} \nonumber\).

Que P sea una partición de n subintervalos iguales sobre\( [0,x_0] \nonumber\). Por definición tenemos

\[ T(P)= \sum{1}^{n} M_i(x_i−x_{i−1})=M_1(x_1−x_0)+M_2(x_2−x_1)+…+M_n(x_n−x_{n−1}) \nonumber\]

Cada rectángulo tendrá ancho\( \frac{x_0}{n} \nonumber\), de manera que la evaluación de T (P) es:\( T(P)= \sum_{1}^{n} M_i(x_i−x_{i−1}) \nonumber\)

\( = M_2(x_2−x_1)+…+M_n(x_n−x_{n−1}) \nonumber\)

\( =(\frac{x_0}{n})2\frac{x_0}{n}+(2\frac{x_0}{n})2\frac{x_0}{n}+…+(n\frac{x_0}{n})2\frac{x_0}{n} \nonumber\)Subintervalos de igual longitud.

\( =(\frac{x_0}{n})^2\frac{x_0}{n}(1^2+2^2+3^2+…+n^2) \nonumber\)

\( =(\frac{x_0}{n})^3(1^2+2^2+3^2+…+n^2) \nonumber\)

\( =(\frac{x_0^3}{n})^3(\frac{n(n+1)(2n+1)}{6}) \nonumber\)Hace uso de:\( \sum_{i=1}^{n} i^2=\frac{n(n+1)(2n+1)}{6} \nonumber\)

\( =(\frac{x_0^3}{6})(\frac{n(n+1)(2n+1)}{n^3}) \nonumber\)

\(=(\frac{x_0^3}{6})(1+\frac{1}{n})(2+\frac{1}{n}) \nonumber\)

Observe que:

\[ \lim_{n \to ∞} [(\frac{x_0^3}{6})(1+\frac{1}{n})(2+\frac{1}{n})]=(\frac{x_0^3}{6})⋅2=\frac{x_0^3}{3} \nonumber\]

El área, A, bajo la curva de la función\( f(x)=x^2 \nonumber\) from\( x=0 \mbox{ to } x=x_0 \nonumber\), se acerca al valor\( A=\frac{x_0^3}{3} \nonumber\). Tenga en cuenta que si x0=1, obtenemos el resultado A=13. Compare este valor con los resultados del problema anterior.

El mismo enfoque para determinar el área se puede utilizar con S (P), y arroja el mismo resultado,\( A = \frac{x_0^3}{3} \nonumber\).

---

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó sobre el uso de rectángulos para estimar el área bajo una curva. ¿Cuántos tipos diferentes de intersecciones puede hacer un rectángulo con la parábola? ¿Se puede decir algo sobre cómo la intersección bajo o sobre estima el área debajo de la curva? ¿Puedes ver que cuantos más rectángulos se usen (subintervalo menor) para un intervalo dado, mejor será la estimación del área?

Donde tu rectángulo se cruza con la parábola establece la altura del rectángulo, y solo depende del valor de x dentro del subintervalo: extremo izquierdo del rectángulo (comienzo del subintervalo), extremo derecho del rectángulo (final del subintervalo), o cualquier punto intermedio. Para esta parábola cóncava hacia arriba, deberías poder ver que usando un rectángulo del extremo izquierdo subestima el área debajo de la parábola; un rectángulo del extremo derecho sobreestima el área. Un rectángulo con altura en algún punto intermedio, digamos en el punto medio, podría sobreestimar una porción y subestimar una porción, es decir, proporcionar una mejor estimación del área.

Ejemplo 2

Utilice la definición límite de área para encontrar el área bajo la función f (x) =4−x de 1 a x=3.

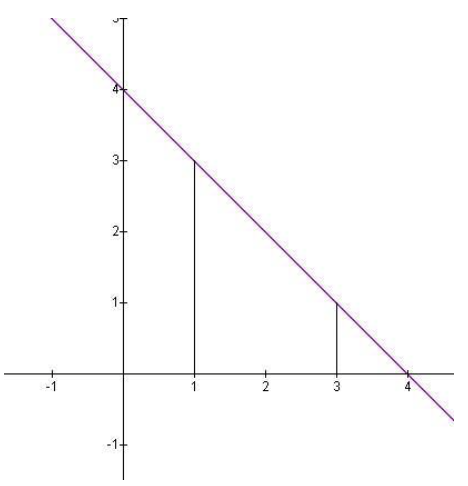
Si particionamos el intervalo [1,3] en n subintervalos iguales, entonces cada subintervalo tendrá longitud\( \frac{3−1}{n}=\frac{2}{n} \nonumber\), y altura 3−ix ya que i varía de 1 a n Así que tenemos\( △x=\frac{2}{n} \nonumber\) y

\( S(P)= \sum_1^n m_i(x_i−x_{i−1}) \nonumber\)Suma inferior usando el valor mínimo de función en cada subintervalo.

\( = \sum_1^n (3−i\frac{2}{n})\frac{2}{n} \nonumber\)

\( S(P)= \sum_1^n m_i(x_i−x_{i−1}) \nonumber\)Subintervalos de igual longitud.

\( = \sum_1^n (3⋅\frac{2}{n})− \sum_1^n i(\frac{2}{n})^2 \nonumber\)

\( =6−(\frac{2}{n})^2 \sum_1^n i \nonumber\)

\( =6−(\frac{2}{n})^2⋅(\frac{n(n+1)}{2}) \nonumber\)Hace uso de:

\( =6−2⋅(\frac{n(n+1)}{n^2}) \sum_{i=1}^n i=\frac{n(n+1)}{2} \nonumber\)

\( S(P)=6−2⋅(1+\frac{1}{n}) \nonumber\)

Observe que:

\[ \lim_{n \to ∞} [6−2⋅(1+\frac{1}{n})]=6−2=4 \nonumber\]

El área, A, bajo la curva de la función se acerca al valor A=4. El mismo enfoque se puede utilizar con S (P), dando el mismo resultado.

Por supuesto este ejemplo también puede resolverse con geometría simple. Se deja al lector confirmar que los dos métodos arrojan la misma área.

---

Revisar

Para #1 -3, encuentra S (P) y T (P) debajo de la partición P.

1. \( f(x)=1−x^2, P={0,12,1,32,2}  \nonumber\)
2. \( f(x)=2x^2, P={−1,−12,0,12,1}  \nonumber\)
3. \( f(x)=\frac{1}{x}, P={−4,−3,−2,−1} \nonumber\)
4. Considera f (x) =2−x de x=0 a x=2. Utilice Sumas de Riemann con cuatro subintervalos de igual longitud. Elija los puntos medios de cada subintervalo como los puntos de muestreo.
5. Repita el problema #1 usando geometría para calcular el área exacta de la región bajo la gráfica de f (x) =2−x de x=0 a x=2. (Pista: bosquejar un gráfico de la región y ver si puede calcular su área usando fórmulas de medición de área a partir de la geometría).
6. Repita el problema #4 usando la definición de la integral definida para calcular el área exacta de la región bajo la gráfica de f (x) =2−x de x=0 a x=2.
7. \( f(x)=x^2−x \nonumber\)de x=1 a x=4. Utilice Sumas de Riemann con cinco subintervalos de igual longitud. Elija el punto final izquierdo de cada subintervalo como los puntos de muestreo.
8. Repita el problema #7 usando la definición de la intergal definida para calcular el área exacta de la región bajo la gráfica\( f(x)=x^2−x \nonumber\) de x=1 a x=4.
9. Considerar\( f(x)=3x^2 \nonumber\). Calcular la suma de Riemann de f on [0, 1] bajo cada una de las siguientes situaciones. En cada caso, use el punto final correcto como los puntos de muestra.
   1. Dos sub-intervalos de igual longitud.
   2. Cinco sub-intervalos de igual longitud.
   3. Diez sub-intervalos de igual longitud.
   4. Con base en sus respuestas anteriores, intente adivinar el área exacta bajo la gráfica de f en [0, 1].
10. Considerar\( f(x)=e^x \nonumber\). Calcular la suma de Riemann de f on [0, 1] bajo cada una de las siguientes situaciones. En cada caso, use el punto final correcto como los puntos de muestra.
    1. Dos sub-intervalos de igual longitud.
    2. Cinco sub-intervalos de igual longitud.
    3. Diez sub-intervalos de igual longitud.
    4. Con base en sus respuestas anteriores, intente adivinar el área exacta bajo la gráfica de f en [0, 1].
11. Encuentra el área neta bajo la gráfica de\( f(x)=x^3−x \nonumber\); x=−1 a x=1. (Pista: bosquejar la gráfica y verificar si hay simetría.)
12. Encuentra el área total delimitada por la gráfica de\( f(x)=x^3−x \nonumber\) y el eje x, de a x=−1 a x=1.
13. Usa tus conocimientos de geometría para evaluar la integral definida:\( \int\limits_0^3 \sqrt{9−x^2}dx \nonumber\)

(Pista: establece\( y= \sqrt{9−x^2} \nonumber\) y cuadra ambos lados para ver si puedes reconocer la región a partir de la geometría.)

Para #14 -15, encuentra el área bajo la curva usando la definición límite de área.

14. f (x) =3x+5 de x=2 a x=6.
15. \( f(x)=x^2 \nonumber\)de x=1 a x=3.

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.4.

---

El vocabulario

Término	Definición
función acotada	Una función acotada es una función f (x) para la cual f (x) ≤M (M un número real) para todos los valores de x en el dominio.
suma inferior	Una suma inferior es una suma de Riemann que elige el valor mínimo de la función en cada subintervalo en la partición de un intervalo cerrado.
partición de un intervalo cerrado	Una partición de un intervalo cerrado es una descomposición de todo el intervalo en una serie de subintervalos contiguos.
notación sigma	La notación sigma también se conoce como notación de suma y es una forma de representar una suma de números. Es especialmente útil cuando los números tienen un patrón específico o tardarían demasiado en escribirse sin abreviar.
suma superior	Una suma superior es una suma de Riemann que elige el valor máximo de la función en cada subintervalo en la partición de un intervalo cerrado.

---

Recursos adicionales

PLIX - Juega, aprende, interactúa, explora: sumas de área: estimación con rectángulos

Video: Aproximación trapezoidal del área bajo la curva

Práctica: Sumas de área

Mundo real: llamándolo