9.2: Antiderivado
- Page ID
- 105930
Has pasado muchas lecciones aprendiendo sobre cómo encontrar la derivada, f′ (x), de una función f (x), y el proceso de diferenciación. No debería sorprender entonces que hubiera un nombre para la función f (x), o familia de funciones, que pueda generar f′ (x) cuando se diferencie: f (x) y f′ (x) son un par de funciones inversas, y f (x) se llama antiderivada de f′ (x). Antes de continuar con la lección, ¿intenta enumerar funciones que son pares antiderivados y derivados?
El Antíderivado
Empecemos e introduzcamos la idea de la antiderivada de una función.
Una función F (x) se denomina antiderivada de una función f si F′ (x) =f (x) para todo x en el dominio de f.
¿Cómo se usa esta definición?
Considera la función\( f(x)=3x^2 \nonumber\).
¿Se te ocurre una función F (x) tal que F′ (x) =f (x)? Deberías ser capaz de pensar en muchos de ellos.
Ya que diferenciamos F (x) para obtener f (x), vemos que\( F(x)=x^3+C \nonumber\) va a funcionar para cualquier constante C. Gráficamente, podemos pensar en el conjunto de todas las antiderivadas como transformaciones verticales de la gráfica de\( F(x)=x^3 \nonumber\). La figura muestra dos transformaciones de este tipo.
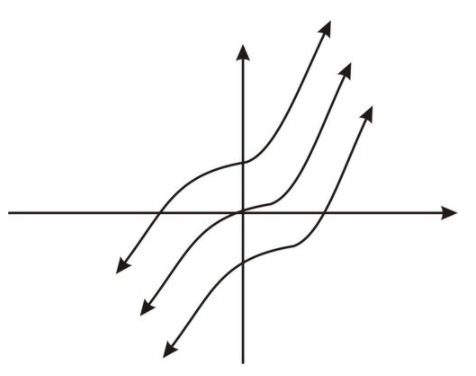
CC BY-NC-SA
Con nuestra definición y ejemplo inicial, ahora buscamos formalizar la definición y desarrollar algunas reglas útiles con fines computacionales, y comenzar a ver algunas aplicaciones.
Introducción a Integrales Indefinidas
El proceso de búsqueda de antiderivados se denomina antidiferenciación, más comúnmente denominado integración. Así es como se indica la integración y cómo funciona:
F′ (x) =f (x)... Comienza con la ecuación diferencial que representa la definición de la antiderivada
\( \int F′(x)dx=\int f(x)dx \nonumber\)... Invoque la operación de integración (antidiferenciación) usando el símbolo especial ∫.
\( F(x)+C= \int f(x)dx \nonumber\)... Obtener el antiderivado F (x) y una constante de integración, C.
\( \int f(x)dx=F(x)+C \nonumber\)... Tenga en cuenta que si diferenciamos ambos lados, recuperamos la ecuación original:
\[ \frac{d}{dx}[ \int f(x)dx]=f(x)=\frac{d}{dx}[F(x)+C]=F′(x) \nonumber\]
Nos referimos a f (x) dx como “la integral indefinida de f (x) con respecto a x”. La función f (x) se llama integrando y la constante C se llama la constante de integración . Finalmente el símbolo dx indica que vamos a integrar con respecto a x.
Usando esta notación, resumiremos el último ejemplo de la siguiente manera:
\[ \int 3x^2dx=x^3+C \nonumber\]
Ahora, considere la función f (x) =cosx
¿Se te ocurre una función F (x) tal que F′ (x) =f (x)?
Si dijiste F (x) =SINX+C estarías en lo correcto y así es como se escribiría esto.
f (x) =F′ (x). Comienza con la ecuación diferencial que representa la definición de la antiderivada
COSx=F′ (x). Sustituto de f (x)
\( \int cosx dx= \int F′(x)dx \nonumber\)... Invoque la operación de integración (antidiferenciación) usando el símbolo especial ∫.
\( \int cosx dx=F(x)+C \nonumber\)... Obtener el antiderivado F (x) y una constante de integración, C.
\( \int cosx dx=sinx+C \nonumber\)... Sabemos F (x) =sinx porque si diferenciamos ambos lados, recuperamos la ecuación original.
Hemos visto las derivadas de una serie de funciones a través de los conceptos de cálculo y podemos armar una lista de funciones y sus antiderivadas como se muestra a continuación.
|
Función f (x) |
Antiderivado\( /int f(x)dx=F(x)+C \nonumber\) |
| 1 | x+C |
| x |
\( \frac{x^2}{2}+C \nonumber\) |
|
\( x^2 \nonumber\) |
\( \frac{x^3}{3}+C \nonumber\) |
|
\( x^n,\nonumber\) n−1 |
\( \frac{x^{n+1}}{n+1}+C \nonumber\) |
|
\( \frac{1}{x} \nonumber\) |
\( lnx+C \nonumber\) |
|
sinx |
−COSX+C |
|
cosx |
Sinx+C |
|
\( sec^2x \nonumber\) |
Tanx+C |
|
\( csc^2x \nonumber\) |
−CoTx+C |
|
secxtanx |
Secx+C |
|
cscxcotx |
−CSCX+C |
|
\( e^x \nonumber\) |
\( e^x+C \nonumber\) |
|
\( b^x \nonumber\) b>0 |
\( \frac{b^x}{lnb}+C \nonumber\) |
|
\( \frac{1}{xlnb} \nonumber\) |
\( log_bx+C \nonumber\) |
Al igual que con la diferenciación, existen varias reglas para tratar la suma y diferencia de funciones integrables.
Reglas básicas de integración
Si f y g son funciones integrables, y C es una constante, entonces:
\[ \int [f(x)+g(x)]dx= \int f(x)dx+ \int g(x)dx \nonumber\],
\[ \int [f(x)−g(x)]dx= \int f(x)dx− \int g(x)dx \nonumber\],
\[ \int [Cf(x)]dx=C \int f(x)dx \nonumber\]
Calcular la siguiente integral indefinida.
\[ \int [2x^3+3x^2−1x]dx \nonumber\]
Usando nuestras reglas tenemos
\[ \int [2x^3+3x^2−1x]dx=2 \int x^3dx+3 \int \frac{1}{x^2}dx− \int \frac{1}{x}dx \nonumber\]
\[ =2(\frac{x^4}{4})+3(\frac{x^{−1}}{−1})−lnx+C \nonumber\]
\[ =\frac{x^4}{2}−\frac{3}{x}−lnx+C \nonumber\].
Tenga en cuenta que a veces nuestras reglas necesitan ser modificadas ligeramente debido a operaciones con constantes.
Ejemplos
Ejemplo 1
Anteriormente, se le pidió que intentara enumerar funciones que son pares antiderivados y derivados. Al hacerlo estás presentando los resultados de las operaciones de diferenciación e integración. Si todo lo que hiciste fue enumerar la función que se está diferenciando como la antiderivada, esto es correcto. A estas alturas ya te has dado cuenta de que existe una familia de antiderivados entre los que podrías haber elegido, cada uno diferente por una constante de integración.
Ejemplo 2
Calcular la siguiente integral indefinida:
\[ \int e^{3x}dx \nonumber\].
Primero notamos que nuestra regla para integrar funciones exponenciales no funciona aquí ya que ddxe3x=3e3x. Sin embargo, si recordamos dividir la función original por la constante entonces obtenemos la antiderivada correcta y tenemos
\[ \int e^{3x}dx=\frac{e^{3x}}{3}+C \nonumber\].
Ahora podemos reafirmar la regla de una forma más general como
\[ \int e^{kx}dx= \frac{e^{kx}}{3}+C \nonumber\].
Revisar
Para #1 -6, encuentra una antiderivada de la función
- \( f(x)=1−3x^2−6x \nonumber\)
- \( f(x)=x−x^\{frac{2}{3}} \nonumber\)
- \( f(x)=(2x+1)^{\frac{1}{5}} \nonumber\)
- \( f(x)=cosx−x \nonumber\)
- \( f(x)=x^5−7x^2+2 \nonumber\)
- \(f(x)=e^{−2x}+e^x \nonumber\)
Para #7 -12, encuentra la integral indefinida
- \ (\ int (2+\ sqrt {5}) dx\ nonumber\]
- \( \int 2(x−3)^3dx \nonumber\)
- \( \int (x^2⋅x^\frac{1}{3})dx \nonumber\)
- \( \int (x+\frac{1}{x^4\sqrt{x}})dx \nonumber\)
- \( (cosx+2sinx)dx \nonumber\)
- \( \int 2sinxcosxdx \nonumber\)
- Resolver la ecuación diferencial\( f′(x)=4x^3−3x^2+x−3 \nonumber\).
- Encuentra la antiderivada F (x) de la función\( f(x)=2e^{2x}+x−2 \nonumber\) que satisface F (0) =5.
- Evaluar la integral indefinida\( \int |x|dx \nonumber\) (Pista: Examinar la gráfica de f (x) =|x|.)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.1.
El vocabulario
| Término | Definición |
|---|---|
| antiderivado | Un antiderivado es una función que invierte una derivada. La función A es la antiderivada de la función B si la función B es la derivada de la función A. |
| antidiferenciación | El proceso de búsqueda de antiderivados se denomina antidiferenciación, más comúnmente denominado integración. |
| constante de integración | La constante de integración es la constante C en la ecuación f (x) dx=F (x) +C relacionando la función f (x) y la antiderivada F. |
| integrand | Un integrando es el argumento f (x) en la integral indefinida f (x) dx. |
| integración | El proceso de búsqueda de antiderivados a veces se llama antidiferenciación, pero más comúnmente se conoce como integración. |
Recursos adicionales
PLIX: Jugar, Aprender, Interactuar, EXPLORAR - Antiderivado: Reunirlo
Práctica: Antiderivado
Mundo real: Alto de las Montañas Rocosas