1.7: Introducción a los ángulos
- Page ID
- 107610
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comparación y clasificación de ángulos, como los rectos o verticales, y su relación con líneas y rayos.
Segmento de Línea y Rayo
Un segmento de línea es una porción de una línea con dos puntos finales. Un rayo es una porción de una línea con un punto final. Los segmentos de línea se nombran por sus puntos finales y los rayos se nombran por su punto final y otro punto. En cada caso, se escribe un símbolo de segmento o rayo encima de los puntos. Abajo, el segmento de línea es\(\overline{AB}\) y el rayo es\(\overrightarrow{AB}\).
Ángulos
- Cuando dos rayos se encuentran en sus puntos finales, forman un ángulo.
- Dependiendo de la situación, un ángulo puede ser nombrado con un símbolo de ángulo\(\angle\) y su vértice, o por tres letras.
Si se usan tres letras, la letra media debe ser el vértice. El ángulo de abajo podría llamarse\(\angle B\) o\(\angle ABC\) o\(\angle CBA\). Usa tres letras para nombrar un ángulo si usar una letra no dejaría claro de qué ángulo estás hablando.
El tamaño de un ángulo se mide en grados. Por lo tanto, 'la medida del ángulo ABC' se refiere al tamaño, o medida, del ángulo en grados, a menudo escrito\(m \angle ABC\). Puede usar un software de transportador o geometría para medir ángulos. Recuerda que un círculo completo tiene\(360 ^{\circ}\).
Tipos de ángulos
- Un ángulo que\(0 ^{\circ}\) es exactamente se llama ángulo cero.
- Un ángulo que es menor que\(90 ^{\circ}\) se llama ángulo agudo.
- Un ángulo que es exactamente\(90 ^{\circ}\) (un cuarto de círculo) se llama ángulo recto. Se observa un ángulo recto con un pequeño cuadrado en su vértice.
- Un ángulo que es más de 90pero menor que\(180 ^{\circ}\) se llama ángulo obtuso. Un ángulo que es exactamente\(180 ^{\circ}\) (la mitad de un círculo) se llama ángulo recto.
Identificación del tipo de ángulos
Nombra el ángulo de abajo y clasifícalo por su medida.
\(m \angle F\)o\(m \angle DFE\) o\(m \angle EFD\). Es _____ ángulo.
Elemento interactivo
Agrega texto de elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Elemento interactivo
Ángulos complementarios y suplementarios
Dos ángulos son complementarios si la suma de sus medidas es\(90 ^{\circ}\).
Dos ángulos son complementarios si la suma de sus medidas es\(180 ^{\circ}\).
Dos ángulos que juntos forman un ángulo recto siempre serán suplementarios.
Encontrar un ángulo desconocido
\(x\)y\(y\) son ángulos complementarios con medida de\(y= 20^{\circ}\). ¿Cuál es la medida de\(x\)?
La medida de\(x\) es _____.
Ángulos adyacentes y verticales
Cuando dos líneas se cruzan, se forman muchos ángulos, como se muestra a continuación.
En el diagrama anterior,\(\angle AEC\) y\(\angle AED\) son ángulos adyacentes porque están uno al lado del otro y comparten un rayo. También son suplementarios, porque juntos forman un ángulo recto. \(\angle AEC\)y\(\angle DEB\) se llaman ángulos verticales. Los ángulos verticales siempre tendrán la misma medida.
Considere este problema de ejemplo:
Vamos\(m \angle AEC=x^{\circ}\). \(m \angle DEB\)Demostrar que también debe ser igual\(x^{\circ}\).
Esto demuestra que los ángulos verticales siempre tendrán la misma medida.
Identificar ángulos
Explica por qué debes usar tres letras para identificar cualquiera de los ángulos en el diagrama a continuación.
Todos los ángulos en este diagrama tienen un vértice de E. Por lo tanto, E es ambiguo porque podría referirse a muchos ángulos diferentes. Usa tres letras con E como letra media para tener claro a qué ángulo te refieres\(\angle AEC\),\(\angle AED\),\(\angle DEB\),\(\angle BEC\).
Ejemplo\(\PageIndex{1}\)
Los ángulos están formados por líneas o rayos que se cruzan. Si tomas dos líneas o rayos, ¿formarás al menos un ángulo?
Solución
Siempre y cuando las líneas o rayos se crucen, se formará al menos un ángulo. Si las líneas (o rayos) son paralelas, y por lo tanto no se cruzan, entonces no se formarán ángulos.
Ejemplo\(\PageIndex{2}\)
Estimar la medida del ángulo\(\angle DFE\). Usa un tractor para confirmar tu respuesta.
Solución
Recuerda que exactamente la mitad de un ángulo recto es\(45^{\circ}\). Este ángulo parece ser más de la mitad de un ángulo recto. Podrías adivinar que es aproximadamente\(55^{\circ}\). Usando un trasportador, se puede ver que se trata de\(60^{\circ}\).
Ejemplo\(\PageIndex{3}\)
¿Cómo se llaman dos líneas que forman un ángulo recto?
Solución
Líneas perpendiculares.
Elemento interactivo
Revisar
1. ¿Cuál es la diferencia entre un segmento de línea, una línea y un rayo?
2. Dibuja un ejemplo de ángulo recto.
3. Dibuja un ejemplo de un ángulo obtuso.
4. Dibuja un ejemplo de un ángulo agudo.
5. ¿Por qué dos ángulos que hacen que un ángulo recto sean siempre complementarios?
6. Si\(m\angle ABC= (2x+4)^{\circ}\),\(m\angle DEF= (3x−5)^{\circ}\),\(\angle ABC\) y\(\angle DEF\) son complementarios, ¿cuáles son las medidas de los ángulos?
7. Si\(m\angle ABC= (2x+4)^{\circ}\),\(m\angle DEF= (3x−5)^{\circ}\),\(\angle ABC\) y\(\angle DEF\) son complementarios, ¿cuáles son las medidas de los ángulos?
Utilice el diagrama a continuación para #8 - #12.
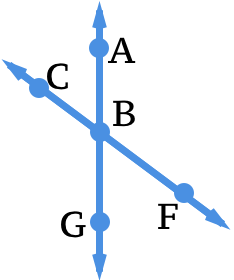Figura\(\PageIndex{12}\)8. Dar un ejemplo de ángulos verticales.
9. Dé un ejemplo de ángulo recto.
10. Dar un ejemplo de ángulos suplementarios.
11. Si\(m\angle ABC= 70^{\circ}\), encuentra\(m\angle ABF\).
12. Si\(m\angle ABC= 70^{\circ}\), encuentra\(m\angle FBG\).
13. ¿Qué recuerdas de las líneas perpendiculares?
Usa el ángulo de la imagen para #14 - #15.
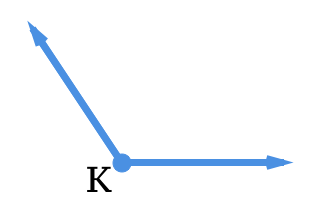Figura\(\PageIndex{13}\)14. Nombra el ángulo y clasifícalo en función de su tamaño.
15. Estimar la medida del ángulo. Usa un tractor para confirmar tu respuesta.
16. Dibuja un diagrama en el que dos ángulos sean complementarios al mismo ángulo. ¿Qué debe ser cierto sobre los dos ángulos originales? Explique.
17. Utilizamos el término complementario para describir ángulos que suman ___ y suplementarios para describir ángulos que suman a ___. ¿Qué pasa con los ángulos que suman\(360^{\circ}\)? Inventa un nombre para tales ángulos y justifica tu elección.
18. Dibuja dos ángulos verticales. ¿Cuánto debe girarse cada rayo de uno de los ángulos verticales para que coincida con el otro ángulo vertical? Explique.
19. Dibuja dos ángulos de la misma medida que no sean verticales. Dibuja dos ángulos que sean suplementarios pero no adyacentes. Dibuja dos ángulos que sean adyacentes y tengan la misma medida. ¿Cuál es la medida de cada ángulo en el último dibujo? ¿Por qué?
Reseña (Respuestas)
Para ver las respuestas de la opinión, haga clic aquí.
Recursos adicionales
Elemento interactivo
Video: Comparando ángulos
Práctica: Introducción a los ángulos