2.1: Patrones visuales básicos
- Page ID
- 107374
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Describir secuencias no aritméticas mediante la búsqueda de una regla. Identificar patrones visuales y geométricos
Figura\(\PageIndex{1}\)Whitney está de viaje escolar a Italia. El quinto día allí su grupo visita Venecia donde llega a ver el Palacio Ducal. Ella nota un patrón visual en la arquitectura y tomó la foto de arriba. ¿Cómo podría Whitney describir este patrón visual? ¿Qué tipo de patrón visual es?
En este concepto, aprenderás a reconocer, describir y extender patrones visuales.
Patrones visuales
Un patrón visual es una secuencia de imágenes u objetos geométricos que se han creado con base en alguna regla. Hay dos categorías de patrones visuales que conocerás aquí.
- Algunos patrones visuales están formados por una secuencia de imágenes u objetos geométricos que se repiten una y otra vez. Estos tipos de patrones se denominan patrones repetitivos. La secuencia de imágenes que se repiten se llama unidad de patrón.
- Algunos patrones visuales se basan en una imagen u objeto geométrico que sigue aumentando o disminuyendo de tamaño de una manera específica. Este tipo de patrones tienen una regla de patrón que ayuda a describir cómo la imagen u objeto está creciendo o encogiendo.
Aquí hay un ejemplo de un patrón visual que es un patrón repetitivo.
Encuentre la unidad de patrón para el patrón a continuación.
Figura\(\PageIndex{2}\)Primero, observe que este patrón visual está formado por círculos, cuadrados y triángulos.
A continuación, mire con atención para ver cómo se han colocado las formas. Después de cada círculo es un cuadrado, después de cada cuadrado hay dos triángulos, y después de cada par de triángulos hay otro círculo. Este es un patrón repetitivo porque el mismo conjunto de cuatro imágenes se repite una y otra vez.
La unidad de patrón para este patrón visual es el conjunto de imágenes que se repite.
La respuesta es que la unidad de patrón es “círculo, cuadrado, triángulo, triángulo”:
Figura\(\PageIndex{3}\)Una vez que entiendas el patrón y conozcas la unidad de patrón, puedes extender el patrón. El siguiente cuadro de nuestra secuencia de imágenes sería un triángulo.
Aquí hay un ejemplo de un patrón visual creciente.
Encuentre una regla de patrón para describir el patrón a continuación. ¿Cómo será el siguiente paso en el patrón?
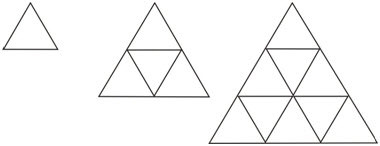Figura\(\PageIndex{4}\)Como puedes ver, este patrón es diferente de un patrón repetitivo porque los objetos geométricos siguen haciéndose cada vez más grandes. No hay una unidad de patrón que se repita, pero se puede encontrar una regla de patrón para describir lo que está sucediendo.
Para encontrar la regla del patrón, busque ver cómo se relacionan los pasos en el patrón. Cada nuevo triángulo grande está formado por cada vez más triángulos más pequeños. De hecho, cada nuevo triángulo grande está conformado por el triángulo grande anterior más una fila adicional de triángulos pequeños.
- El primer paso en el patrón tiene solo una fila de 1 triángulo.
- El segundo paso en el patrón tiene dos filas de 1 triángulo, luego 3 triángulos.
- El tercer paso en el patrón tiene tres filas de 1 triángulo, luego 3 triángulos, luego 5 triángulos.
Se puede ver que el número de filas de triángulos corresponde al paso en el patrón. Cada vez que se agrega una nueva fila, tiene 2 triángulos más que la fila por encima de ella.
La respuesta para la regla del patrón es: para obtener el siguiente paso en el patrón, dar el paso anterior y agregar otra fila de triángulos pequeños al fondo con 2 triángulos más que la fila por encima de él.
Ahora que tienes la regla del patrón, puedes extender el patrón.
Se esperaría que el siguiente paso en el patrón se vea como el tercer paso en el patrón excepto con una fila adicional de triángulos.
La respuesta es que el cuarto paso en el patrón tendrá cuatro filas de 1 triángulo, luego 3 triángulos, luego 5 triángulos, luego 7 triángulos:
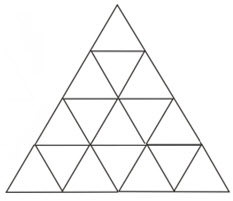Figura\(\PageIndex{5}\)Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Whitney y su viaje escolar a Italia.
Llegó a ver el Palacio Ducal en Venecia donde notó un interesante patrón visual en la arquitectura.
Solución
Primero, fíjese que se trata de un patrón repetitivo. Los objetos se están repitiendo en lugar de aumentar/disminuir de tamaño.
Como este es un patrón repetitivo, a continuación intente describir la unidad de patrón.
La misma columna con barandilla se repite una y otra vez. Esta es la unidad de patrón.
La respuesta es que este es un patrón repetitivo con una unidad de patrón que es un par columna/barandilla.
Ejemplo\(\PageIndex{2}\)
¿Cómo será el siguiente paso en el patrón a continuación?
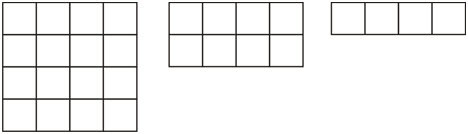Figura\(\PageIndex{6}\)Solución
Primero, observe que este es un patrón visual decreciente.
Para encontrar la regla del patrón, busque ver cómo se relacionan los pasos en el patrón. Cada nuevo rectángulo está compuesto por cada vez menos cuadrados. De hecho, cada nuevo rectángulo está formado por la mitad de cuadrados que el rectángulo anterior.
- El primer paso en el patrón tiene 16 cuadrados.
- El segundo paso en el patrón tiene 8 cuadrados.
- El tercer paso en el patrón tiene 4 cuadrados.
Puedes ver que si tomas el número de cuadrados en un paso del patrón y lo divides por 2, obtendrás el número de cuadrados en el siguiente paso del patrón.
La respuesta es que la regla del patrón es obtener el número de cuadrados en el siguiente paso en el patrón, tomar el número de cuadrados en el paso anterior y dividir por 2.
Ahora que tienes la regla del patrón, puedes extender el patrón.
Se esperaría que el siguiente paso en el patrón tuviera la mitad de cuadrados que el tercer paso. El tercer escalón tiene 4 cuadrados, por lo que el cuarto escalón tendrá dos cuadrados.
La respuesta es que el siguiente paso en el patrón se verá así:
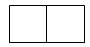Figura\(\PageIndex{7}\)Ejemplo\(\PageIndex{3}\)
Describa el siguiente patrón. ¿Cuál es su unidad de patrón o regla de patrón?
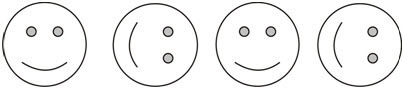Figura\(\PageIndex{8}\)Solución
Primero note que se trata de un patrón repetitivo. Las imágenes se están repitiendo en lugar de aumentar/disminuir de tamaño.
A continuación, mire con atención para ver cómo se han colocado las imágenes. Después de cada carita sonriente con la boca en la parte inferior hay una cara sonriente con la boca a la izquierda. El mismo conjunto de dos imágenes se repite una y otra vez.
La respuesta es que se trata de un patrón repetitivo. La unidad de patrón es:
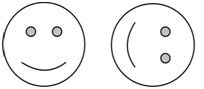Figura\(\PageIndex{9}\)Ejemplo\(\PageIndex{4}\)
Describa el siguiente patrón. ¿Cuál es su unidad de patrón o regla de patrón?
Figura\(\PageIndex{10}\)Solución
Primero note que se trata de un patrón repetitivo. Las imágenes se están repitiendo en lugar de aumentar/disminuir de tamaño.
A continuación, mire con atención para ver cómo se han colocado las imágenes. Después de cada conjunto de líneas es una flecha. El mismo conjunto de dos imágenes se repite una y otra vez.
La respuesta es que se trata de un patrón repetitivo. La unidad de patrón es:
Figura\(\PageIndex{11}\)Ejemplo\(\PageIndex{5}\)
Continuar con el patrón descrito con las siguientes dos formas.
Triángulo, estrella, triángulo, estrella, cuadrado, cuadrado, triángulo, estrella, triángulo
Solución
Primero note que se trata de un patrón repetitivo. Las imágenes no se han visualizado, pero se han descrito. Las imágenes se están repitiendo en lugar de aumentar/disminuir de tamaño.
A continuación, mire con atención para ver cómo se han ordenado las formas. Después de “triángulo, estrella, triángulo, estrella” es “cuadrado, cuadrado”. Después de “cuadrado, cuadrado” parece repetirse la secuencia de “triángulo, estrella,...”. Parece que el mismo conjunto de seis formas se repetirá una y otra vez.
La unidad de patrón es “triángulo, estrella, triángulo, estrella, cuadrado, cuadrado”.
Ahora que tienes la unidad de patrón, puedes extender el patrón. Después del “triángulo, estrella, triángulo” al final del patrón habrá otra estrella, luego dos cuadrados, y luego de vuelta al inicio de la unidad de patrón con “triángulo, estrella, triángulo, estrella, cuadrado, cuadrado...”.
La respuesta es que las siguientes dos formas serán “estrella, cuadrada”.
Revisar
Escribe una regla para cada patrón numérico.
- \(4,7,13,25\)
- \(216,196,176,156\)
- \(1,7,19,43\)
- \(10,000, 1,000, 100, 10\)
Escribe el siguiente número en cada patrón.
- \(4,7,13,25,_____\)
- \(216,196,176,156, _____\)
- \(1, 7, 19, 43,_____\)
- \(10,000, 1,000, 100, 10, _____\)
Anota la siguiente imagen en cada patrón basado en la descripción.
- Un hexágono, un pentágono, un cuadrado, _____
- Cinco puntos, diez puntos, quince puntos, _____
- Quince puntos, catorce puntos, doce puntos, _____
- Dos triángulos, cuatro triángulos, tres triángulos, seis triángulos, cinco triángulos, _____
- Un octágono, un hexágono, un octágono, un pentágono, un octágono, ____
- Un cuadrado, 1.5 cuadrados, 2 cuadrados, 2.5 cuadrados, _____
- Dieciocho círculos, nueve círculos, cuatro círculos y medio _____
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.3.
Recursos adicionales
Elemento Interactivo
Video: Secuencias geométricas (Introducción)
Práctica: Patrones visuales básicos
Mundo real: Las matemáticas detrás de todo