Saltar al contenido principal
LibreTexts Español

2.16: Pruebas de paralelogramo

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    107341

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Aplicar teoremas para mostrar si un cuadrilátero tiene dos pares de lados paralelos.

    Cuadriláteros que son Paralelogramos

    Recordemos que un paralelogramo es un cuadrilátero con dos pares de lados paralelos. Aunque un cuadrilátero no esté marcado con tener dos pares de lados, aún podría ser un paralelogramo. La siguiente es una lista de teoremas que te ayudarán a decidir si un cuadrilátero es un paralelogramo o no.

    1. Teorema de lados opuestos Converse: Si ambos pares de lados opuestos de un cuadrilátero son congruentes, entonces la figura es un paralelogramo.

    Si

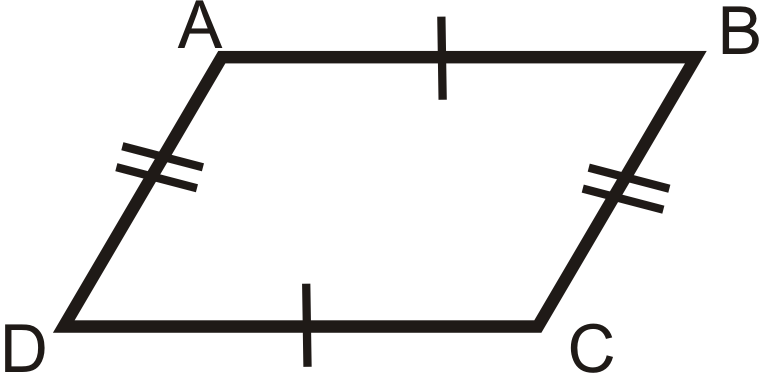
    f-d_b44f3f753ae5d2c0f64fe05ea27747fece73e8409e7a42a40ebe4a1b+image_tiny+image_tiny.png
    Figura\(\PageIndex{1}\)

    entonces

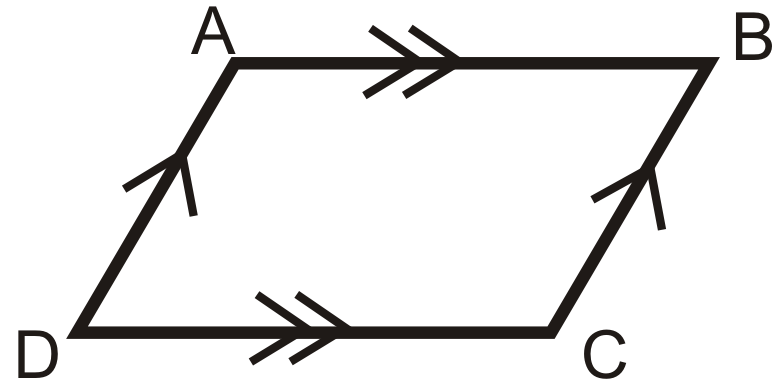
    f-d_994d6497cbae0e45c57daa4d03e6067e99015df4ccb97c8bf5a14596+image_tiny+image_tiny.png
    Figura\(\PageIndex{2}\)

    2. Teorema de ángulos opuestos Converse: Si ambos pares de ángulos opuestos de un cuadrilátero son congruentes, entonces la figura es un paralelogramo.

    Si

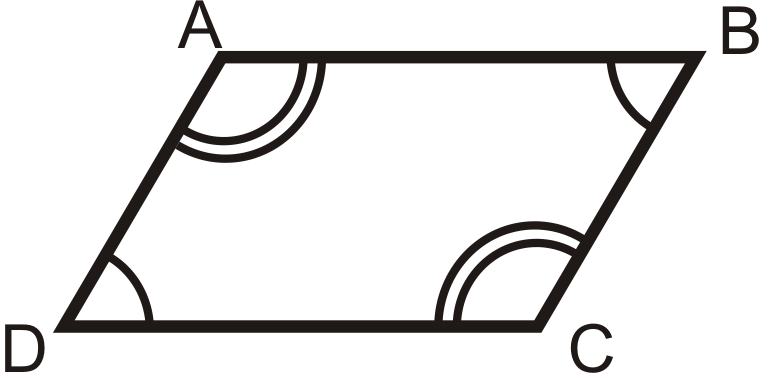
    F-D_2118168440f8fc1a13c1238ef26d6fa54c1173fb4e7e4e2a20c7199c+imagen_tiny+imagen_tiny.png
    Figura\(\PageIndex{3}\)

    entonces

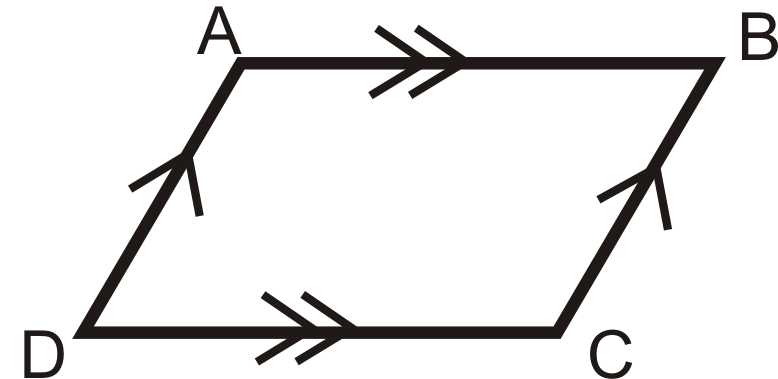
    F-D_528830801800A01007E868C589B2EBF40AB26919F4557BE5E605481A+Image_Tiny+Image_Tiny.png
    Figura\(\PageIndex{4}\)

    3. Paralelogramo Diagonales Teorema Converse: Si las diagonales de un cuadrilátero se bisecan entre sí, entonces la figura es un paralelogramo.

    Si

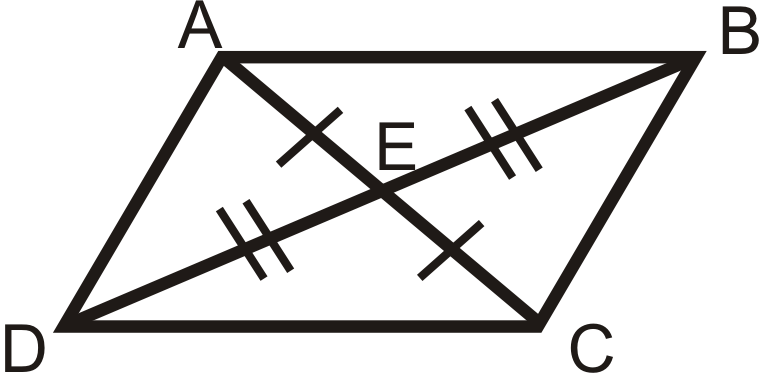
    f-d_46c004c44a75296d2eac72bd737291bae01ab65e1820b5204f3586ca+image_tiny+image_tiny.png
    Figura\(\PageIndex{5}\)

    entonces

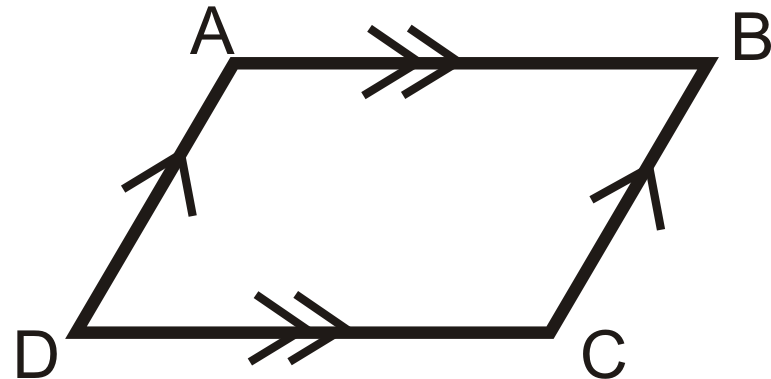
    f-d_c6443e1c10cf2e9c4d75ba5b555b815d0a95690ca23ea976a0b40e5f+image_tiny+image_tiny.png
    Figura\(\PageIndex{6}\)

    4. Teorema de Lados Congruentes Paralelos: Si un cuadrilátero tiene un conjunto de líneas paralelas que también son congruentes, entonces es un paralelogramo.

    Si

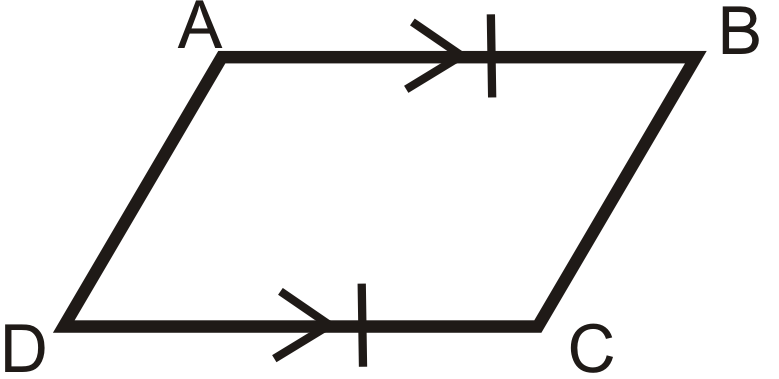
    F-D_E46203F33A4881541307B95407D5031345EDCB82AE45185EA0C3AA76+Image_Tiny+Image_Tiny.png
    Figura\(\PageIndex{7}\)

    entonces

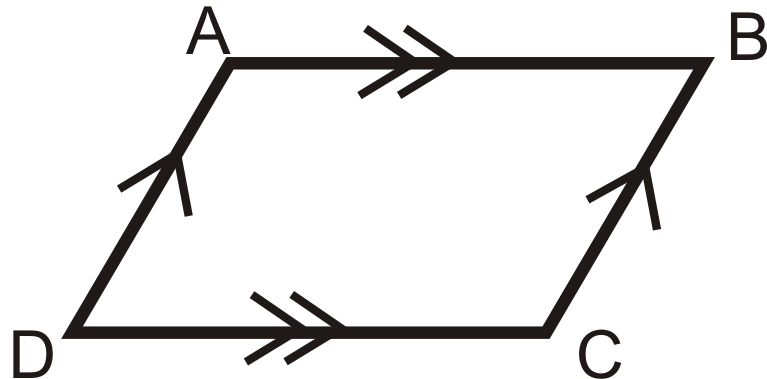
    f-d_7d8fcf2fea2284750352c44fdde20db6255d6298f2cf47be907ff997+image_tiny+image_tiny.png
    Figura\(\PageIndex{8}\)

    Puedes usar cualquiera de los teoremas anteriores para ayudar a mostrar que un cuadrilátero es un paralelogramo. Si estás trabajando en el plano x−y, es posible que necesites conocer las fórmulas que se muestran a continuación para ayudarte a usar los teoremas.

    • La Fórmula de la Pendiente,\(\dfrac{y_2−y_1}{x_2−x_1}\). (Recuerda que si las pendientes son las mismas entonces las líneas son paralelas).
    • La Fórmula de Distancia,\(\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). (Esto te ayudará a demostrar que dos lados son congruentes).
    • La fórmula del punto medio,\( ( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} )\). (Si los puntos medios de las diagonales son los mismos entonces las diagonales se bisecan entre sí).

    ¿Y si te dieran cuatro pares de coordenadas que forman un cuadrilátero? ¿Cómo podrías determinar si ese cuadrilátero es un paralelogramo?

    Ejemplo\(\PageIndex{1}\)

    Demostrar el teorema de los lados congruentes paralelos.

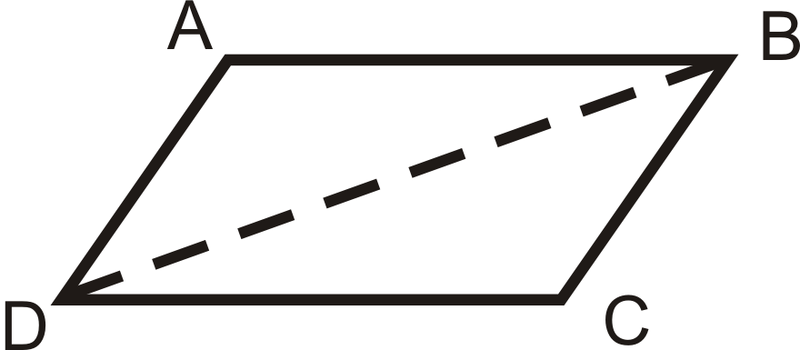
    F-D_481247021bd2921618edf2f5e05543ff7668412a6a797825b7b69f29+image_tiny+image_tiny+image_tiny.png
    Figura\(\PageIndex{9}\)

    Dado:\(\overline{AB}\parallel\overline{DC}\), y\(\overline{AB}\cong \overline{DC}\)

    Probar:\(ABCD\) es un paralelogramo

    Solución

    Comunicado Razón
    1. \(\overline{AB}\parallel\overline{DC}\), y\(\overline{AB}\cong \overline{DC}\) 1. Dado
    2. \(\angle ABD\cong \angle BDC\) 2. Ángulos interiores alternos
    3. \(\overline{DB}\cong \overline{DB}\) 3. reflexivo\(PoC\)
    4. \(\Delta ABD\cong \Delta CDB\) 4. SAS
    5. \(\overline{AD}\cong \overline{BC}\)\) 5. CPCTC
    6. \(ABCD\)es un paralelogramo 6. Lados opuestos Converse

    Ejemplo\(\PageIndex{2}\)

    ¿Qué valor de\(x\) haría\(ABCD\) un paralelogramo?

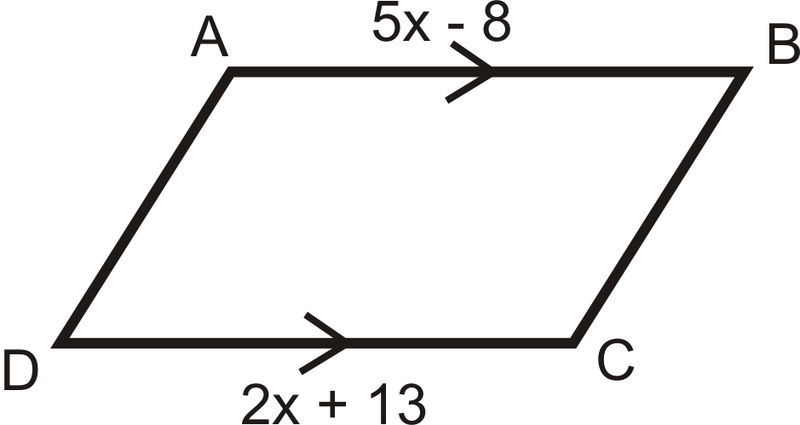
    F-D_57BE9D320081B376883EC8CAD8136DEDF5E1644F34D20438C1632327+Image_Tiny+Image_Tiny.png
    Figura\(\PageIndex{10}\)

    Solución

    \(\overline{AB}\parallel\overline{DC}\). Por el Teorema de Lados Congruentes\(ABCD\) Paralelos, sería un paralelogramo si\(AB=DC\).

    \(\begin{align*} 5x−8 &=2x+13 \\ 3x &=21 \\ x &=7 \end{align*}\)

    Ejemplo\(\PageIndex{3}\)

    Demostrar los lados opuestos Teorema Converse.

    F-D_481247021bd2921618edf2f5e05543ff7668412a6a797825b7b69f29+image_tiny+image_tiny+image_tiny.png
    Figura\(\PageIndex{11}\)

    Teniendo en cuenta:\(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC}\)

    Probar:\(ABCD\) es un paralelogramo

    Solución

    Comunicado Razón
    1. \(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC}\) 1.Dado
    2. \(\overline{DB}\cong \overline{DB}\) 2. reflexivo\(PoC\)
    3. \(\Delta ABD\cong \Delta CDB\) 3. SSS
    4. \(\angle ABD\cong \angle BDC\),\(\angle ADB\cong \angle DBC\) 4. \(CPCTC\)
    5. \(\overline{AB}\parallel\overline{DC}\),\(\overline{AD}\parallel\overline{BC}\) 5. Converse de ángulos interiores alternos
    6. \(ABCD\)es un paralelogramo 6. Definición de un paralelogramo

    Ejemplo\(\PageIndex{4}\)

    ¿El cuadrilátero es\(EFGH\) un paralelogramo? ¿Cómo lo sabes?

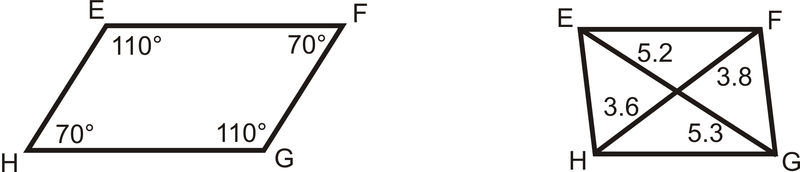
    f-d_b1740b63357c5d41fd536f61ac4336ce081028133139b46445b5a7af+image_tiny+image_tiny.png
    Figura\(\PageIndex{12}\)

    Solución

    Por el Teorema de Ángulos Opuestos Converse,\(EFGH\) es un paralelogramo.

    \(EFGH\)no es un paralelogramo porque las diagonales no se bisecan entre sí.

    Ejemplo\(\PageIndex{5}\)

    ¿El cuadrilátero es\(ABCD\) un paralelogramo?

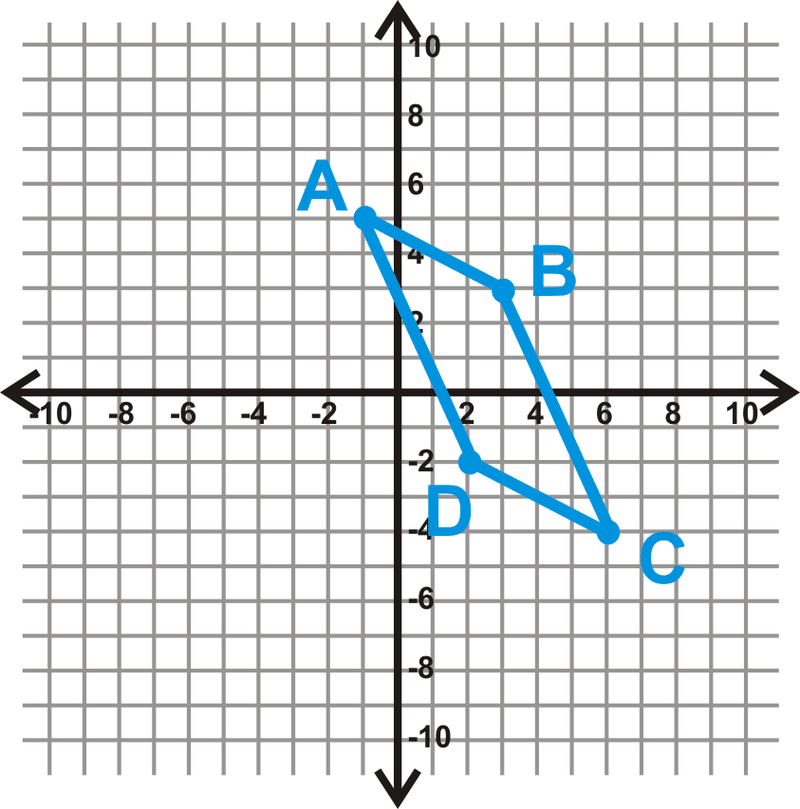
    f-d_ad6c14bc1b86d3eeeaa76acbda23277a9070ebd2c788dea374e53bbc+image_tiny+image_tiny.png
    Figura\(\PageIndex{13}\)

    Solución

    Usemos el Teorema de Lados Congruentes Paralelos para ver si\(ABCD\) es un paralelogramo. Primero, encuentra la longitud de AB y CD usando la fórmula de distancia.

    \(\begin{align*} AB &=\sqrt{(−1−3)^2+(5−3)^2} & CD &=\sqrt{(2−6)^2+(−2+4)^2} \\ &=\sqrt{(−4)^{2}+2^2} & &=\sqrt{(−4)^2+2^2} \\ &=\sqrt{16+4}=\sqrt{20} & & =\sqrt{16+4}=\sqrt{20} \end{align*}\)

    A continuación encuentra las pendientes para comprobar si las líneas son paralelas.

    \(\begin{align*} Slope \: AB =\dfrac{5−3}{−1−3} =\dfrac{2}{−4} &=−\dfrac{1}{2} &Slope \: CD=\dfrac{−2+4}{2−6}=\dfrac{2}{−4}=−\dfrac{1}{2} \end{align*}\)

    \(AB=CD\)y las pendientes son las mismas (lo que implica que las líneas son paralelas), así\(ABCD\) es un paralelogramo.

    Revisar

    Para las preguntas 1-12, determine si los cuadriláteros son paralelogramos.


    1. f-d_f115e63a62ea93db5c7c2626104f16d483f975e8fb7d2ce76dce2651+image_tiny+imagen_tiny.png
      Figura\(\PageIndex{14}\)
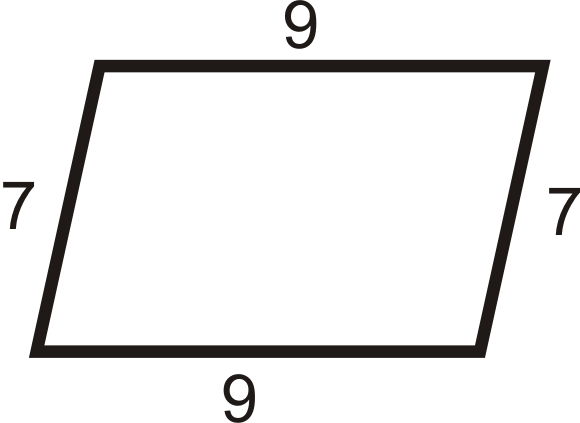
    2. f-d_d4552bb5eb475c4c4ce3f5b1bbcbc5a5a529242c4e35b20e4d16b53475+image_tiny+image_tiny.png
      Figura\(\PageIndex{15}\)
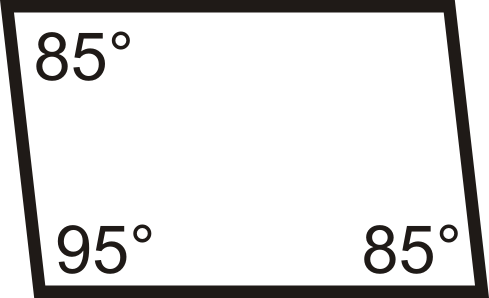
    3. f-d_6e35e37accd9e3dfbd07885a830ad68194d5e01d384acf20f8b48d8e+image_tiny+image_tiny.png
      Figura\(\PageIndex{16}\)
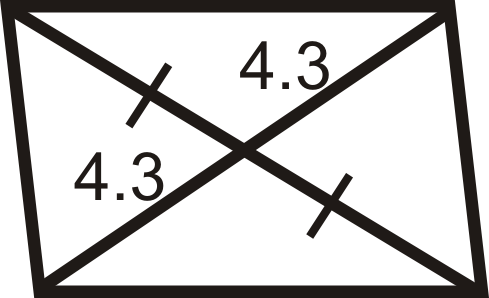
    4. F-D_24cfeae21b610c1ef10b4fb97b5212b20d60593b74aa485a85d1a5cd+image_tiny+image_tiny.png
      Figura\(\PageIndex{17}\)
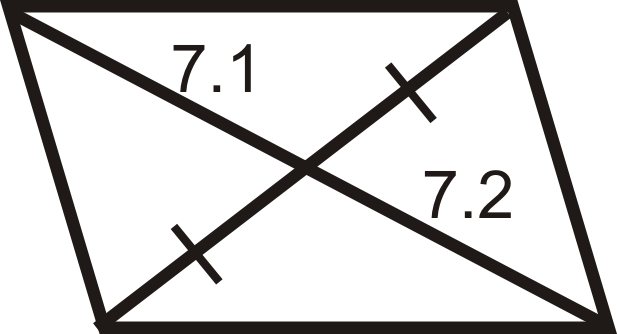
    5. f-d_44353c64a9f78624e106f20154cd9f99181debe964e91b4047f2973c+image_tiny+image_tiny.png
      Figura\(\PageIndex{18}\)
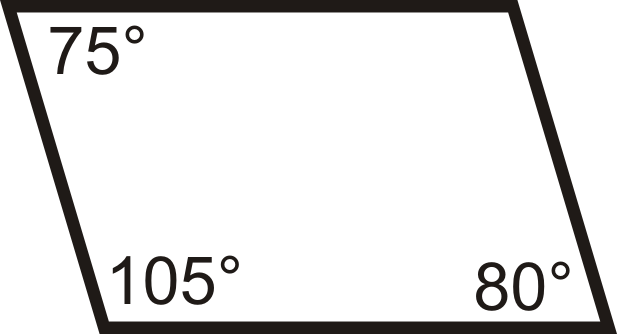
    6. F-d_a872533899b5e49c28e959cd6bdcf8536a59b66b67d863c5d332452d+image_tiny+imagen_tiny.png
      Figura\(\PageIndex{19}\)
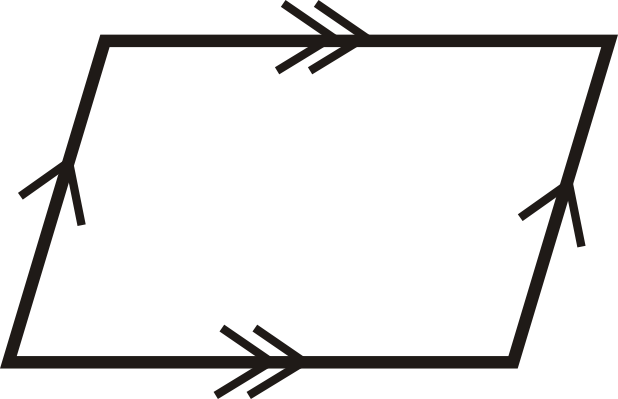
    7. f-d_f099d07dd39fc5387cb4b57ef6718c22cca19fc3bada97ce191a6d3c+image_tiny+imagen_tiny.png
      Figura\(\PageIndex{20}\)
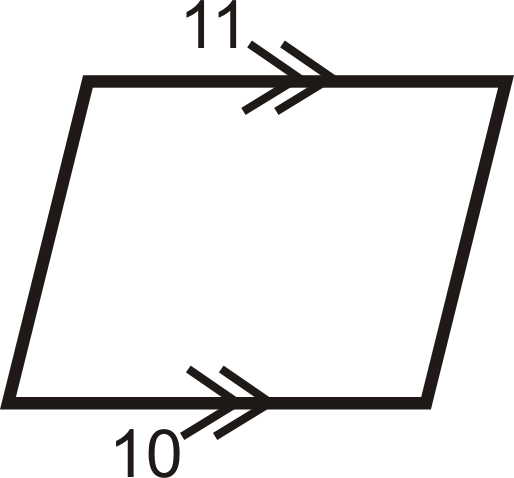
    8. f-d_693a8ec5c82d2b046ae574582eb1e6f1d7f4a999dfab808061a26406+image_tiny+image_tiny.png
      Figura\(\PageIndex{21}\)
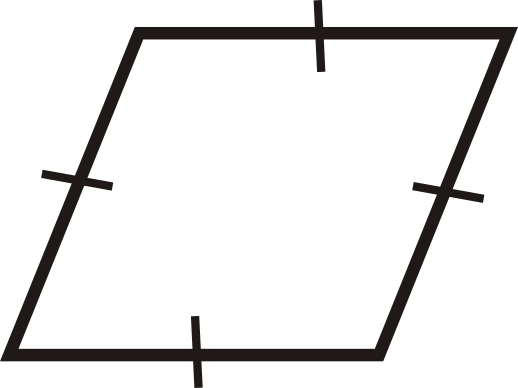
    9. f-d_aa10e238732f18cd00acc1324d6bc0b283aa6be2ee92559b3fb1718d+image_tiny+image_tiny.png
      Figura\(\PageIndex{22}\)
    10. f-d_1e7c0639f04b1522952e96b432d4ef96930fc55563a7f0762c96643f+image_tiny+image_tiny.png
      Figura\(\PageIndex{23}\)
    11. f-d_098fceba94a4685311ba9bbd93bde184c39b57bef6c4f493e4b25f03+image_tiny+image_tiny.png
      Figura\(\PageIndex{24}\)
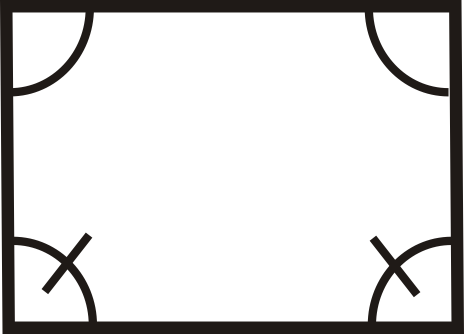
    12. f-d_3c7e18be2f36809db07c1f98cd412b8c452bc11585c76408ea1ed6be+image_tiny+image_tiny.png
      Figura\(\PageIndex{25}\)

    Para las preguntas 13-18, determinar el valor de\(x\) y\(y\) eso haría del cuadrilátero un paralelogramo.


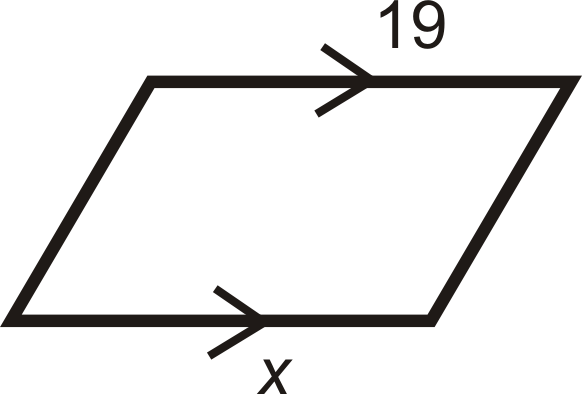
    1. f-d_1539ca43a25a0987c6ec6a5c3bf136b42087fe789e8b551ba121479e+image_tiny+image_tiny.png
      Figura\(\PageIndex{26}\)
    2. f-d_f779028e7d8b015f18326b4aa28e0043d1270e0aaaa7253c6282e096+image_tiny+image_tiny.png
      Figura\(\PageIndex{27}\)
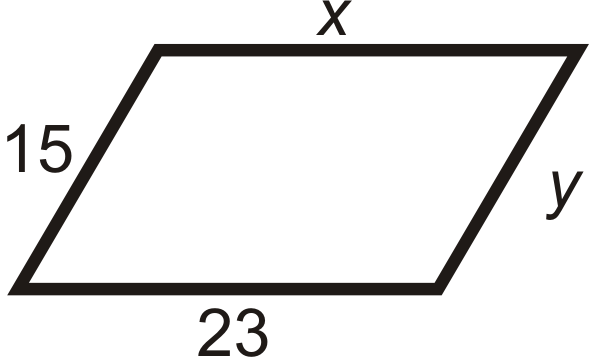
    3. F-d_82c1c140c26b3569c7f61c021a892308a80816efd2c32dc79a777ed5+image_tiny+image_tiny.png
      Figura\(\PageIndex{28}\)
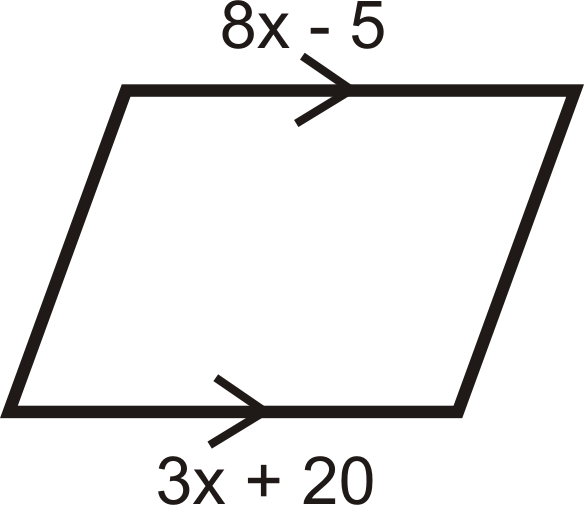
    4. f-d_cbd0d4db01f59e53f702d0678534bf3c369bd54ac751831222fd6e13+image_tiny+image_tiny.png
      Figura\(\PageIndex{29}\)
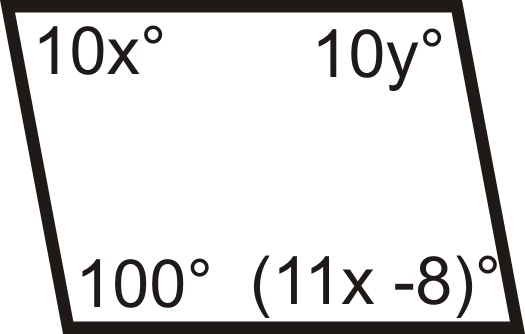
    5. f-d_ef3d72d5ae275cfd7f794254471af20f5978e7818d4571316bd86f79+image_tiny+image_tiny.png
      Figura\(\PageIndex{30}\)
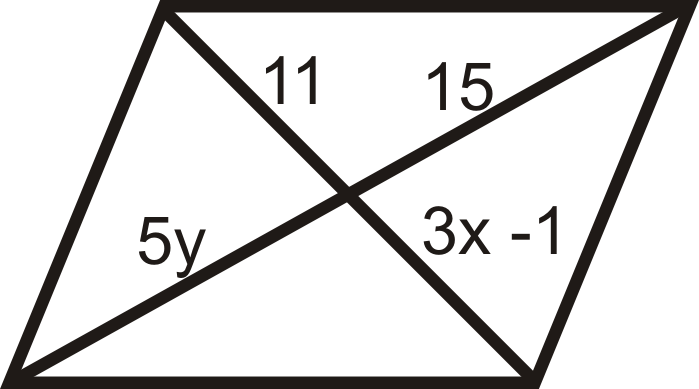
    6. f-d_9e4b4d0af7226ede7751c9928b9412b04996fb55808ad75983dd3319+image_tiny+image_tiny+image_tiny.png
      Figura\(\PageIndex{31}\)

    Para las preguntas 19-22, determine si\(ABCD\) es un paralelogramo.

    1. \(A(8,−1)\),\(B(6,5)\),\(C(−7,2)\),\(D(−5,−4)\)
    2. \(A(−5,8)\),\(B(−2,9)\),\(C(3,4)\),\(D(0,3)\)
    3. \(A(−2,6)\),\(B(4,−4)\),\(C(13,−7)\),\(D(4,−10)\)
    4. \(A(−9,−1)\),\(B(−7,5)\),\(C(3,8)\),\(D(1,2)\)

    Rellene los espacios en blanco en las pruebas a continuación.

    1. Teorema de ángulos opuestos Converse
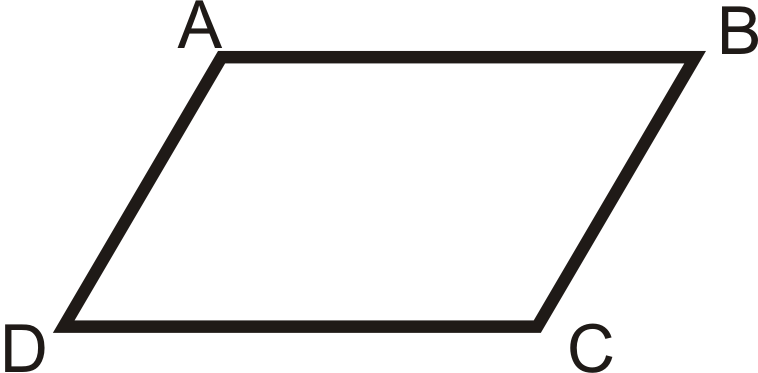
    F-D_14c5c7af431574174f61e564b4ce1c17a9f6dafef030e565b85454c6+imagen_tiny+image_tiny.png
    Figura\(\PageIndex{32}\)

    Teniendo en cuenta:\(\angle A\cong \angle C\),\(\angle D\cong \angle B\)

    Probar:\(ABCD\) es un paralelogramo

    Comunicado Razón
    1. 1.
    2. \(m\angle A=m\angle C\),\(m\angle D=m\angle B\) 2.
    3. 3. Definición de cuadrilátero
    4. \(m\angle A+m\angle A+m\angle B+m\angle B=360^{\circ}\) 4.
    5. 5. Combinar términos similares
    6. 6. División\(PoE\)
    7. \(\angle A\)y\(\angle B\) son complementarios\(\angle A\) y\(\angle D\) complementarios 7.
    8. 8. Converse Converse Converse
    9. \(ABCD\)es un paralelogramo 9.
    1. Paralelogramo Diagonales Teorema Converse
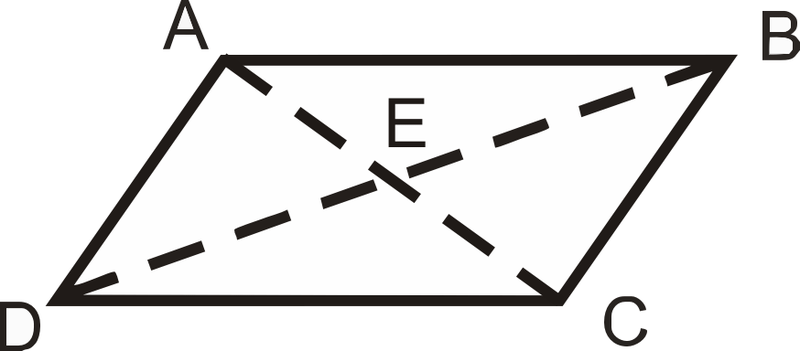
    F-D_4c50cdd807989540195ffb2226df7dc09513ff33267308d9f8203ca8+image_tiny+image_tiny.png
    Figura\(\PageIndex{33}\)

    Teniendo en cuenta:\(\overline{AE}\cong \overline{EC}\),\(\overline{DE}\cong \overline{EB}\)

    Probar:\(ABCD\) es un paralelogramo

    Comunicado Razón
    1. 1.
    2. 2. Teorema de ángulos verticales

    3. \(\Delta AED \cong \Delta CEB\)

    \(\Delta AEB\cong \Delta CED\)

    		 3.
    4. 4.
    5. \(ABCD\)es un paralelogramo 5.
    1. Teniendo en cuenta:\(\angle ADB\cong \angle CBD\),\(\overline{AD}\cong \overline{BC}\)

    Probar:\(ABCD\) es un paralelogramo

    F-D_481247021bd2921618edf2f5e05543ff7668412a6a797825b7b69f29+image_tiny+image_tiny+image_tiny.png
    Figura\(\PageIndex{34}\)
    Comunicado Razón
    1. 1.
    2. \(\overline{AD}\parallel\overline{BC}\) 2.
    3. \(ABCD\)es un paralelogramo 3.

    Reseña (Respuestas)

    Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.4.

    Recursos adicionales

    Elemento Interactivo

    Video: Demostrar un cuadrilátero es un paralelogramo Principios - Básico

    Actividades: Cuadriláteros que son Paralelogramas Preguntas de Discusión

    Ayudas de estudio: Guía de estudio de paralelogramos

    Práctica: Pruebas de paralelogramo

    Mundo real: cuadriláteros que son paralelogramos

    This page titled 2.16: Pruebas de paralelogramo is shared under a CK-12 license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform.

    CK-12 Foundation
    LICENSED UNDER
    CK-12 Foundation is licensed under CK-12 Curriculum Materials License