2.13: Introducción a las Pruebas

Última actualización
Guardar como PDF

Page ID: 107358

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Utilizar pruebas de dos columnas para afirmar y probar la validez de una declaración escribiendo argumentos formales de declaraciones matemáticas. También aprenda sobre los formatos de prueba de párrafo y diagrama de flujo.

Pruebas de dos columnas

Una prueba de dos columnas es una forma común de organizar una prueba en geometría. Las pruebas de dos columnas siempre tienen dos columnas: una para declaraciones y otra para razones. La mejor manera de entender las pruebas de dos columnas es leer ejemplos.

Al escribir su propia prueba de dos columnas, tenga en cuenta estas cosas:

Numere cada paso.
Comience con la información dada.
Las declaraciones con la misma razón se pueden combinar en un solo paso. Depende de usted.
Dibuja un cuadro y márcalo con la información dada.
Debes tener un motivo para CADA declaración.
El orden de las declaraciones en la prueba no siempre es fijo, sino asegurarse de que el orden tenga sentido lógico.
Las razones serán definiciones, postulados, propiedades y teoremas previamente probados. “Dado” sólo se utiliza como razón si la información en la columna de declaración se dio en el problema.
Utilice símbolos y abreviaturas para las palabras dentro de las pruebas. Por ejemplo, se\(\cong\) puede utilizar en lugar de la palabra congruente. También podrías usar\ (\ ángulo para la palabra ángulo.

Supongamos que te dicen que\(\angle XYZ\) es un ángulo recto y que\(\overrightarrow{YW}\) bisecta\(\angle XYZ\). Entonces se le pide que demuestre\(\angle XYW\cong \angle WYZ\).

Ejemplo\(\PageIndex{1}\)

Escriba una prueba de dos columnas para lo siguiente:

Si\(A\),\(B\),\(C\), y\(D\) son puntos en una línea, en el orden dado, y\(AB=CD\), entonces\(AC=BD\).

Solución

Cuando la declaración se da de esta manera, la parte de “si” es la dada y la parte de “entonces” es lo que estamos tratando de probar.

Siempre empieza por dibujar una imagen de lo que te dan.

Trazar los puntos en el orden\(A\),\(B\),\(C\),\(D\) en una línea.

f-d_c0b0cfe92c9fe28800ba8be560da359ac06ce5f4c4bc9db8a9e3efe2+image_tiny+image_tiny.png — Figura\(\PageIndex{1}\)

Agregar lo dado,\(AB=CD\).

f-d_c2a1806254611af4120698fd8b46a4fda3c2c557336aad9c8f58c0ab+image_tiny+image_tiny.png — Figura\(\PageIndex{2}\)

Dibuja la prueba de dos columnas y comienza con la información dada.

*Declaración*	*Razón*
1. \(A\),\(B\),\(C\), y\(D\) son colineales, en ese orden.	1. Dado
2. \(AB=CD\)	2. Dado
3. \(BC=BC\)	3. PoE reflexivo
4. \(AB+BC=BC+CD\)	4. Adición PoE
5. \(AB+BC=AC\) \(BC+CD=BD\)	5. Postulado de adición de segmentos
6. \(AC=BD\)	6. Sustitución o PoE Transitivo

Ejemplo\(\PageIndex{2}\)

Escriba una prueba de dos columnas.

Dado:\(\overrightarrow{BF}\) bisectos\(\angle ABC\);\(\angle ABD\cong \angle CBE\)

Demostrar:\(\angle DBF\cong \angle EBF\)

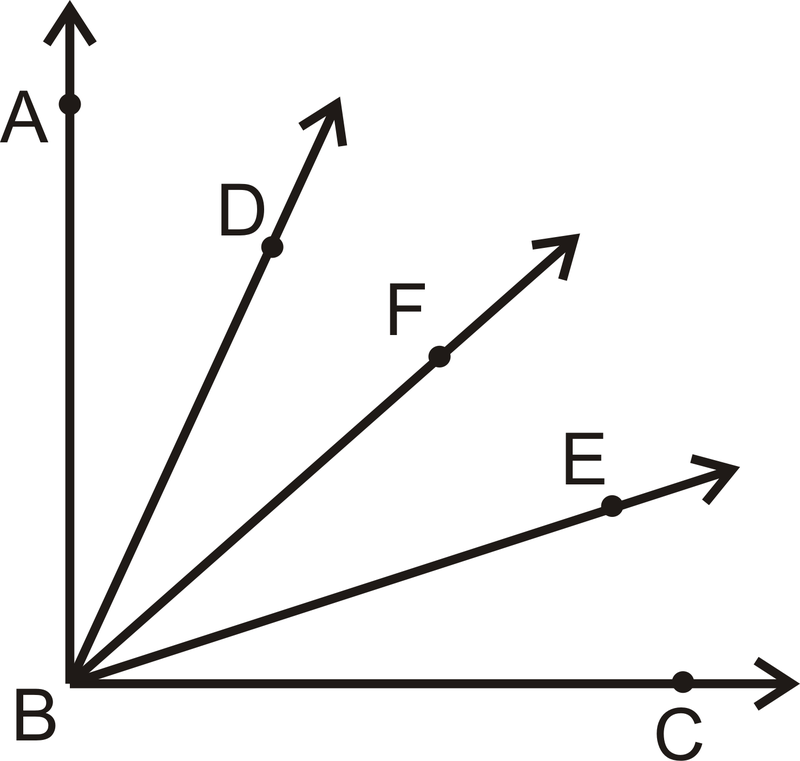f-d_3f8db750b593cdef4e8667fd82405d4b3cbe482a07b311de5b378a30+image_tiny+image_tiny.png

Solución

Primero, ponga las marcas apropiadas en la imagen. Recordemos, ese bisecto significa “cortar por la mitad”. Por lo tanto,\(m\angle ABF=m\angle FBC\).

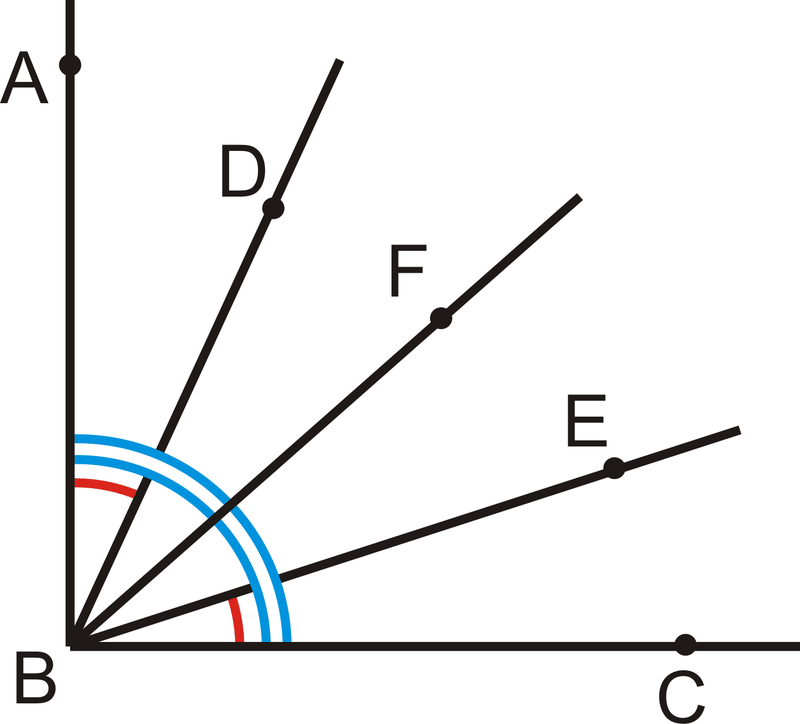
f-d_c53af55d7a322745826d215207c8222716692e1a0b9fcbc10f65b718+image_tiny+imagen_tiny.png — Figura\(\PageIndex{4}\)

*Comunicado*	*Razón*
1. \(\overrightarrow{BF}\)bisectos\(\angle ABC\),\(\angle ABD\cong \angle CBE\)	1. Dado
2. \(m\angle ABF=m\angle FBC\)	2. Definición de una bisectriz angular
3. \(m\angle ABD=m\angle CBE\)	3. Si los ángulos son\(\cong\), entonces sus medidas son iguales.
4. \(m\angle ABF=m\angle ABD+m\angle DBF\) \(m\angle FBC=m\angle EBF+m\angle CBE\)	4. Postulado de Adición de Ángulo
5. \(m\angle ABD+m\angle DBF=m\angle EBF+m\angle CBE\)	5. Sustitución PoE
6. \(m\angle ABD+m\angle DBF=m\angle EBF+m\angle ABD\)	6. Sustitución PoE
7. \(m\angle DBF=m\angle EBF\)	7. Resta PoE
8. \(\angle DBF\cong \angle EBF\)	8. Si las medidas son iguales, los ángulos son\ (\ cong.

Ejemplo\(\PageIndex{3}\)

El Teorema de Ángulo Recto establece que si dos ángulos son ángulos rectos, entonces los ángulos son congruentes. Demostrar este teorema.

Para probar este teorema, configura tu propio dibujo y nombra algunos ángulos para que tengas ángulos específicos de los que hablar.

Dado:\(\angle A\) y\(\angle B\) son ángulos rectos

Demostrar:\(\angle A\cong \angle B\)

Solución

*Comunicado*	*Razón*
1. \(\angle A\)y\(\angle B\) son ángulos rectos	1. Dado
2. \(m\angle A=90^{\circ}\)y\(m\angle B=90^{\circ}\)	2. Definición de ángulos rectos
3. \(m\angle A=m\angle B\)	3. PoE Transitivo
4. \(\angle A\cong \angle B\)	4. \(\cong\)ángulos tienen = medidas

Cualquier vez que se mencionen ángulos rectos en una prueba, necesitarás usar este teorema para decir que los ángulos son congruentes.

Ejemplo\(\PageIndex{4}\)

El Teorema de los Suplementos del Mismo Ángulo establece que si dos ángulos son complementarios al mismo ángulo entonces los dos ángulos son congruentes. Demostrar este teorema.

Dado:\(\angle A\) y\(\)\ ángulo B son ángulos suplementarios. \(\angle B\)y\(\angle C\) son ángulos suplementarios.

Demostrar:\(\angle A\cong \angle C\)

Solución

*Comunicado*	*Razón*
1. \(\angle A\)y\(\angle B\) son complementarios \(\angle B\)y\(\angle C\) son complementarios	1. Dado
2. \ (m\ ángulo A+m\ ángulo B=180^ {\ circ} \ (m\ ángulo B+m\ ángulo C=180^ {\ circ}	2. Definición de ángulos suplementarios
3. \(m\angle A+m\angle B=m\angle B+m\angle C\)	3. Sustitución PoE
4. \(m\angle A=m\angle C\)	4. Resta PoE
5. \(\angle A\cong \angle C\)	5. \(\cong\)ángulos tienen = medidas

Ejemplo\(\PageIndex{5}\)

El Teorema de Ángulos Verticales establece que los ángulos verticales son congruentes. Demostrar este teorema.

Dado: Líneas\(k\)\(m\) e intersección.

Demostrar:\(\angle 1\cong \angle 3\)

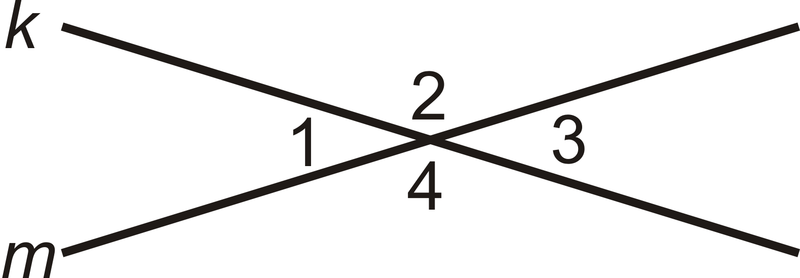
f-d_a48601a6f3b2cacd7454719a7ba6d7cb2e755b3854d83bae8308f3aa+image_tiny+image_tiny.png — Figura\(\PageIndex{5}\)

Solución

*Comunicado*	*Razón*
1. Líneas\(k\)\(m\) e intersección	1. Dado
2. \(\angle 1\)y\(\angle 2\) son un par lineal \(\)\ ángulo 2 y\(\angle 3\) son un par lineal	2. Definición de un par lineal
3. \(\angle 1\)y\(\angle 2\) son complementarios \(\angle 2\)y\(\angle 3\) son complementarios	3. Postulado de Par Lineal
4. \(m\angle 1+m\angle 2=180^{\circ}\) \(m\angle 2+m\angle 3=180^{\circ}\)	4. Definición de ángulos suplementarios
5. \(m\angle 1+m\angle 2=m\angle 2+m\angle 3\)	5. Sustitución PoE
6. \(m\angle 1=m\angle 3\)	6. Resta PoE
7. \(\angle 1\cong \angle 3\)	7. \(\cong\)ángulos tienen = medidas

Ejemplo\(\PageIndex{6}\)

\(\angle 1\cong \angle 4\)y\(\angle C\) y\(\angle F\) son ángulos rectos.

¿Qué ángulos son congruentes y por qué?

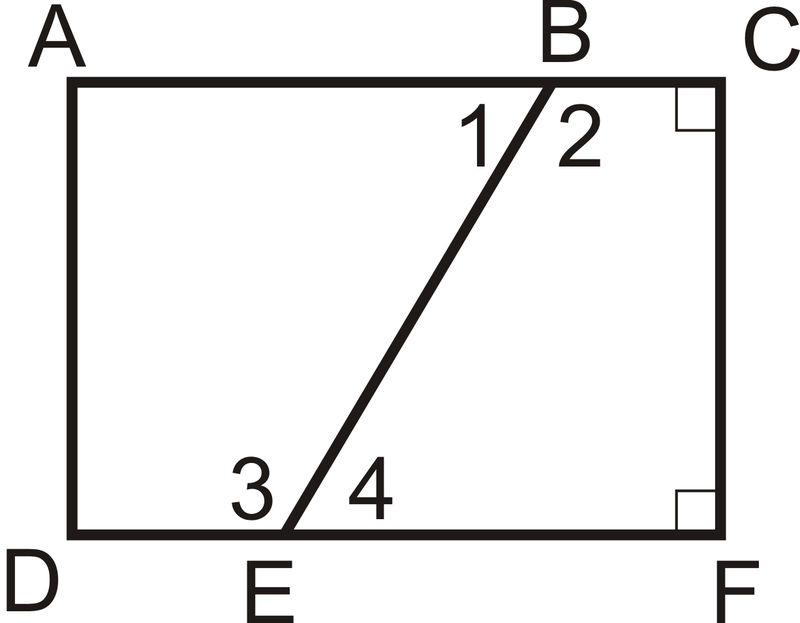
f-d_c1e96ff919536dd8df07b0c96f91127c554c9acb470553431bd23d68+image_tiny+image_tiny.png — Figura\(\PageIndex{6}\)

Solución

Por el teorema de ángulo recto,\(\angle C\cong \angle F\). También,\(\angle 2\cong \angle 3\) por el Teorema de Suplementos de Mismo Ángulos porque\(\angle 1\cong \angle 4\) y son pares lineales con estos ángulos congruentes.

Revisar

Rellene los espacios en blanco en las pruebas a continuación.

Dado:\(\angle ABC\cong \angle DEF\) y\(\angle GHI\cong \angle JKL\)

Demostrar:\(m\angle ABC+m\angle GHI=m\angle DEF+m\angle JKL\)

*Comunicado*	*Razón*
1.	1. Dado
2. \(m\angle ABC=m\angle DEF\) \(m\angle GHI=m\angle JKL\)	2.
3.	3. Adición PoE
4. \(m\angle ABC+m\angle GHI=m\angle DEF+m\angle JKL\)	4.

Dado:\(M\) es el punto medio de\(\overline{AN}\). \(N\)es el punto medio\(\overline{MB}\)

Demostrar:\(AM=NB\)

*Comunicado*	*Razón*
1.	Dado
2.	Definición de un punto medio
3. \(AM=NB\)

Dado:\(\overline{AC}\perp \overline{BD}\) y\(\angle 1\cong \angle 4\)

Demostrar:\(\angle 2\cong \angle 3\)

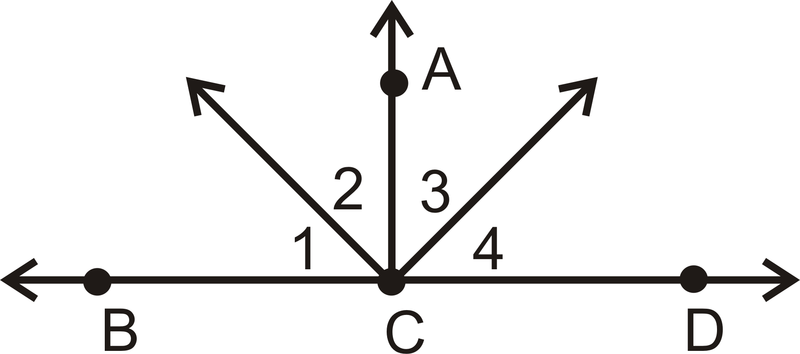
f-d_36fad5a56ee39e8e9e0315b90ea3311e44ed37b1f4e22df1d2728155+image_tiny+imagen_tiny.png — Figura\(\PageIndex{7}\)

*Comunicado*	*Razón*
1. \ (\ overline {AC}\ perp\ overline {BD},\ (\ ángulo 1\ cong\ ángulo 4	1.
2. \(m\angle 1=m\angle 4\)	2.
3.	3. \ (\ líneas perp crean ángulos rectos
4. \(m\angle ACB=90^{\circ}\) \(m\angle ACD=90^{\circ}\)	4.
5. \(m\angle 1+m\angle 2=m\angle ACB\) \(m\angle 3+m\angle 4=m\angle ACD\)	5.
6.	6. Sustitución
7. \(m\angle 1+m\angle 2=m\angle 3+m\angle 4\)	7.
8.	8. Sustitución
9.	9.Resta PoE
10. \(\angle 2\cong \angle 3\)	10.

Dado:\(\angle MLN\cong \angle OLP\)

Demostrar:\(\angle MLO\cong \angle NLP\)

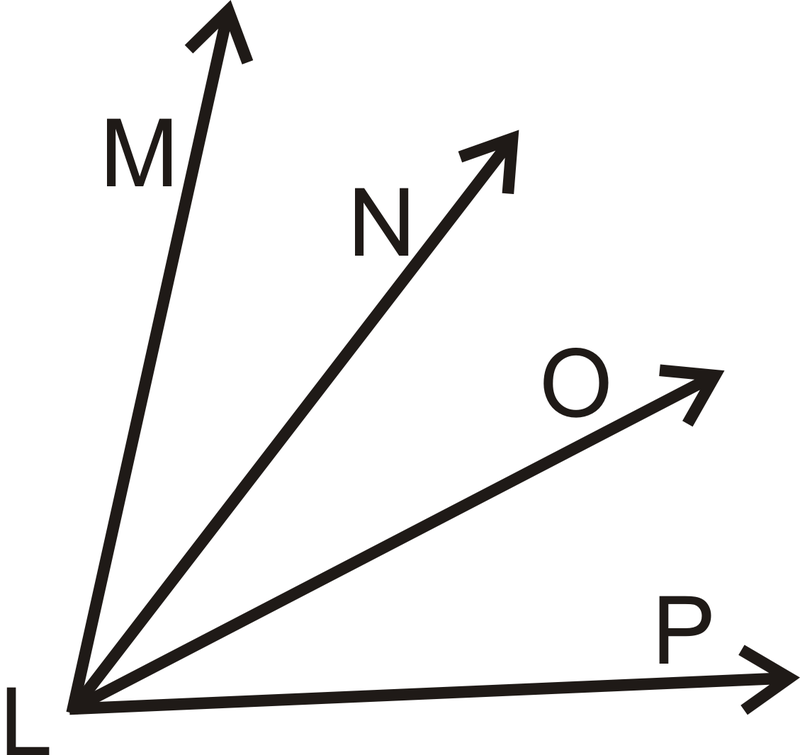
f-d_a02b797babbded430c194906fced340a5bd4a3a321f1ae918792b280+image_tiny+image_tiny.png — Figura\(\PageIndex{8}\)

*Comunicado*	*Razón*
1.	1.
2.	2. \(\cong\)ángulos tienen = medidas
3.	3. Postulado de Adición de Ángulo
4.	4. Sustitución
5. \(m\angle MLO=m\angle NLP\)	5.
6.	6. \(\cong\)ángulos tienen = medidas

Dado:\(\underline{AE}\perp \underline{EC}\) y\(\underline{BE}\perp \underline{ED}\)

Demostrar:\(\angle 1\cong \angle 3\)

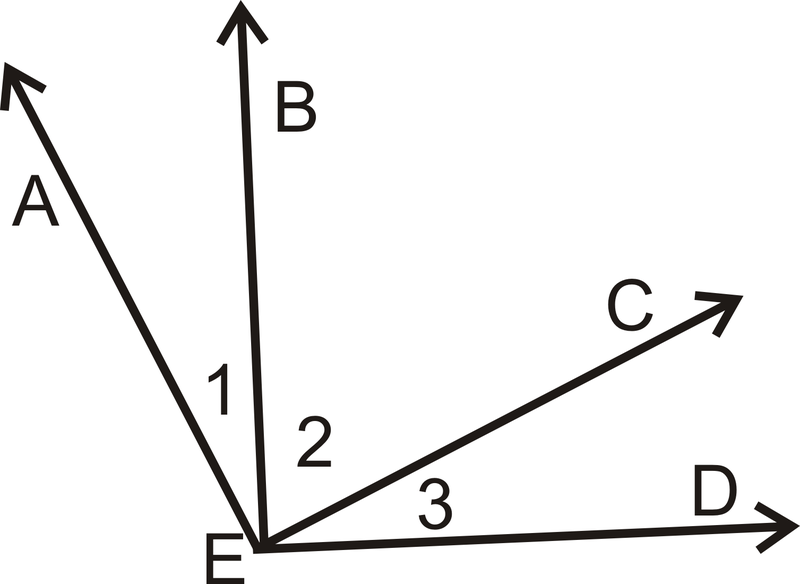
f-d_94f217649976f4a8f1078d9bbe76cff39a1d4aa118a506a28df71050+image_tiny+image_tiny+image_tiny.png — Figura\(\PageIndex{9}\)

*Comunicado*	*Razón*
1.	1.
2.	2. \(\perp\)líneas crean ángulos rectos
3. \(m\angle BED=90^{\circ}\) \(m\angle AEC=90^{\circ}\)	3.
4.	4. Postulado de Adición de Ángulo
5.	5. Sustitución
6. \(m\angle 2+m\angle 3=m\angle 1+m\angle 3\)	6.
7.	7. Resta PoE
8.	8. \(\cong\)ángulos tienen = medidas

Dado:\(\angle L\) es complementario\(\angle M\) y\(\angle P\) es complementario a\(\angle O\) y\(\angle L\cong \angle O\)

Demostrar:\(\angle P\cong \angle M\)

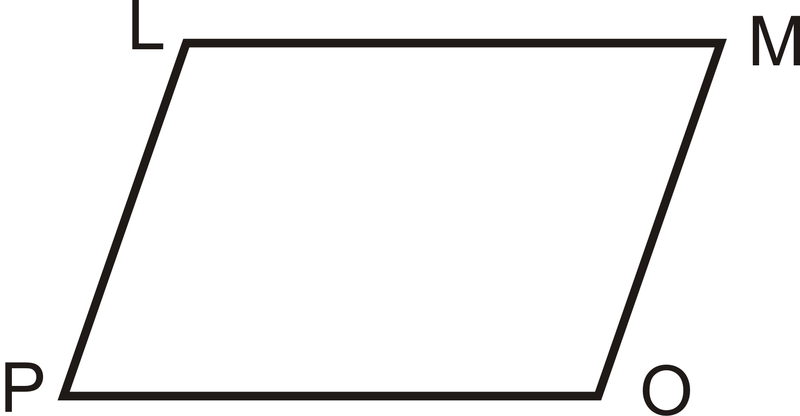
f-d_0b4d4f366f61cc07a6d1cea84e6badc34318936c6aa7919fce3d7bb1+image_tiny+image_tiny.png — Figura\(\PageIndex{10}\)

*Comunicado*	*Razón*
1.	1.
2. \(m\angle L=m\angle O\)	2.
3.	3. Definición de ángulos suplementarios
4.	4. Sustitución
5.	5. Sustitución
6.	6. Resta PoE
7. \(\angle M\cong \angle P\)	7.

Dado:\(\angle 1\cong \angle 4\)

Demostrar:\(\angle 2\cong \angle 3\)

*Comunicado*	*Razón*
1.	1.
2. \(m\angle 1=m\angle 4\)	2.
3.	3. Definición de un par lineal
4. \(\angle 1\)y\(\angle 2\) son complementarios \(\angle 3\)y\(\angle 4\) son complementarios	4.
5.	5. Definición de ángulos suplementarios
6. \(m\angle 1+m\angle 2=m\angle 3+m\angle 4\)	6.
7. \(m\angle 1+m\angle 2=m\angle 3+m\angle 1\)	7.
8. \(m\angle 2=m\angle 3\)	8.
9. \(\angle 2\cong \angle 3\)	9.

Dado:\(\angle C\) y\(\angle F\) son ángulos rectos

Demostrar:\(m\angle C+m\angle F=180^{\circ}\)

*Comunicado*	*Razón*
1.	1.
2. \(m\angle C=90^{\circ}, \(m\angle F=90^{\circ}\)	2.
3. \(90^{\circ}+90^{\circ}=180^{\circ}\)	3.
4. \(m\angle C+m\angle F=180^{\circ}\)	4.

Dado:\(l\perp m\)

Demostrar:\(\angle 1\cong \angle 2\)

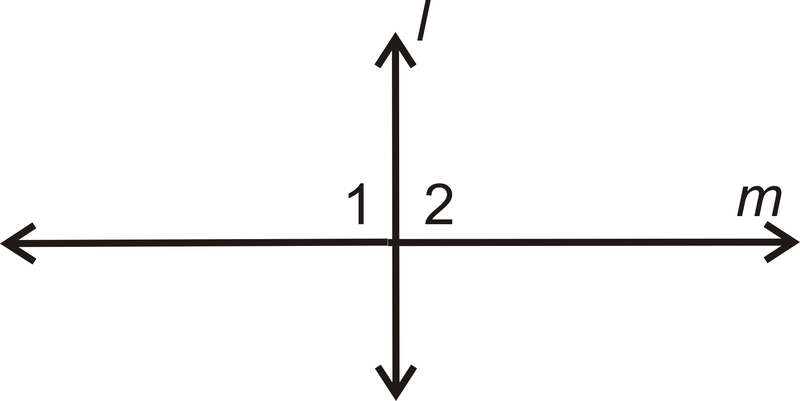
f-d_ce5f73109acc53f5dd286f7726aed3aa0140c001ac46667139ba4050+image_tiny+image_tiny+image_tiny.png — Figura\(\PageIndex{13}\)

*Comunicado*	*Razón*
1. \(l\perp m\)	1.
2. \(\angle 1\)y\(\angle 2\) son ángulos rectos	2.
3.	3.

Dado:\(m\angle 1=90^{\circ}\)

Demostrar:\(m\angle 2=90^{\circ}\)

*Comunicado*	*Razón*
1.	1.
2. \(\angle 1\)y\(\angle 2\) son un par lineal	2.
3.	3. Postulado de Par Lineal
4.	4. Definición de ángulos suplementarios
5.	5. Sustitución
6. \(m\angle 2=90^{\circ}\)	6.

Dado:\(l\perp m\)

Demostrar:\(\angle 1\) y\(\angle 2\) son complementos

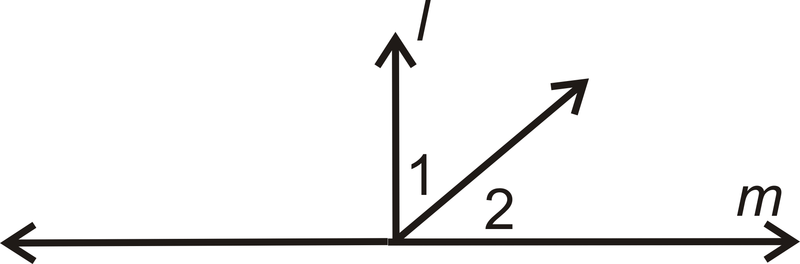
F-D_19042DC8336C54C2F514EA7FE224BA4E011C3F68AFBE52D610BEB138+Image_Tiny+Image_Tiny.png — Figura\(\PageIndex{15}\)

*Comunicado*	*Razón*
1.	1.
2.	2. \(\perp\)líneas crean ángulos rectos
3. \(m\angle 1+m\angle 2=90^{\circ}\)	3.
4. \(\angle 1\)y\(\angle 2\) son complementarios	4.

Dado:\(l\perp m\) y\(\angle 2\cong \angle 6\)

Demostrar:\(\angle 6\cong \angle 5\)

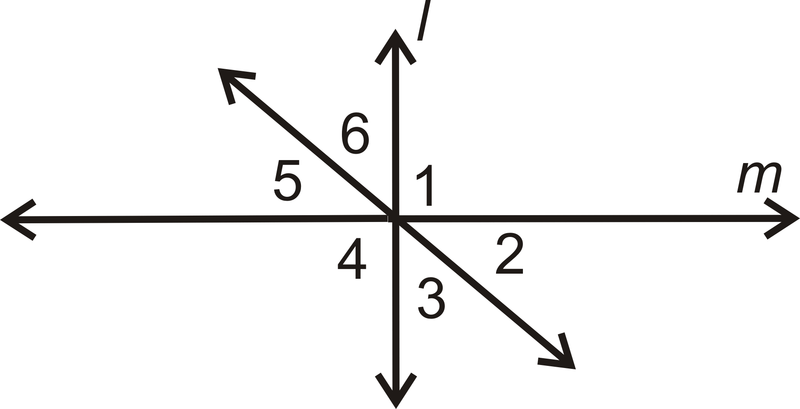
f-d_0a1e84fc5cc3267c7fd61c4636d245ee72029e0e6971870e44ea0bfb+image_tiny+image_tiny.png — Figura\(\PageIndex{16}\)

*Comunicado*	*Razón*
1.	1.
2. \(m\angle 2=m\angle 6\)	2.
3. \(\angle 5\cong \angle 2\)	3.
4. \(m\angle 5=m\angle 2\)	4.
5. \(m\angle 5=m\angle 6\)	5.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.7.

El vocabulario

Término	Definición
prueba de dos columnas	Una forma común de organizar una prueba en geometría. Las pruebas de dos columnas siempre tienen dos columnas- declaraciones y razones.
par lineal	Dos ángulos forman un par lineal si son suplementarios y adyacentes.

Recursos adicionales

Video: Principios de Pruebas de Dos Columnas - Básicos

Actividades: Preguntas de discusión sobre pruebas de dos columnas

Ayudas de estudio: Guía de estudio de pruebas

Práctica: Introducción a las pruebas

Mundo real: Dame una razón

Search

Text Color

Text Size

Margin Size

Font Type