2.17: Pruebas que involucran triángulos
- Page ID
- 107373
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Demostrar teoremas sobre la suma de ángulos, ángulos base de triángulos isósceles y ángulos exteriores e interiores.
Teoremas sobre Triángulos
Recordemos que un triángulo es una forma con exactamente tres lados. Los triángulos se pueden clasificar por sus lados y por sus ángulos.
Al clasificar un triángulo por sus lados, debes mirar para ver si alguno de los lados tiene la misma longitud.
- Si no hay lados de la misma longitud, entonces es un triángulo escaleno.
- Si dos lados tienen la misma longitud, entonces es un triángulo isósceles.
- Si los tres lados tienen la misma longitud, entonces es un triángulo equilátero.

Al clasificar un triángulo por sus ángulos, debe observar el tamaño de los ángulos:
- Si un triángulo tiene un ángulo recto, entonces es un triángulo rectángulo.
- Si las medidas de todos los ángulos en un triángulo son menores que\(90^{\circ}\), entonces es un triángulo agudo.
- Un caso especial de un triángulo agudo es cuando los tres ángulos son iguales. En ese caso, los tres ángulos son de 60 grados, y forman un triángulo equiangular.
- Si la medida de un ángulo en un triángulo es mayor que\(90^{\circ}\), entonces es un triángulo obtuso.

Teorema de suma de triángulo
Demostrar que los ángulos interiores de un triángulo suman a\(180^{\circ}\).
Esta es una propiedad de triángulos de los que has oído hablar y usado antes, pero quizás nunca hayas visto una prueba de por qué es cierto. Aquí hay una prueba de formato de párrafo que se basa en líneas paralelas y ángulos interiores alternos.
Considera el triángulo genérico a continuación.
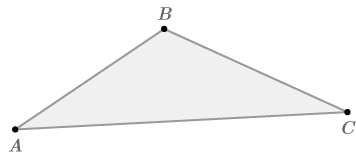
Por el postulado paralelo, existe exactamente una línea paralela a\ overline {AC}\) a través de B\). Dibuja esta línea.

\( \angle DBA\cong \angle A because they are alternate interior angles and alternate interior angles are congruent when lines are parallel. Therefore, \(m\angle DBA=m\angle A\). De igual manera,\(\angle EBC\cong \angle C\) porque también son ángulos interiores alternos, y así\(m\angle EBC=m\angle \). \(m\angle DBA+m\angle ABC+m\angle EBC=180^{\circ}\)porque estos tres ángulos forman una línea recta. Por sustitución,\(m\angle A+m\angle ABC+m\angle C=180^{\circ}\).

La declaración "la suma de las medidas de los ángulos interiores de un triángulo es\(180^{\circ}\)" se conoce como el Teorema de la Suma del Triángulo. Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
Haga clic en la pequeña flecha azul junto a la imagen de abajo y luego arrastre los vértices naranjas para remodelar el triángulo. Observe que la suma de las medidas de los ángulos interiores de un triángulo es siempre\(180^{\circ}\).

Teorema del Triángulo Isósceles
Demostrar que los ángulos base de un triángulo isósceles son congruentes.
Los ángulos base de un triángulo isósceles son los ángulos opuestos a los lados congruentes. Abajo, los ángulos de base están marcados para isósceles\(\Delta ABC\).

Tienes que probarlo\(\angle B\cong \angle C\) dado eso\(\overline{AB}\cong \overline{AC}\). Aquí hay una prueba en el formato de dos columnas, que se basa en bisectores angulares y triángulos congruentes. La prueba hará referencia a la imagen de abajo.

|
Declaraciones |
Razones |
|
Isósceles\(\Delta ABC\) |
Dado |
| \(\overline{AB}\cong \overline{AC}\) |
Definición de triángulo isósceles |
|
Construir\(\overrightleftarrow{AD}\), el ángulo bisectriz de\(\angle A\), con\(F\) la intersección de\(\overline{BC}\) y\(\overrightleftarrow{AD}\) |
Un ángulo tiene solo un ángulo bisectriz |
| \(\overline{AF}\cong \overline{AF}\) |
Propiedad reflexiva |
| \(\angle BAF\cong \angle CAF\) |
Definición de ángulo bisectriz |
|
\(\Delta ABF\cong \Delta ACF\) |
\(SAS\cong\) |
| \(\angle B\cong \angle C\) |
\(CPCTC\) |
La afirmación "los ángulos base de un triángulo isósceles son congruentes" es el Teorema del Triángulo Isósceles. Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
Haga clic en la pequeña flecha azul junto a la imagen de abajo y luego arrastre los vértices naranjas para remodelar el triángulo. Observe que los ángulos base de un triángulo isósceles son siempre congruentes.

Elemento Interactivo
Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Teorema de ángulos exteriores
Demostrar que la medida de un ángulo exterior de un triángulo es igual a la suma de las medidas de los ángulos interiores remotos.
Un ángulo exterior de un triángulo es un ángulo fuera de un triángulo creado extendiendo uno de los lados de los triángulos. Abajo,\(\angle ACD\) se encuentra un ángulo exterior. Para ángulo exterior\(\angle ACD\), los ángulos\(\angle A\) y\(\angle B\) son los ángulos interiores remotos, porque son los ángulos interiores que no son adyacentes al ángulo exterior.

Aquí hay una prueba de diagrama de flujo de este teorema.
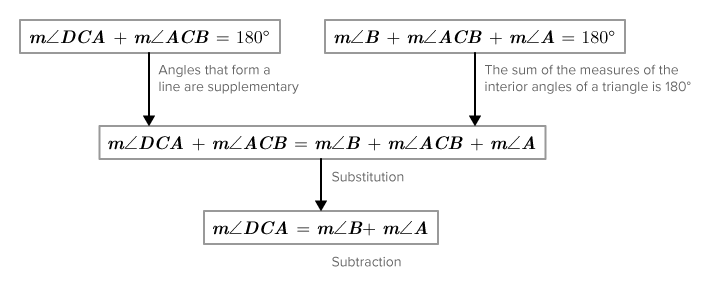
La afirmación “la medida de un ángulo exterior de un triángulo es igual a la suma de las medidas de los ángulos interiores remotos" es el Teorema de Ángulos Exteriores. Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
Haga clic en la pequeña flecha azul junto a la imagen de abajo y luego arrastre los vértices naranjas para remodelar el triángulo. Elija dos ángulos interiores remotos del triángulo y observe cómo la medida de un ángulo exterior permanece igual a la suma de los ángulos interiores remotos.

En el interactivo de abajo, mueve los puntos rojos para cambiar la forma del triángulo. Mueve los puntos azules para comparar los ángulos\ ángulo 1\),\ ángulo 2\), y\ ángulo 3\).
Observe que debido a que son ángulos verticales, los pares de ángulos\(m\angle 1=m\angle 4\)\(m\angle 2=m\angle 5\), y\(m\angle 3=m\angle 6\).
Elemento Interactivo
Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Teorema de Segmento Medio Triángulo
En el triángulo de abajo, el punto D es un punto medio de\(\overline{AC}\) y el punto\(E\) es el punto medio de\(\overline{BC}\). Hacer una conjetura sobre cómo\(\overline{DE}\) se relaciona con\(\overline{AB}\).

Una conjetura es una suposición sobre algo que podría ser cierto. Después de hacer una conjetura, por lo general intentarás demostrarlo. Dos posibles conjeturas son:
- \(\overline{DE} \parallel \overline{AB}\)
- La longitud de\(\overline{DE}\) es la mitad de la longitud de\(\overline{AB}\)
Considera la imagen de abajo.

Para probar la conjetura\ (DE\ paralelo AB, necesitamos probar que\ (\ Delta FEB\ cong\ Delta DEC que luego usamos para probar que\ (BF\ paralelo AC. Luego continuamos con la prueba para probar que\ (\ Delta ADB\ cong\ Delta FBD que luego nos lleva a probar que\ (DE\ paralelo AB.
|
Declaraciones |
Razones |
|
|
1. |
\(\overline{DC}\cong \overline{AD}\),\(\overline{CE}\cong \overline{EB}\),\(\overline{DE}\cong \overline{EF}\) |
Dado |
| \(\angle CED\cong \angle FEB\) |
Los ángulos verticales son congruentes |
|
| \(\Delta FEB\cong \Delta DEC\) | \(SAS\cong\) | |
|
2. |
\(\angle FBE\cong \angle ECD\) |
\(CPCTC\) |
| \(\overline{BF} \parallel \overline{AC}\) |
Si los ángulos interiores alternos son congruentes entonces las líneas son paralelas. |
|
|
3. |
\(\angle ADB\cong \angle DBF\) |
Si las líneas son paralelas, entonces los ángulos interiores alternos son congruentes. |
| \(\overline{DB}\cong \overline{DB}\) |
Propiedad reflexiva |
|
| \(\overline{BF}\cong \overline{DC}\) |
\(CPCTC\) |
|
| \(\overline{BF}\cong \overline{AD}\) |
Sustitución |
|
| \(\Delta ADB\cong \Delta FBD\) | \(SAS\cong\) | |
|
4. |
\(\angle ABD\cong \angle FDB\) |
\(CPCTC\) |
| \(\overline{DE} \parallel \overline{AB}\) |
Si los ángulos interiores alternos son congruentes entonces las líneas son paralelas. |
Aquí está la figura otra vez, para referencia:

Ahora prueba la conjetura de que la longitud de\(DE is half the length of \(AB\).
| Declaraciones | Razones | |
| 5. | \(\overline{DF}\parallel \overline{AB}\) | \(\overline{DE}\)producido en\(F\) |
| \(\overline{BF}\parallel \overline{AD}\) | \(D\)es un punto medio de\(AC\) | |
| \(ABFD\)es un paralelogramo | Definición de un paralelogramo | |
| \(\overline{DE}=\dfrac{1}{2} \overline{DF}\) | \(\overline{DE}\cong \overline{EF}\) | |
| \(\overline{DE}=\dfrac{1}{2} \overline{AB}\) | Definición de un paralelogramo |
Así, el segmento de línea que une los puntos medios de cualquiera de dos lados de un triángulos es paralelo al tercer lado e igual a la mitad del mismo, este es el Teorema del Segmento Medio del Triángulo. Tenga en cuenta que existen otras formas de demostrar que los dos segmentos son paralelos. Un método se basa en triángulos similares, los cuales serán explorados en otro concepto.
Haga clic en la pequeña flecha azul junto a la imagen de abajo y luego arrastre los vértices naranjas para remodelar el triángulo. Observe que el segmento de línea que une los puntos medios de los dos lados de un triángulo es paralelo al tercer lado e igual a la mitad del mismo.

CK-12 PLIX Interactivo
Elemento Interactivo
Revisar
1. Anteriormente, demostró que la suma de los ángulos interiores de un triángulo es\(180^{\circ}\) (el teorema de la suma del triángulo) usando una prueba de párrafo. Ahora, reescribe esta prueba en el formato de dos columnas.
2. Vuelva a escribir la prueba del Teorema de la Suma Triangular, esta vez en el formato de diagrama de flujo.
3. Anteriormente, demostró que los ángulos base de un triángulo isósceles son congruentes usando una prueba de dos columnas. Ahora, reescribe esta prueba en el formato de párrafo.
4. Vuelva a escribir el teorema del triángulo isósceles, esta vez en el formato de diagrama de flujo.
5. Anteriormente, demostró que la medida de un ángulo exterior de un triángulo es igual a la suma de las medidas de los ángulos interiores remotos utilizando el formato de diagrama de flujo. Ahora, reescribe esta prueba en el formato de párrafo.
6. Vuelva a escribir la prueba de ángulos exteriores, esta vez en el formato de dos columnas.
7. Recordemos que el segmento que une puntos medios de dos lados de un triángulo es paralelo al tercer lado del triángulo. Dado el diagrama a continuación y que\(\Delta ADB\cong \Delta FBD\) como se demostró anteriormente en la lección, demuéstralo\(DE=\dfrac{1}{2} AB\).
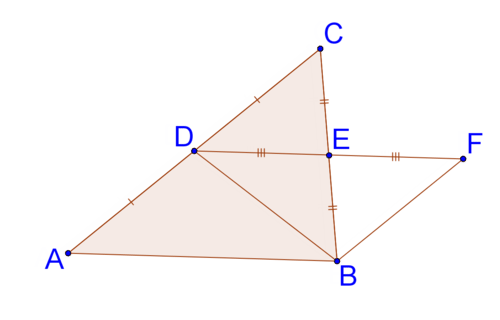
8. ¿Cuál es lo contrario de: “si un triángulo es isósceles, los ángulos de base son congruentes?” ¿Por qué crees que lo contrario también es cierto o no es cierto?
9. Demostrar que si dos ángulos de un triángulo son congruentes, entonces el triángulo es isósceles. Utilice el diagrama y la prueba de dos columnas a continuación y rellene los espacios en blanco para completar la prueba.
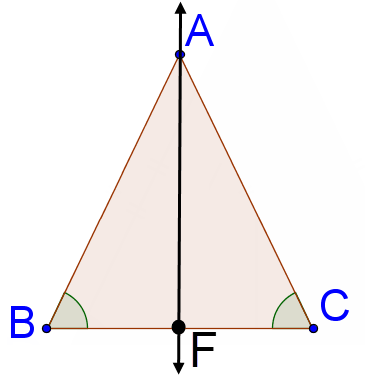
|
Declaraciones |
Razones |
| \(\angle B\cong \angle C\) |
________ |
|
Construir\(\overrightleftarrow{AF}\), el ángulo bisectriz de\(\angle A\), con\(F\) la intersección de\(\overline{BC}\) y\(\overrightleftarrow{AF}\) |
Un ángulo tiene solo un ángulo bisectriz |
| ________ |
Definición de ángulo bisectriz |
|
________ |
Propiedad reflexiva |
| \(\Delta ABF\cong \Delta ACF\) | ________ |
| ________ |
\(CPCTC\) |
10. Reescribe la prueba de que un triángulo con dos ángulos congruentes es isósceles en el formato de diagrama de flujo.
11. Reescribir la prueba del triángulo isósceles en el formato de párrafo.
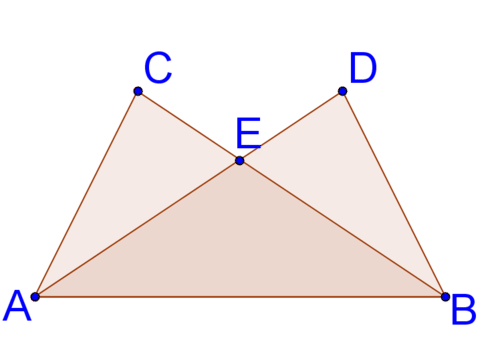
12. Dado eso\(\Delta ABC\cong \Delta BAD\), demostrar que\(\Delta AEB\) es isósceles.
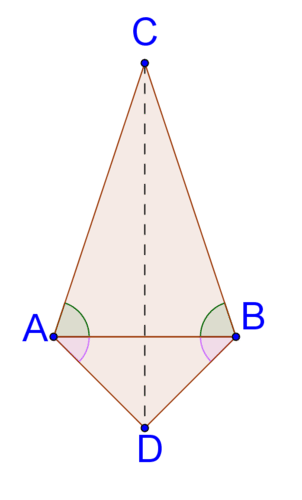
13. Dadas las marcas en la imagen de abajo, explicar por qué\(\overline{CD}\) es la bisectriz perpendicular de\(\overline{AB}\).
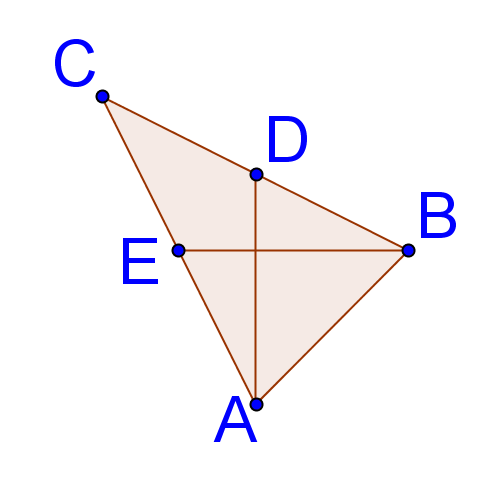
14. En la imagen de abajo,\(\Delta ABC is isosceles with \(\overline{AC}\cong \overline{CB}\). \(E\)es el punto medio de\(\overline{AC}\) y\(D\) es el punto medio de\(\overline{CB}\). \(\Delta EAB\cong \Delta DBA\)Demuéstralo.
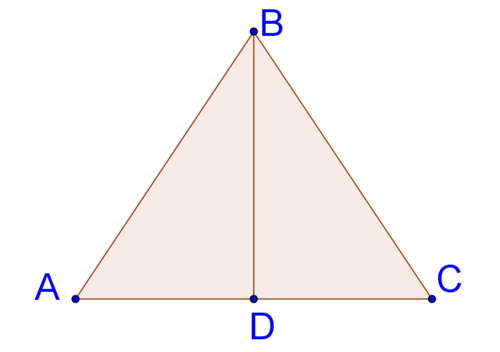
15. Explicar por qué saber que\(\DeltaABC\) es isósceles no es suficiente información para demostrarlo\(\DeltaABD\cong \DeltaCBD\).
16 Dado:\(\angle CBD\cong \angle EFD\);\(\overline{CB}\cong \overline{EF}\)
Demostrar:\(\angle DBF\cong \angle DFB\)

17. Dado:\(\overline{BC}\cong \overline{EF}\);\(\overline{CF}\cong \overline{EB}\)
Demostrar:\(\Delta BDF\) es isósceles
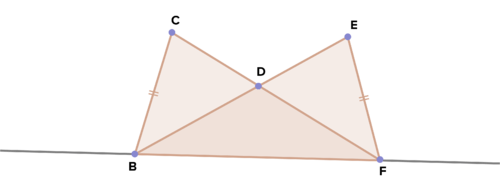
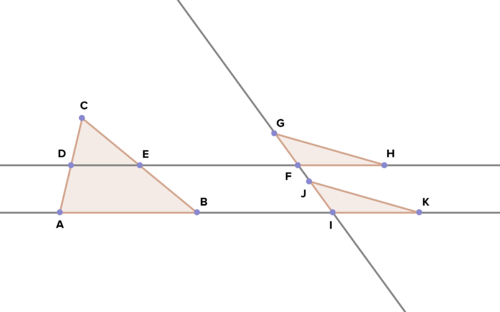
18. Dado:\(\overline{DE}\) segmento medio de\(\Delta ABC \);\(\overline{GF}\cong \overline{JI}\);\(\overline{FH}\cong \overline{IK}\)
Demostrar:\(\Delta GFH \cong \Delta JIK\)
Reseña (Respuestas)
Para ver las respuestas de la opinión, haga clic aquí.
Recursos adicionales
Elemento Interactivo
Práctica: Pruebas que involucran triángulos

