3.9: Líneas paralelas en el plano de coordenadas
- Page ID
- 107402
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Líneas con la misma pendiente que nunca se cruzan.
Las líneas paralelas son dos líneas que nunca se cruzan. En el plano de coordenadas, eso se vería así:
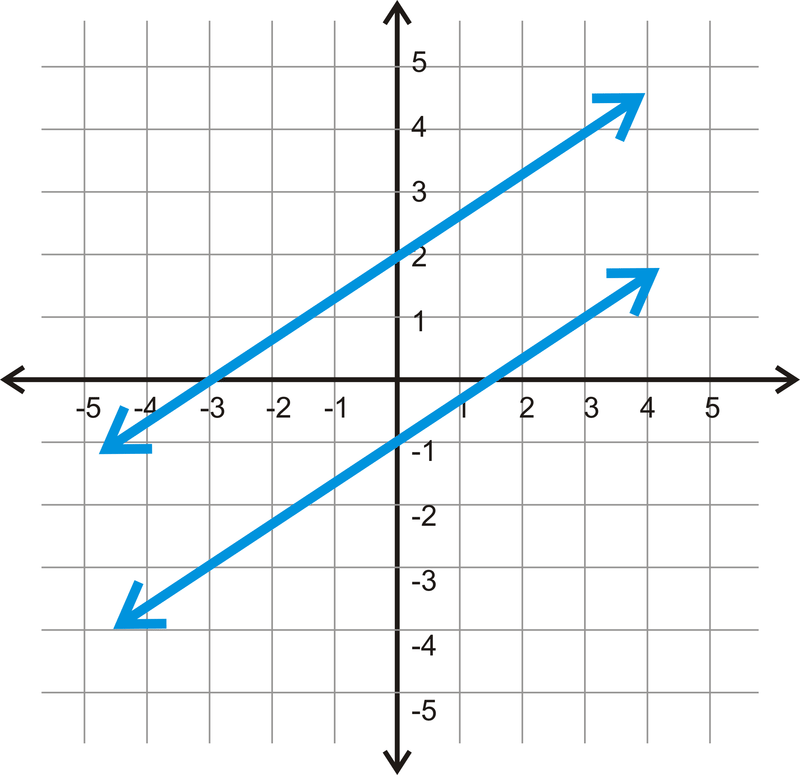
Si echamos un vistazo más de cerca a estas dos líneas, las pendientes son ambas\(\dfrac{2}{3}\).
Esto puede generalizarse a cualquier par de líneas paralelas. Las líneas paralelas siempre tienen la misma pendiente y diferentes\(y\) −intercepciones.
¿Y si te dieran dos líneas paralelas en el plano de coordenadas? ¿Qué podrías decir de sus pistas?
Video
Ejemplo\(\PageIndex{1}\)
Encuentra la ecuación de la línea que es paralela\(y=\dfrac{1}{4}x+3\) y que pasa por ella\((8, -7)\).
Solución
Sabemos que las líneas paralelas tienen la misma pendiente, por lo que la línea tendrá una pendiente de\(dfrac{1}{4}\). Ahora, tenemos que encontrar el\(y\) −intercept. Enchufe 8 para x y -7 para resolver\(y\) para el nuevo\(y\) −intercept (b).
\(\begin{align*}−7=\dfrac{1}{4} (8)+b \\ −7&=2+b \\ −9 &=b \end{align*}\)
La ecuación de la línea paralela es\(y=\dfrac{1}{4}x−9\).
Ejemplo\(\PageIndex{2}\)
¿Son las líneas\(3x+4y=7\) y\(y=\dfrac{3}{4} x+1\) paralelas?
Solución
Primero necesitamos reescribir la primera ecuación en forma de pendiente-intercepción.
\(\begin{align*}3x+4y &=7 \\ 4y &=−3x+7 \\ y &=−\dfrac{3}{4}x+\dfrac{7}{4} \end{align*}\).
La pendiente de esta línea es\(−\dfrac{3}{4}\) mientras que la pendiente de la otra línea es\(\dfrac{3}{4}\). Debido a que las pendientes son diferentes las líneas no son paralelas.
Ejemplo\(\PageIndex{3}\)
Encuentra la ecuación de la línea que es paralela\(y=−\dfrac{1}{3} x+4\) y que pasa por ella\((9, -5)\).
Solución
Recordemos que la ecuación de una línea es y=mx+b, donde m es la pendiente y b es la\(y\) intersección −. Sabemos que las líneas paralelas tienen la misma pendiente, por lo que la línea tendrá una pendiente de −13. Ahora, tenemos que encontrar el\(y\) −intercept. Enchufe 9 para\(x\) y -5 para resolver\(y\) para el nuevo\(y\) −intercept (b).
\(\begin{align*}−5&=−\dfrac{1}{3} (9)+b \\ −5&=−3+b \\−2&=b\end{align*}\)
La ecuación de línea paralela es\(y=−\dfrac{1}{3} x−2\).
Ejemplo\(\PageIndex{4}\)
Encuentra la ecuación de las líneas a continuación y determina si son paralelas.
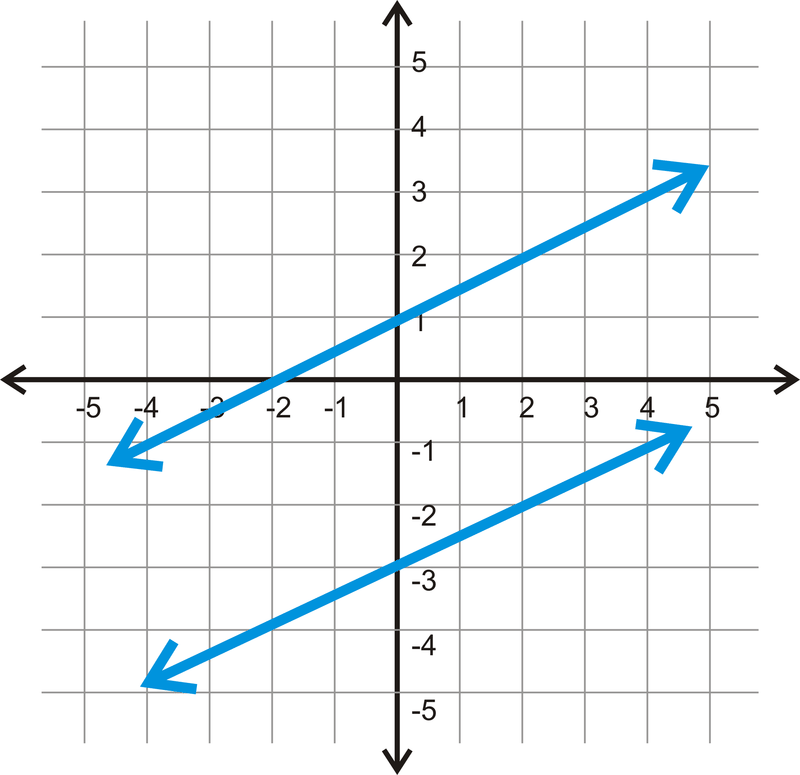
Solución
La línea superior tiene un\(y\) −intercept de 1. A partir de ahí, usa “subir sobre carrera” para encontrar la pendiente. Desde el\(y\) −intercept, si subes 1 y más 2, vuelves a golpear la línea,\(m=\dfrac{1}{2}\). La ecuación es\(y=\dfrac{1}{2} x+1\).
Para la segunda línea, el\(y\) −intercept es -3. La “subida” es 1 y la “carrera” es 2 haciendo la pendiente\(\dfrac{1}{2}\). La ecuación de esta línea es\(y=\dfrac{1}{2} x−3\).
Las líneas son paralelas porque tienen la misma pendiente.
Ejemplo\(\PageIndex{5}\)
Encuentra la ecuación de la línea que es paralela a la línea a través del punto marcado con un punto azul.
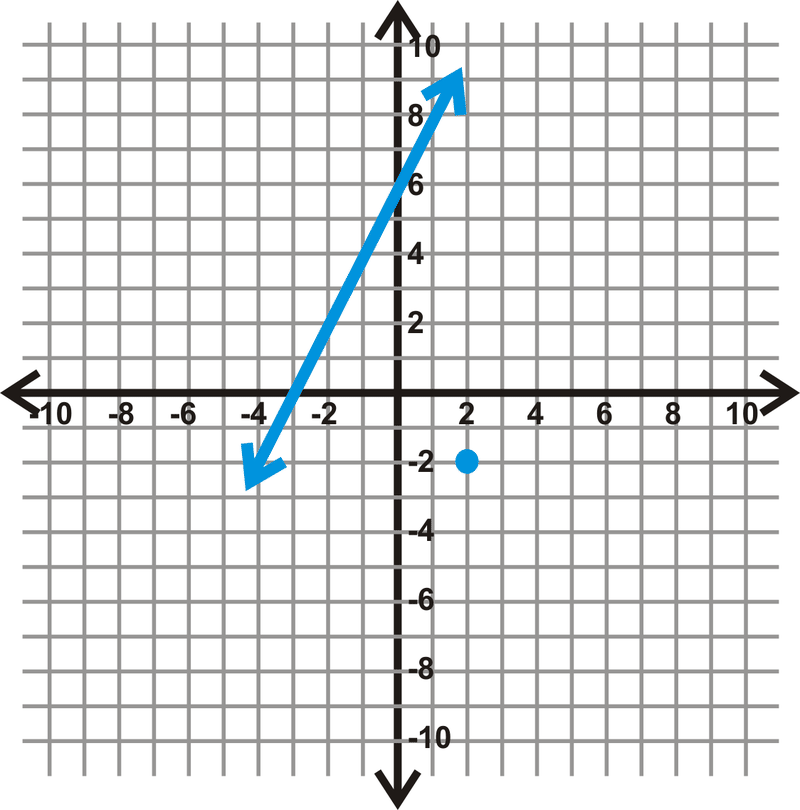
Solución
Primero, observe que la ecuación de la línea es\(y=2x+6\) y el punto es\((2, -2)\). El paralelo tendría la misma pendiente y pasaría a través\((2, -2)\).
\(\begin{align*}y &=2x+b \\ −2 &=2(2)+b \\ −2&=4+b \\−6&=b \end{align*}\)
La ecuación de la línea paralela es\(y=2x+−6\).
Revisar
Determina si cada par de líneas son paralelas. Después, grafica cada par en el mismo conjunto de ejes.
- \(y=4x−2\)y\(y=4x+5\)
- \(y=−x+5\)y\(y=x+1\)
- \(5x+2y=−4\)y\(5x+2y=8\)
- \(x+y=6\)y\(4x+4y=−16\)
Determinar la ecuación de la línea que es paralela a la línea dada, a través del punto dado.
- \(y=−5x+1; (−2,3)\)
- \(y=\dfrac{2}{3}x−2; (9,1)\)
- \(x−4y=12; (−16,−2)\)
- \(3x+2y=10; (8,−11)\)
Encuentra la ecuación de las dos líneas en cada gráfica a continuación. Entonces, determine si las dos líneas son paralelas.
-
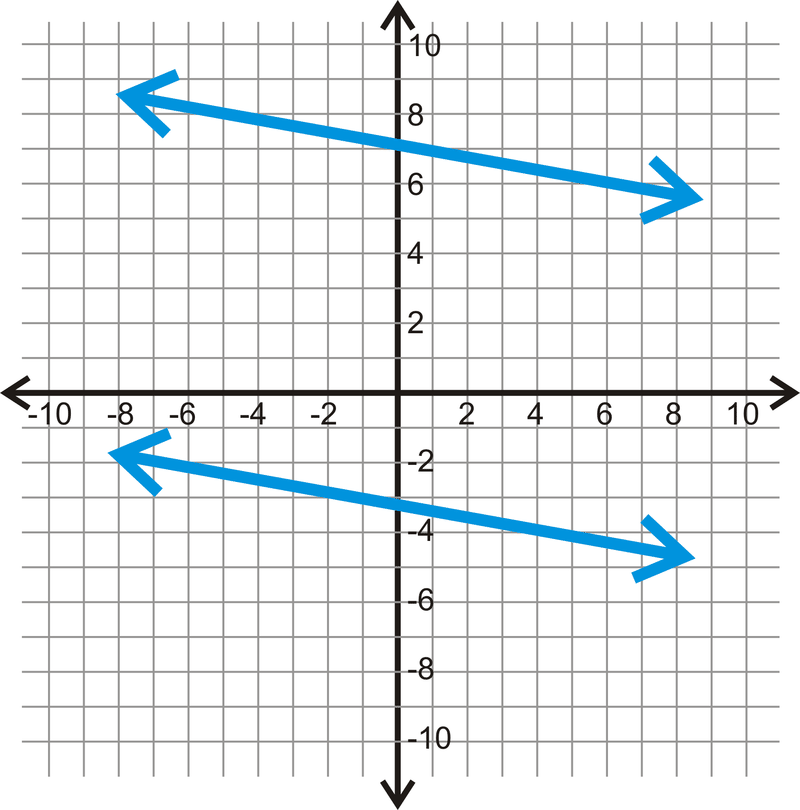
Figura\(\PageIndex{4}\)
Para la línea y el punto de abajo, busque una línea paralela, a través del punto dado.
-
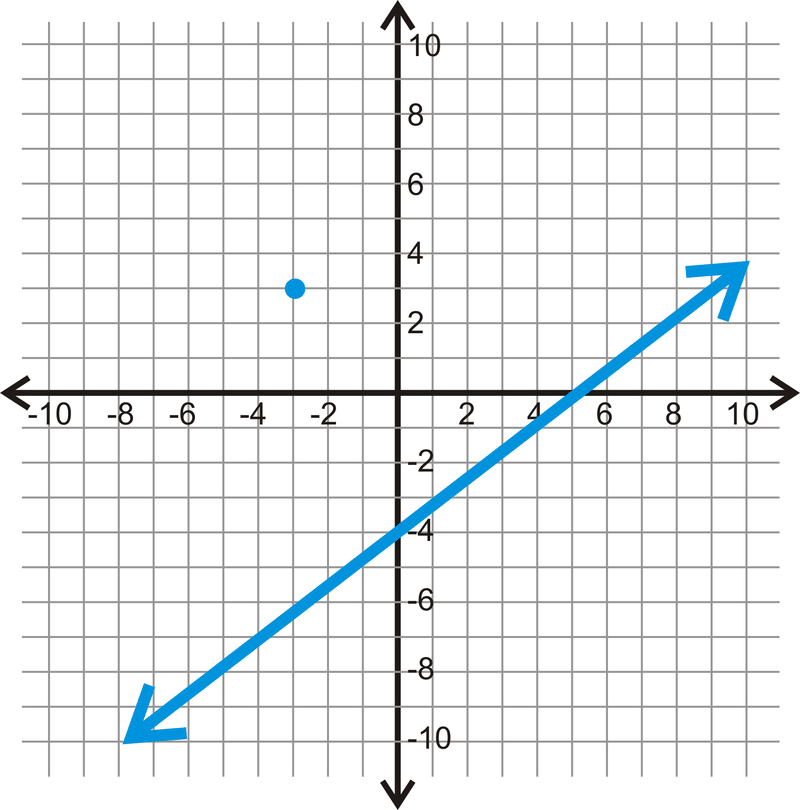
Figura\(\PageIndex{5}\) -
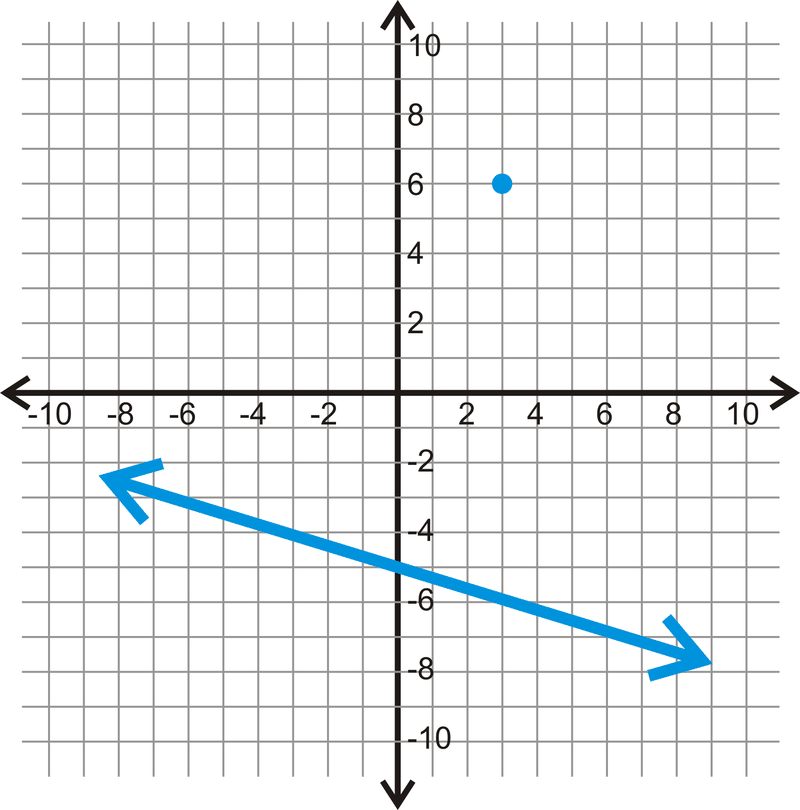
Figura\(\PageIndex{6}\) -
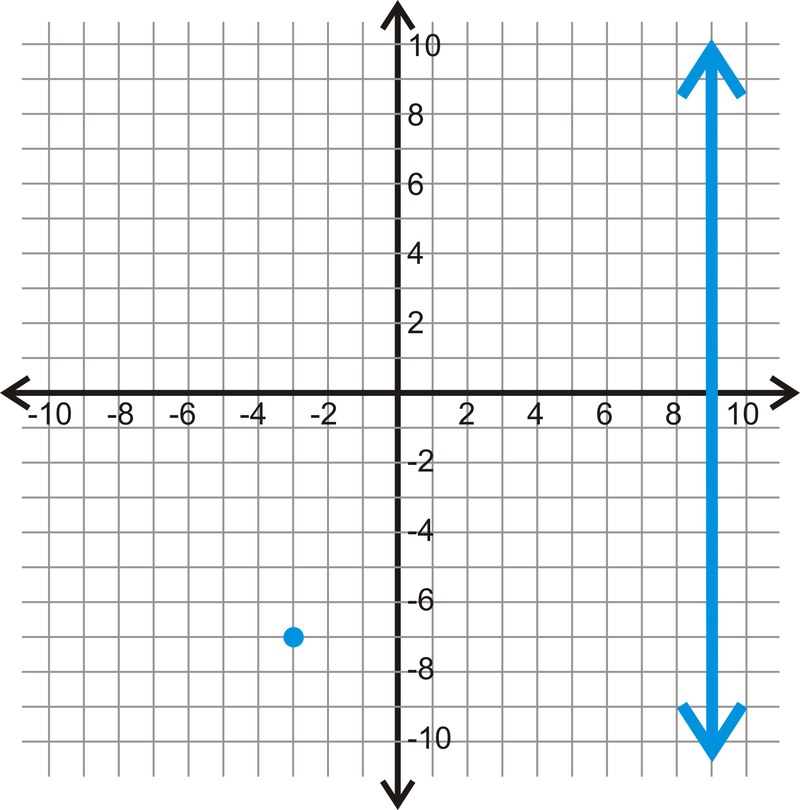
Figura\(\PageIndex{7}\) -
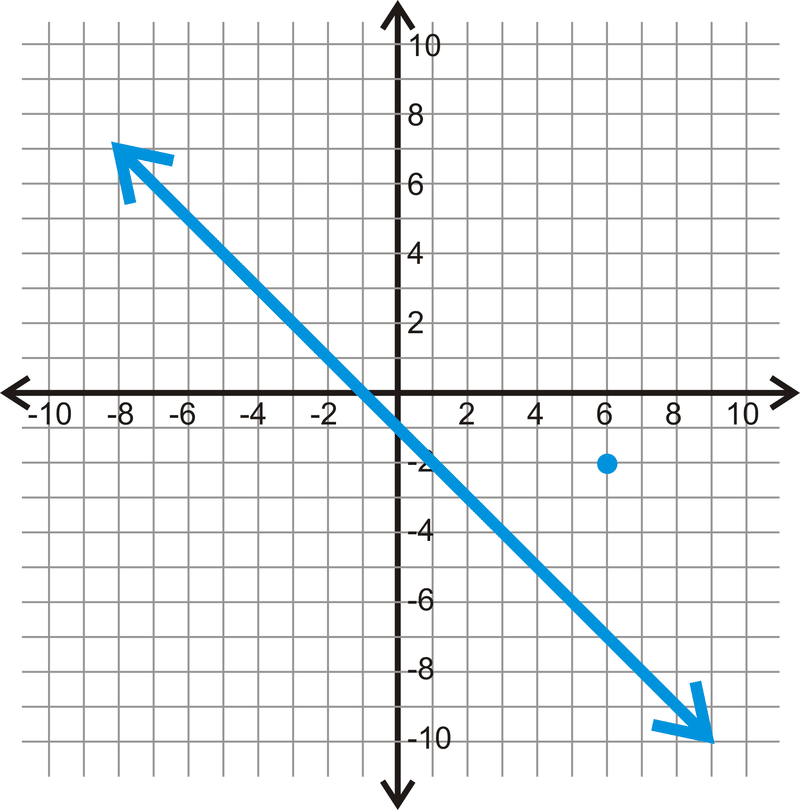
Figura\(\PageIndex{8}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.8.
El vocabulario
| Término | Definición |
|---|---|
| Paralelo | Dos o más líneas son paralelas cuando se encuentran en el mismo plano y nunca se cruzan. Estas líneas siempre tendrán la misma pendiente. |
Recurso Adicional
Elemento Interactivo
Video: Ecuaciones de líneas paralelas y perpendiculares
Actividades: Líneas paralelas en el plano coordinado Preguntas de discusión
Ayudas de estudio: Líneas en el plano de coordenadas
Práctica: Líneas paralelas en el plano de coordenadas
Mundo Real: Líneas Paralelas en el Plano Coordiante