3.8: Ángulos y líneas perpendiculares
- Page ID
- 107371
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Líneas que se cruzan a 90 grados o ángulo recto.
Dos líneas son perpendiculares cuando se cruzan para formar un\(90^{\circ}\) ángulo. Abajo,\(l\perp \overline{AB}\).
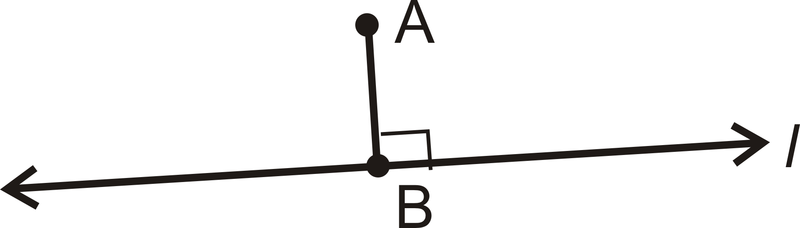
En la definición de perpendicular se utiliza la palabra “línea”. Sin embargo, los segmentos de línea, rayos y planos también pueden ser perpendiculares. La siguiente imagen muestra dos planos paralelos, con un tercer plano azul que es perpendicular a ambos.
Datos básicos sobre las líneas perpendiculares
Teorema #1: Si\(l\parallel m\) y\(n\perp l\), entonces\(n\perp m\).
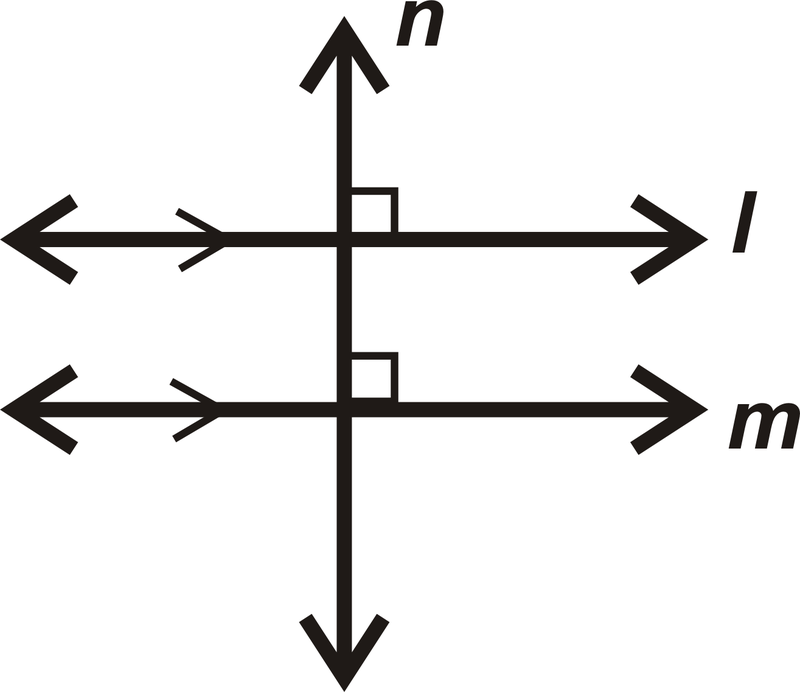
Teorema #2: Si\(l\perp n\) y\(n\perp m\), entonces\(l\parallel m\).
Postulado: Para cualquier línea y un punto que no esté en la línea, hay una línea perpendicular a esta línea que pasa por el punto. Hay infinitamente muchas líneas que pasan por ellas\(A\), pero sólo una que es perpendicular a\(l\).
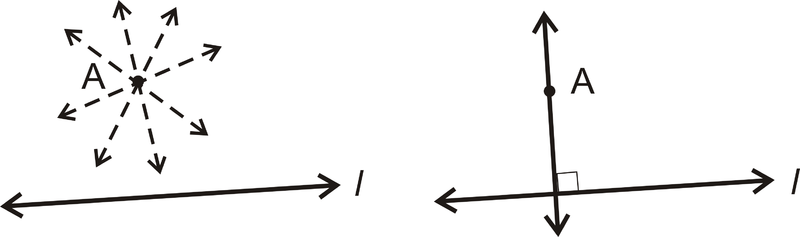
¿Y si te dieran un par de líneas que se cruzan entre sí en\(90^{\circ}\) ángulo? ¿Qué terminología usaría para describir tales líneas?
Ejemplo\(\PageIndex{1}\)
Determinar la medida de\(\angle 1\).
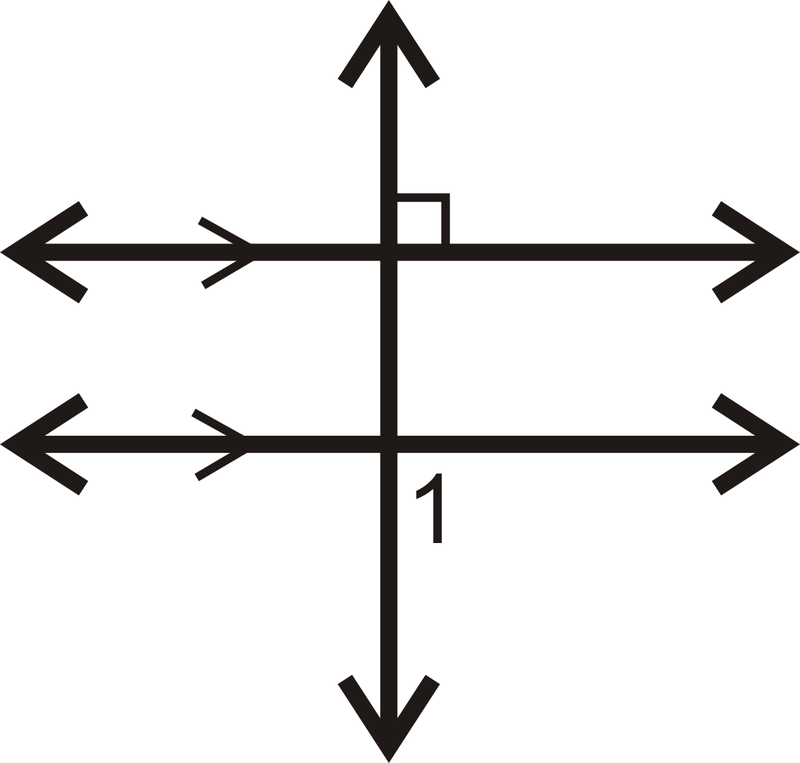
Solución
Sabemos que ambas líneas paralelas son perpendiculares a la transversal.
\(m\angle 1=90^{\circ}\).
Ejemplo\(\PageIndex{2}\)
Encuentra\(m\angle 1\).
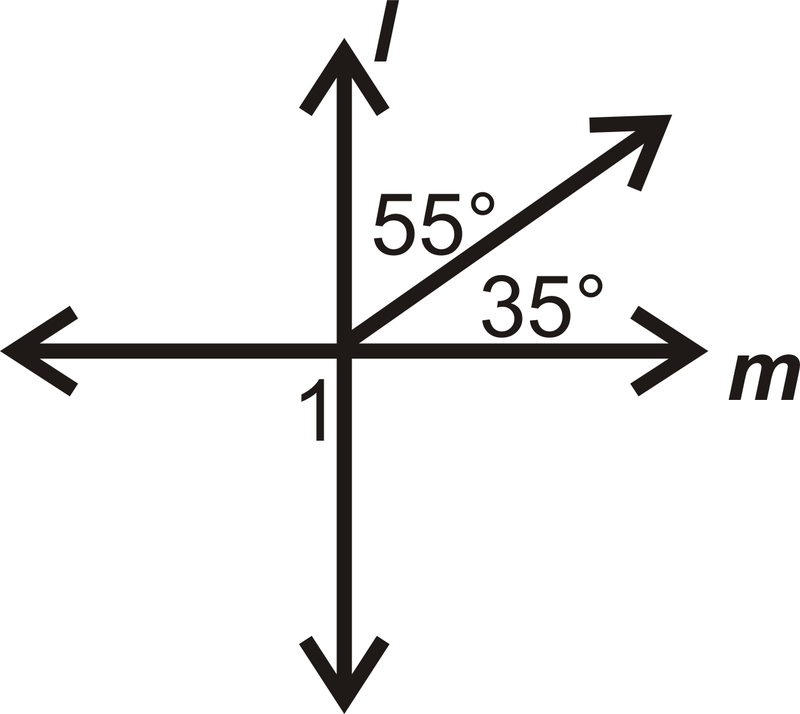
Solución
Los dos ángulos adyacentes se suman a\(90^{\circ}\), entonces\(l\perp m\).
\(m\angle 1=90^{\circ}\)
porque es un ángulo vertical con respecto al par de ángulos adyacentes y los ángulos verticales son congruentes.
Ejemplo\(\PageIndex{3}\)
¿Cuál de los siguientes es el mejor ejemplo de líneas perpendiculares: Latitud en un globo, lados opuestos de un marco de fotos, postes de cercas o lados adyacentes de un marco de fotos?
Solución
El mejor ejemplo serían los lados adyacentes de un marco de fotos. Recuerda que adyacente significa al lado y compartir un vértice. Los lados adyacentes de un marco de fotos se encuentran en\(90^{\circ}\) ángulo y por lo tanto estos lados son perpendiculares.
Ejemplo\(\PageIndex{4}\)
¿Es\(\overleftrightarrow{SO} \perp \overrightarrow{GD}\)?
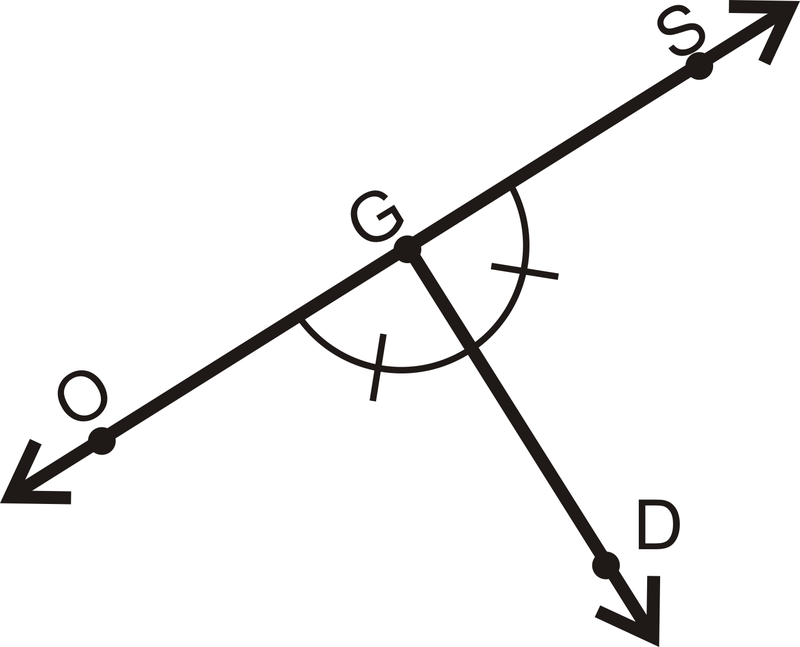
Solución
\(\angle OGD\cong \angle SGD\)y los ángulos forman un par lineal. Esto significa que ambos ángulos son\(90^{\circ}\), por lo que las líneas son perpendiculares.
Ejemplo\(\PageIndex{5}\)
Escribir una prueba de 2 columnas para probar el Teorema #1. Nota: Es necesario comprender los ángulos correspondientes para poder entender esta prueba. Si aún no has aprendido los ángulos correspondientes, asegúrate de revisar primero ese concepto, o saltarte este ejemplo por ahora.
Dado:\(l\parallel m\),\(l\perp n\)
Demostrar:\(n\perp m\)
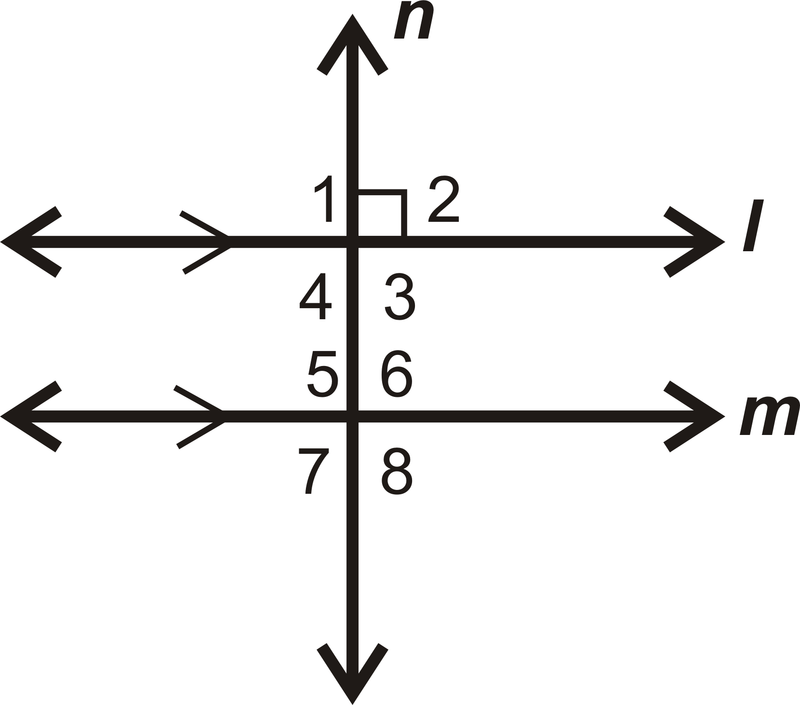
Solución
| Declaración | Razón |
|---|---|
| 1. \(l\parallel m\),\(l\perp n\) | 1. Dado |
| 2. \(\angle 1\),\(\angle 2\),\(\angle 3\), y\(\angle 4 are right angles\) | 2. Definición de líneas perpendiculares |
| 3. \(m\angle 1=90^{\circ}\) | 3. Definición de un ángulo recto |
| 4. \(m\angle 1=m\angle 5\) | 4. Postulado de ángulos correspondientes |
| 5. \(m\angle 5=90^{\circ}\) | 5. Transitivo\(PoE\) |
| 6. \(m\angle 6=m\angle 7=90^{\circ}\) | 6. Pares Lineales Congruentes |
| 7. \(m\angle 8=\(90^{\circ}\) | 7. Teorema de ángulos verticales |
| 8. \(\angle 5\),\(\angle 6\)\(\angle 7\), y\(\angle 8\) son ángulos rectos | 8. Definición de ángulo recto |
| 9. \(n\perp m\) | 9. Definición de líneas perpendiculares |
Revisar
Utilice la siguiente figura para responder a las preguntas 1-2. Los dos pentágonos son paralelos y todos los lados rectangulares son perpendiculares a ambos.
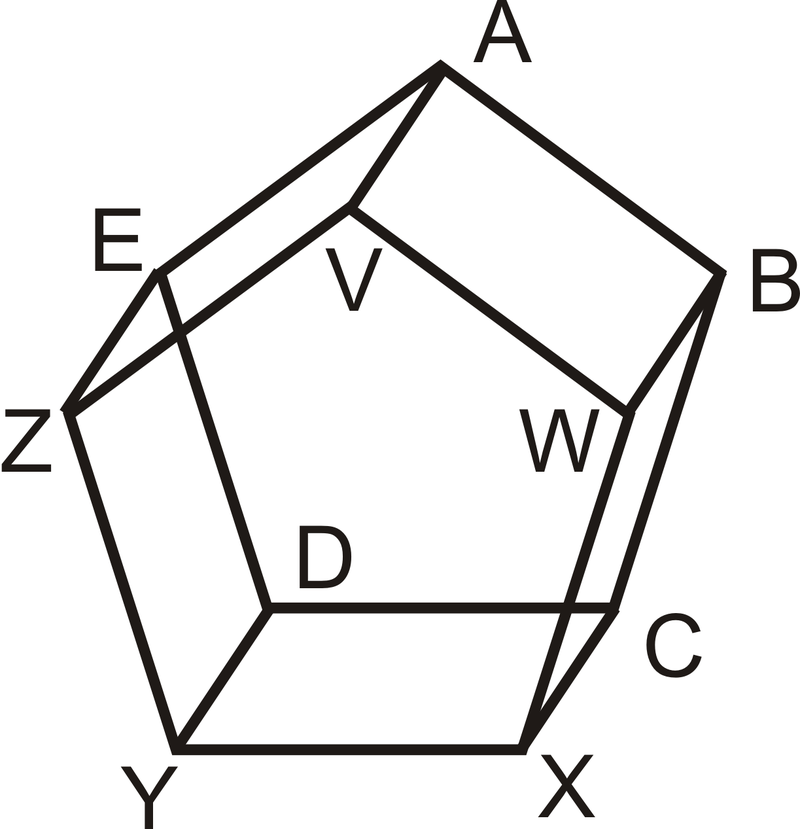
- Enumere un par de líneas perpendiculares.
- Porque\(\overline{AB}\), ¿cuántas líneas perpendiculares pasarían por punto\(V\)? Nombra esta (s) línea (s).
Usa la imagen de abajo para la pregunta 3.
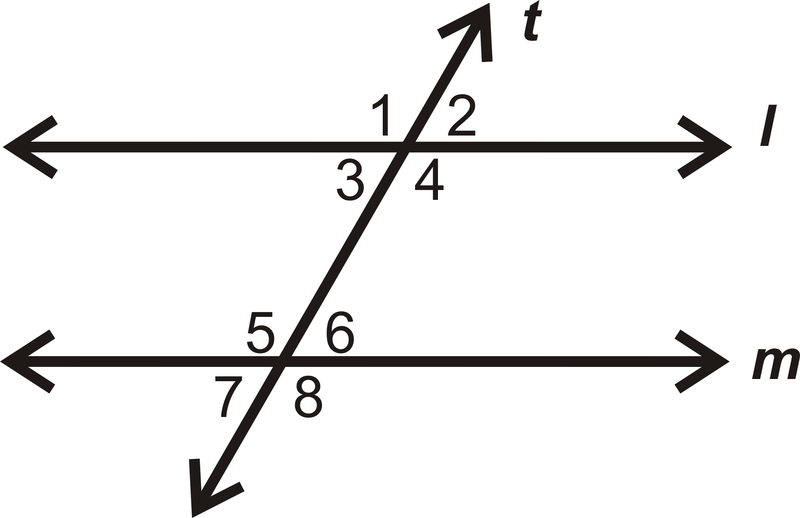
- Si\(t\perp l\), ¿es\(t\perp m\)? ¿Por qué o por qué no?
Encuentre la medida de\(\angle 1\) para cada problema a continuación.
-
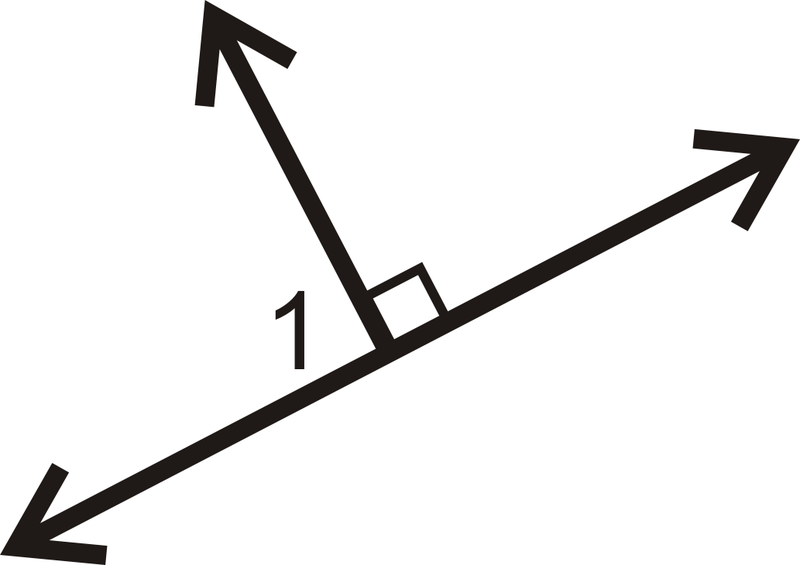
Figura\(\PageIndex{12}\) -
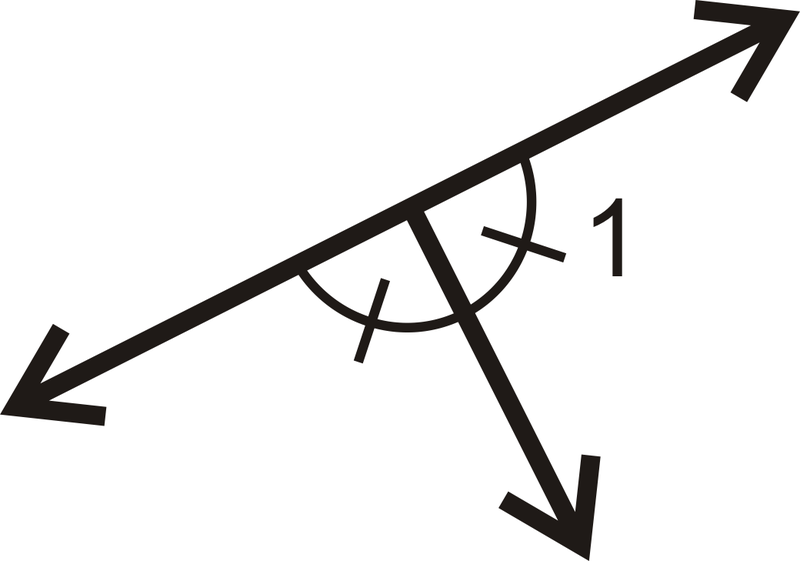
Figura\(\PageIndex{13}\) -
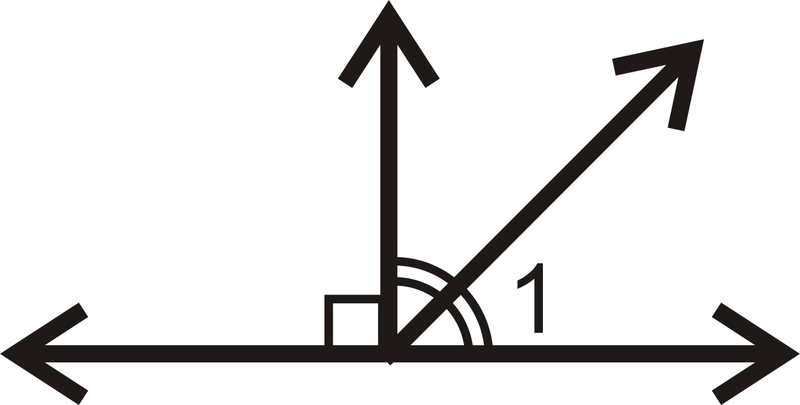
Figura\(\PageIndex{14}\) -
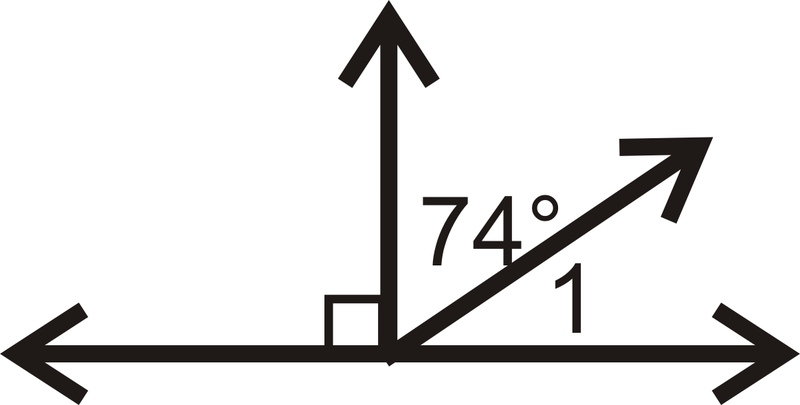
Figura\(\PageIndex{15}\) -
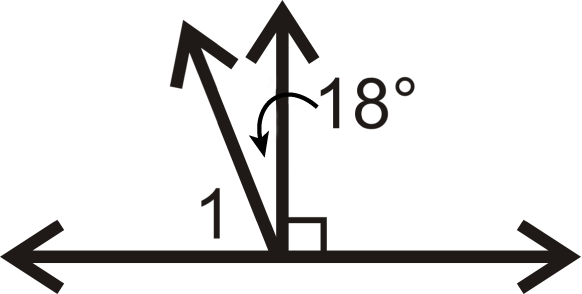
Figura\(\PageIndex{16}\) -
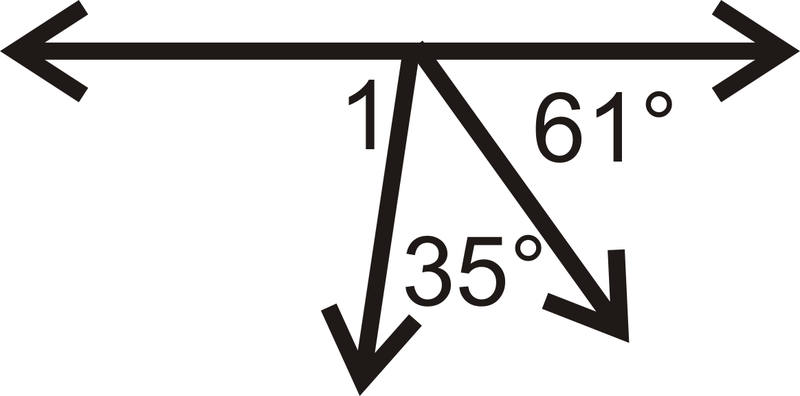
Figura\(\PageIndex{17}\) -
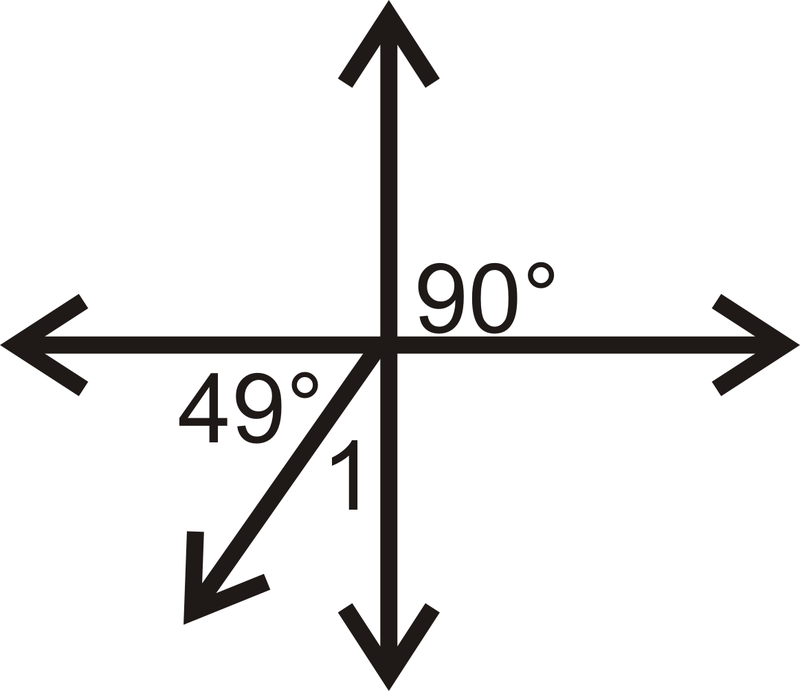
Figura\(\PageIndex{18}\) -
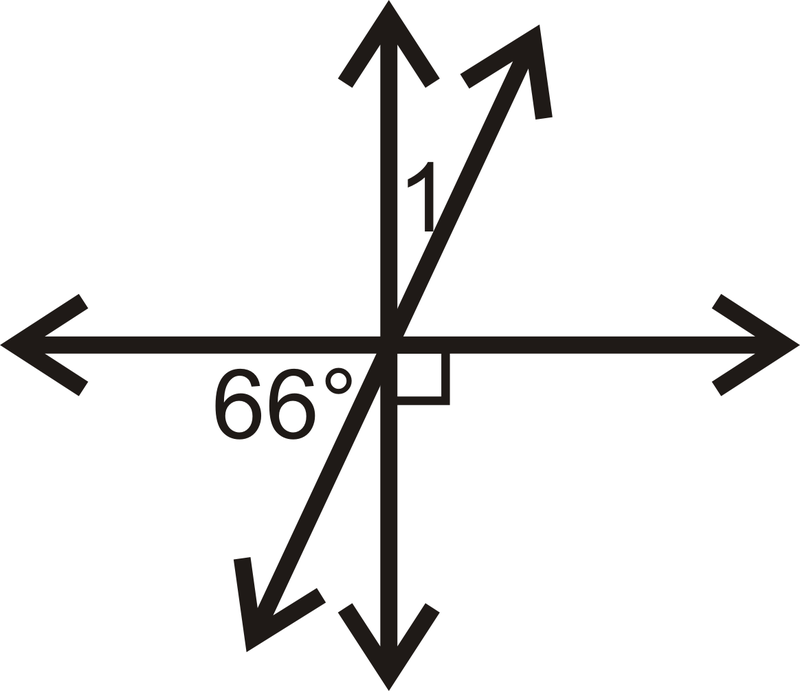
Figura\(\PageIndex{19}\) -
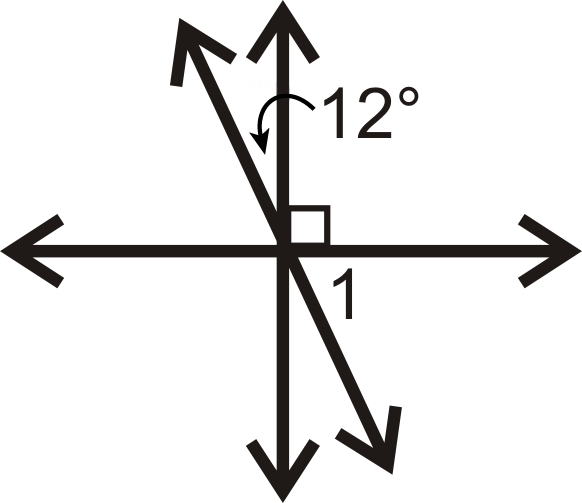
Figura\(\PageIndex{20}\)
En las preguntas 13-16, determinar si\(l\perp m.\)
-
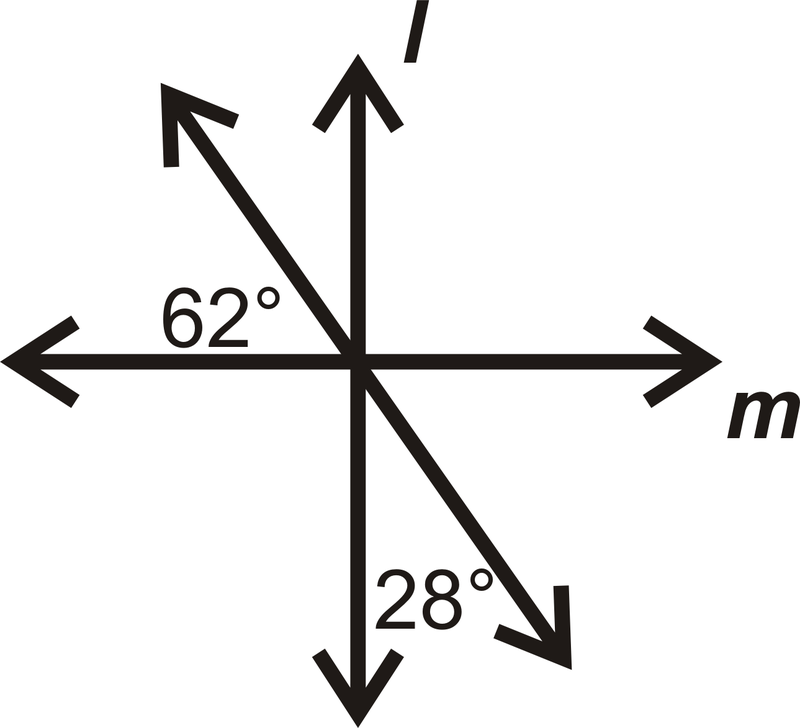
Figura\(\PageIndex{21}\) -
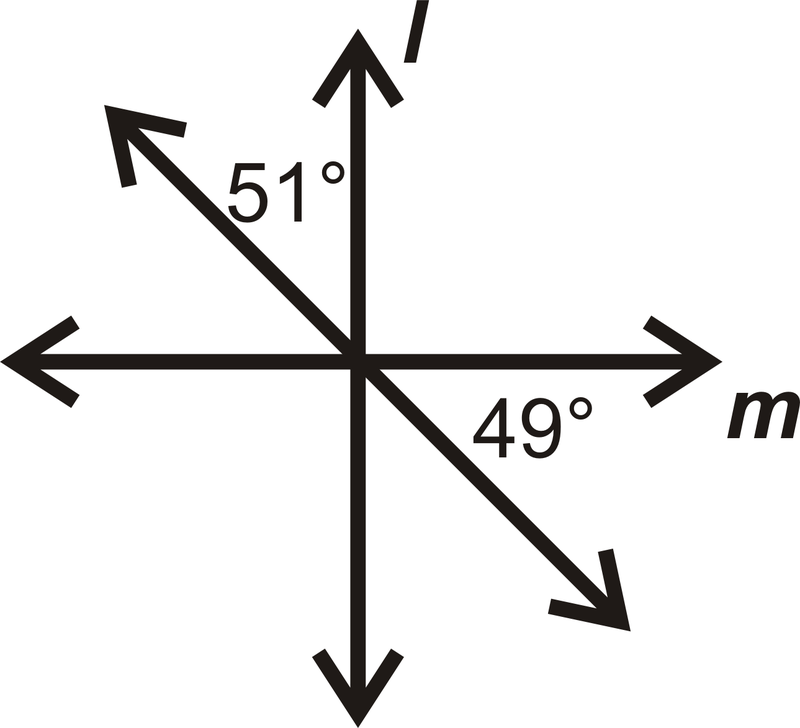
Figura\(\PageIndex{22}\) -
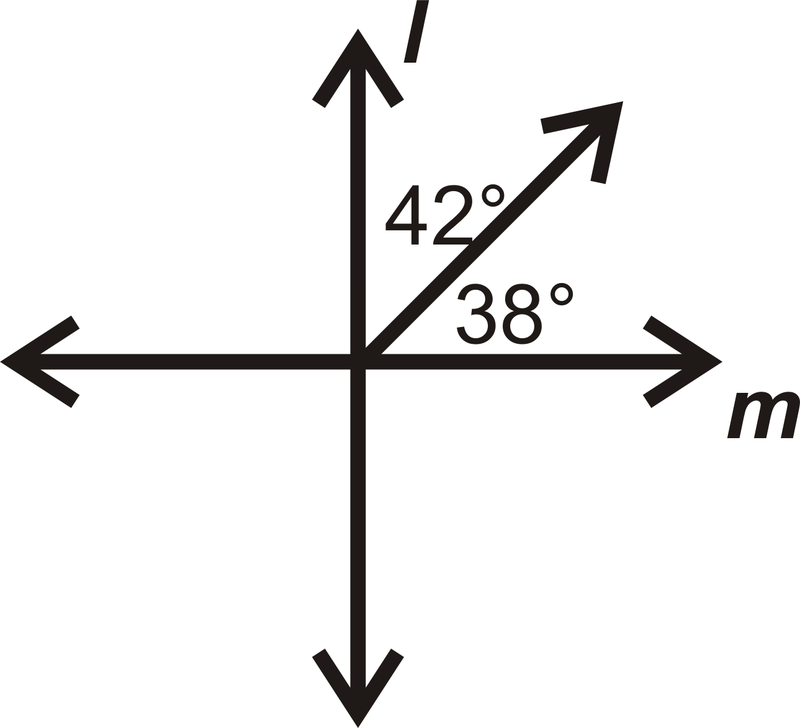
Figura\(\PageIndex{23}\) -
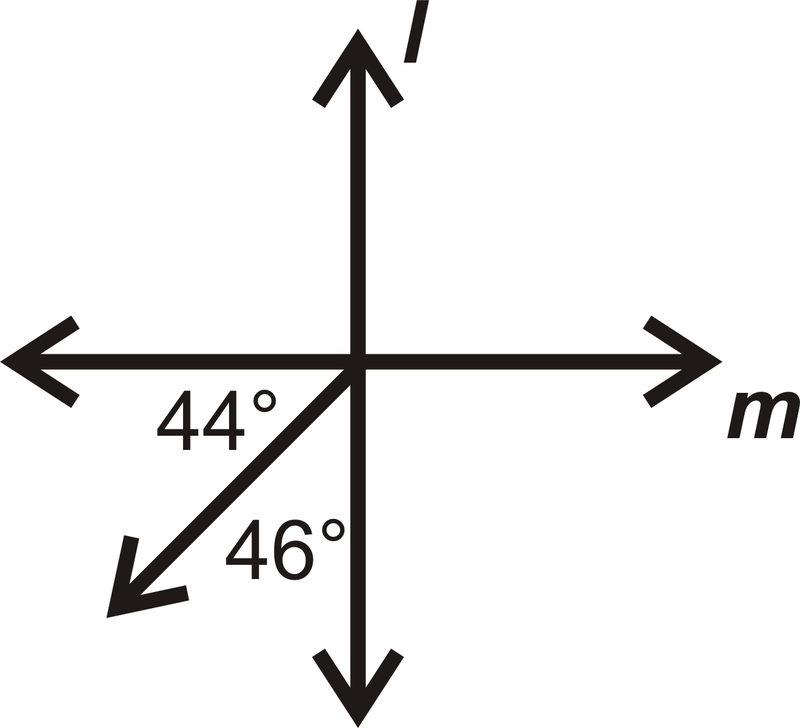
Figura\(\PageIndex{24}\)
Rellene los espacios en blanco en el comprobante a continuación.
- Dado:\(l\perp m\),\(l\perp n\) Demostrar:\(m\parallel n\)
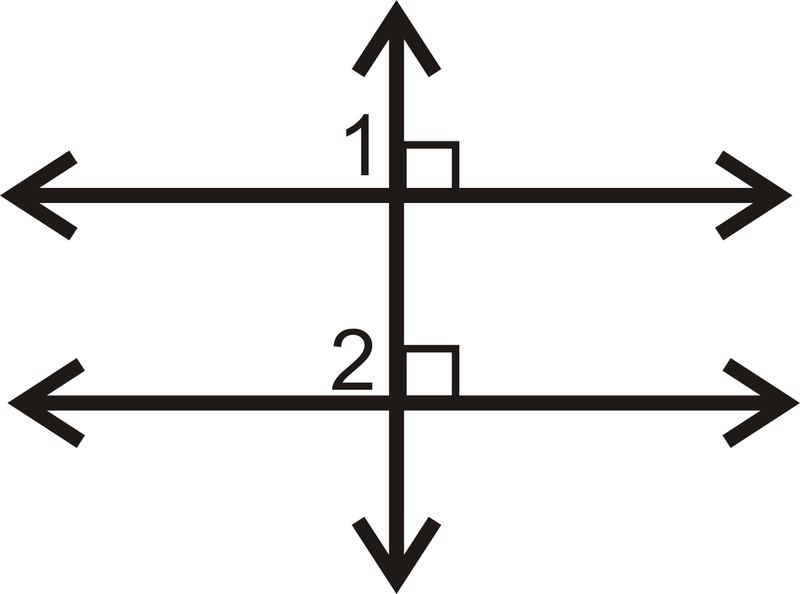
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(\angle 1\)y\(\angle 2\) son ángulos rectos | 2. |
| 3. | 3. Definición de ángulos rectos |
| 4. | 4. Transitivo\(PoE\) |
| 5. \(m\parallel n\) | 5. |
Recursos
El vocabulario
| Término | Definición |
|---|---|
| perpendicular | Dos líneas son perpendiculares cuando se cruzan para formar un\(90^{\circ}\) ángulo. |
| Ángulo | Una figura geométrica formada por dos rayos que conectan en un solo punto o vértice. |
| Líneas perpendiculares | Las líneas perpendiculares son líneas que se cruzan en\(90^{\circ}\) ángulo. |
Recursos adicionales
Elemento Interactivo
Video: Principios de líneas perpendiculares - Básicos
Actividades: Preguntas de discusión de líneas perpendiculares
Ayudas de estudio: Guía de estudio de líneas y ángulos
Práctica: Ángulos y líneas perpendiculares
Mundo real: dando vuelta a las toreras