3.7: Ángulos interiores del mismo lado
- Page ID
- 107372
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ángulos en el mismo lado de una transversal y dentro de las líneas se cruza.
Los ángulos interiores del mismo lado son dos ángulos que están en el mismo lado de la transversal y en el interior de (entre) las dos líneas.
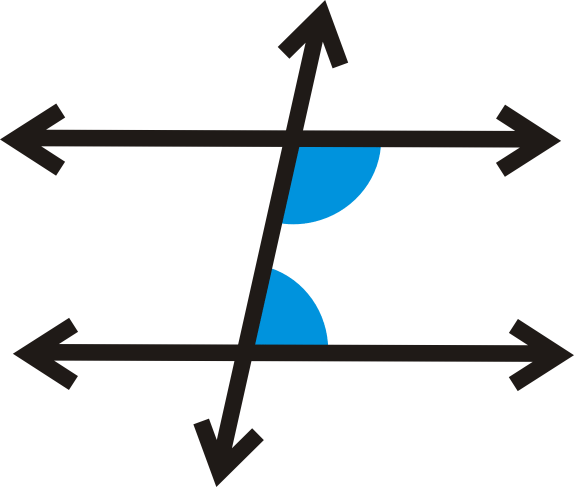
Teorema de ángulos interiores del mismo lado: Si dos líneas paralelas son cortadas por una transversal, entonces los mismos ángulos interiores laterales son suplementarios.
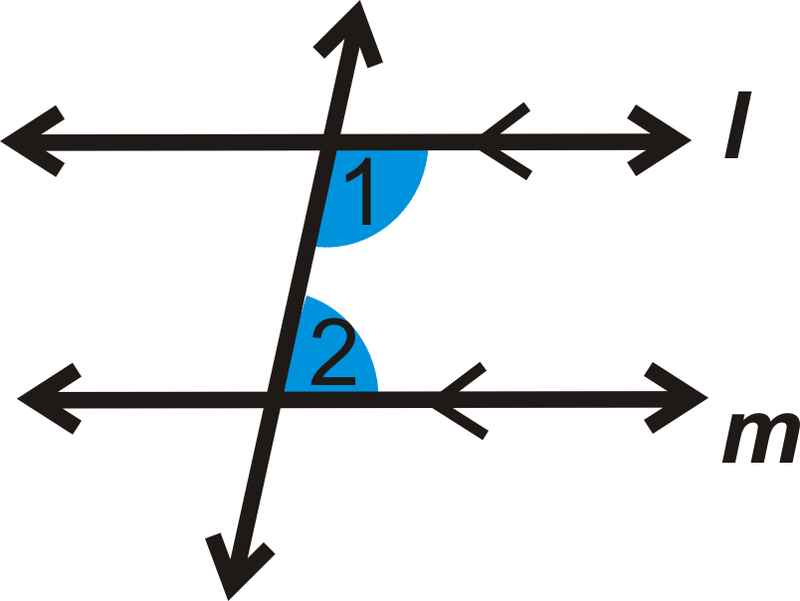
Si\(l \parallel m\), entonces\(m\angle 1+m\angle 2=180^{\circ}\).
Converse del teorema de los ángulos interiores del mismo lado: Si dos líneas son cortadas por una transversal y los ángulos interiores del mismo lado son suplementarios, entonces las líneas son paralelas.
Si
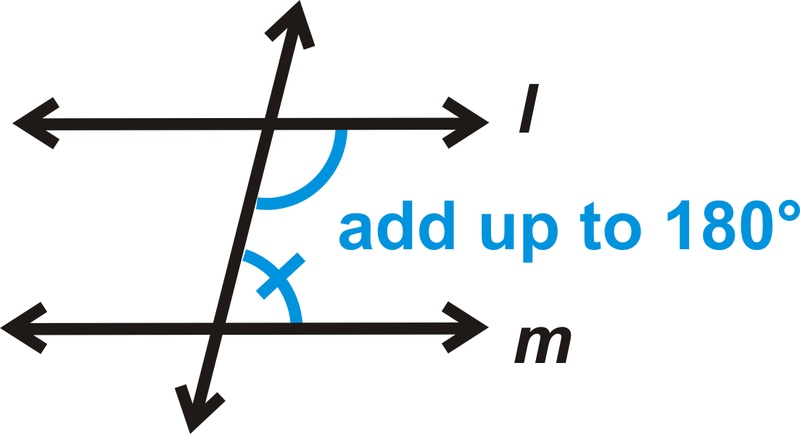
entonces\(l \parallel m\)
Supongamos que se le presentaron dos ángulos que están en el mismo lado de una transversal y entre las dos líneas paralelas cruzadas por la transversal. ¿Cómo describirías estos ángulos y qué podrías concluir sobre sus medidas?
Ejemplo\(\PageIndex{1}\)
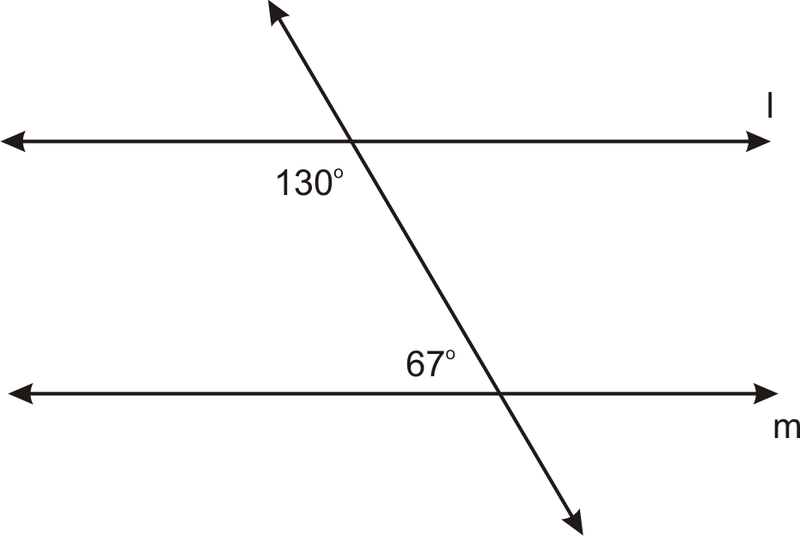
¿Es\(l \parallel m\)? ¿Cómo lo sabes?
Solución
Estos ángulos son ángulos interiores del mismo lado. Entonces, si suman a\(180^{\circ}\), entonces\(l\parallel m\).
\(130^{\circ}+67^{\circ}=197^{\circ}\), por lo tanto las líneas no son paralelas.
Ejemplo\(\PageIndex{2}\)
Dé dos ejemplos de ángulos interiores del mismo lado en el diagrama:
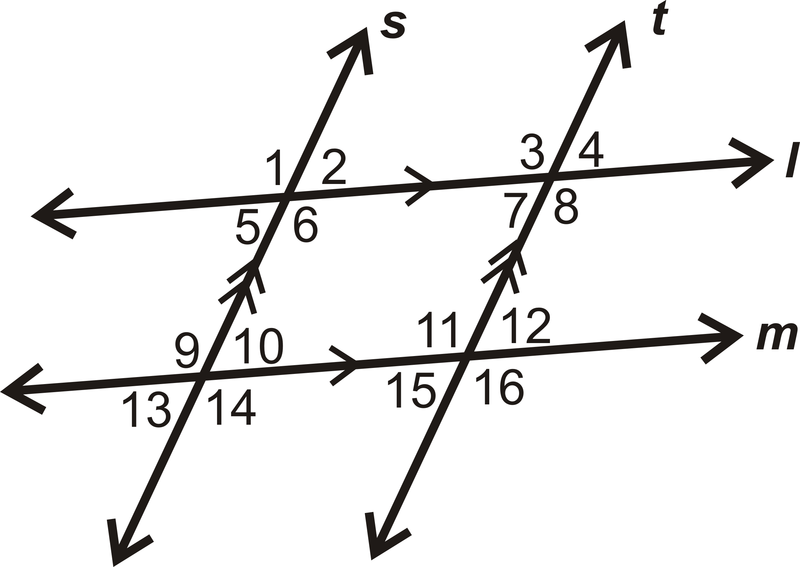
Solución
Hay MUCHOS ejemplos de ángulos interiores del mismo lado en el diagrama. Dos son\(\angle 6\) y\(\angle 10\), y\(\angle 8\) y\(\angle 12\).
Ejemplo\(\PageIndex{3}\)
Encuentra el valor de\(x\).
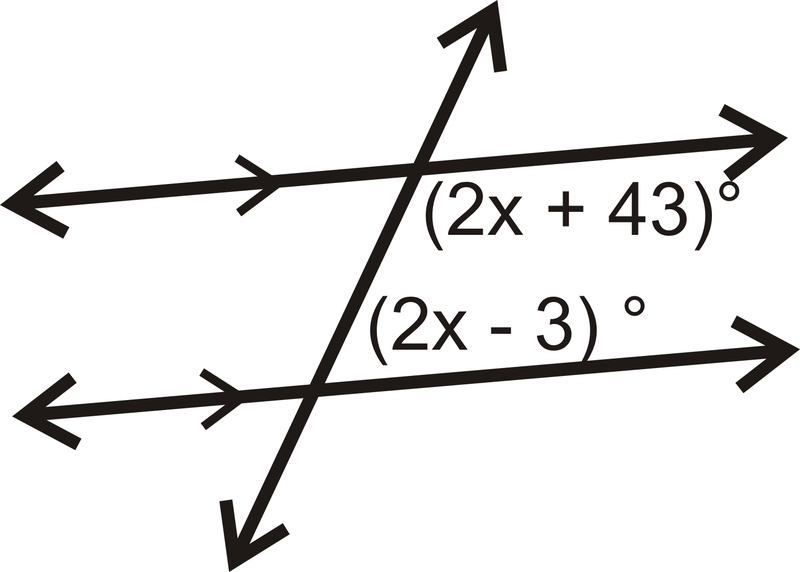
Solución
Los ángulos dados son los mismos ángulos interiores laterales. Debido a que las líneas son paralelas, los ángulos se suman\(180^{\circ}\).
\(\begin{align*}(2x+43)^{\circ}+(2x−3)^{\circ} &=180^{\circ} \\ (4x+40)^{\circ} &=180^{\circ} \\ 4x &=140 \\ x &=35\end{align*}\)
Ejemplo\(\PageIndex{4}\)
Encuentra el valor de\(y\).
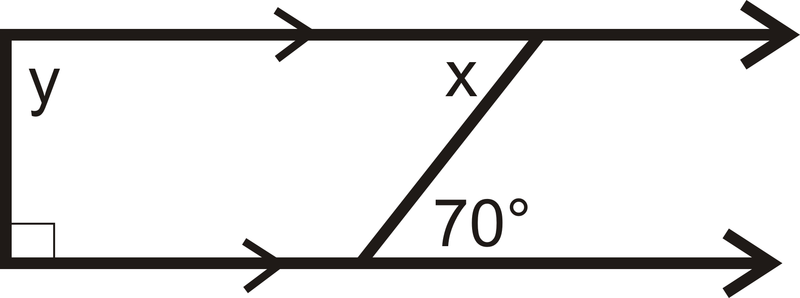Figura\(\PageIndex{7}\)Solución
\(y\)es un mismo ángulo interior lateral con el ángulo recto marcado. Esto significa que\(90^{\circ}+y=180\) así\(y=90\).
Ejemplo\(\PageIndex{5}\)
Encuentra el valor de\(x\) si\(m\angle 3=(3x+12)^{\circ}\) y\(m\angle 5=(5x+8)^{\circ}\).
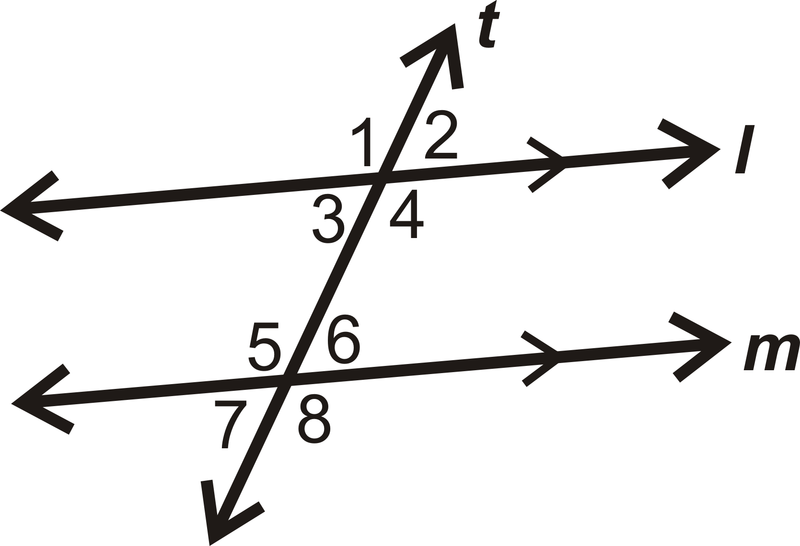
Solución
Estos son los mismos ángulos interiores laterales, así que establece una ecuación y resuelve para\(x\). Recuerda que los mismos ángulos interiores laterales se suman\(180^{\circ}\).
\(\begin{align*} (3x+12)^{\circ}+(5x+8)^{\circ} &=180^{\circ} \\(8x+20)^{\circ} &=180^{\circ} \\8x &=160 \\ x &=20 \end{align*}\)
Revisar
Para las preguntas 1-2, utilice el diagrama para determinar si cada par angular es congruente, suplementario o ninguno.
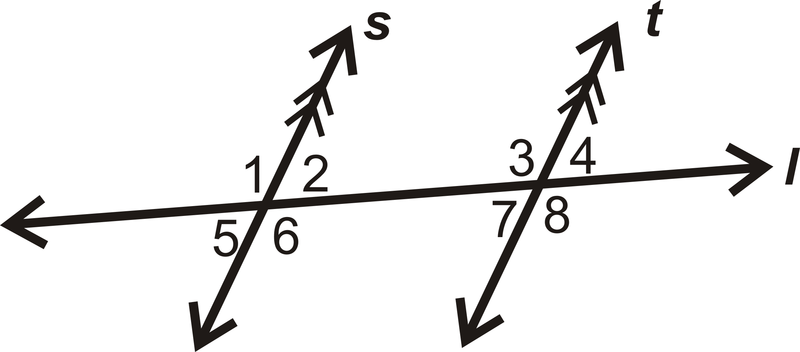
- \(\angle 5\)y\(\angle 8\)
- \(\angle 2\)y\(\angle 3\)
- ¿Las líneas son paralelas? Justifica tu respuesta.
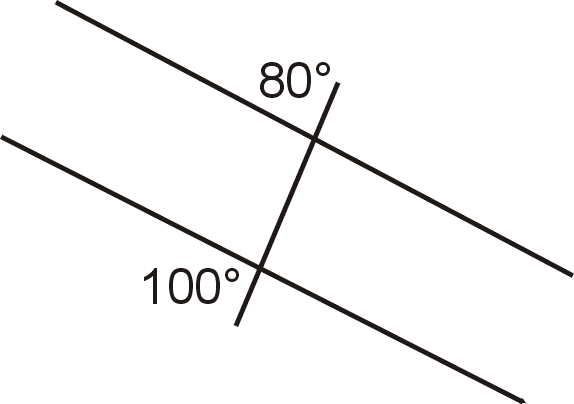
Figura\(\PageIndex{10}\)
En 4-5, use la información dada para determinar qué líneas son paralelas. Si no hay ninguno, escriba ninguno. Considera cada pregunta de manera individual.
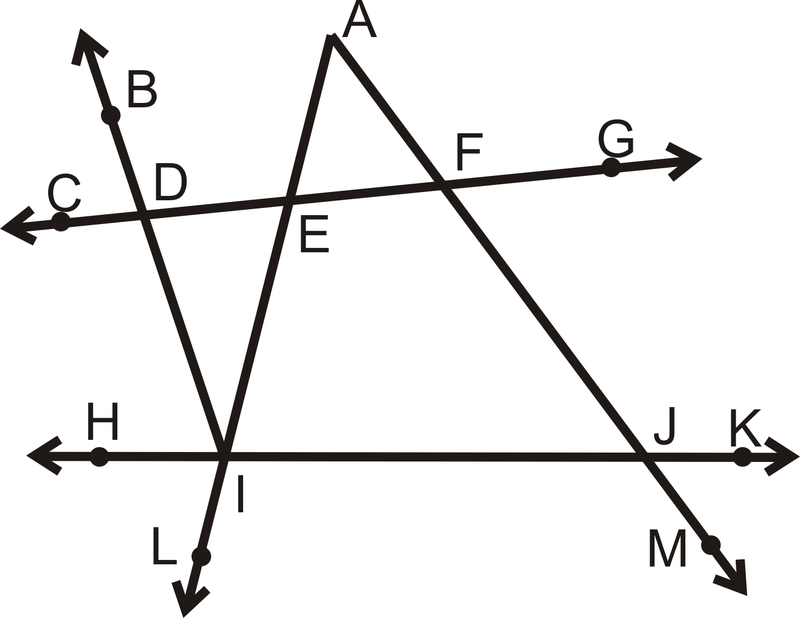
- \(\angle AFD\)y\(\angle BDF\) son complementarios
- \(\angle DIJ\)y\(\angle FJI\) son complementarios
Para 6-8, ¿cuál tiene\(x\) que ser el valor de para hacer paralelas las líneas?
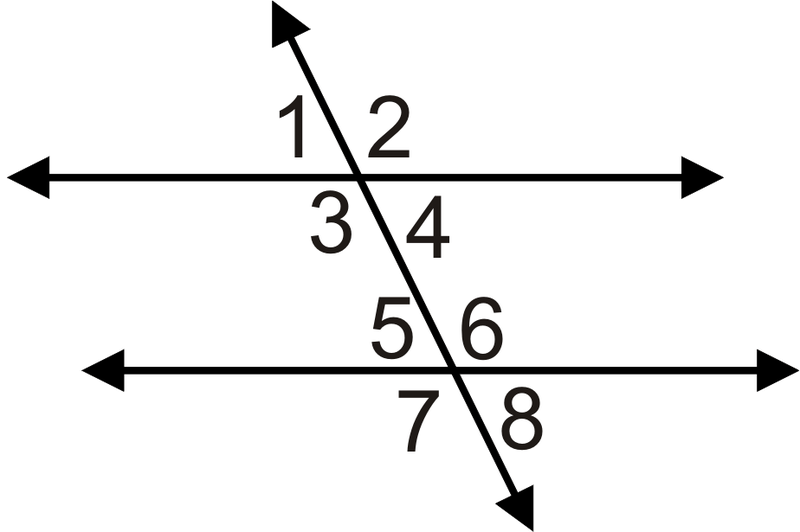
- \(m\angle 3=(3x+25)^{\circ}\)y\(m\angle 5=(4x−55)^{\circ}\)
- \(m\angle 4=(2x+15)^{\circ}\)y\(m\angle 6=(3x−5)^{\circ}\)
- \(m\angle 3=(x+17)^{\circ}\)y\(m\angle 5=(3x−5)^{\circ}\)
Para 9-10, determinar si la afirmación es verdadera o falsa.
- Los ángulos interiores del mismo lado están en el mismo lado de la transversal.
- Los ángulos interiores del mismo lado son congruentes cuando las líneas son paralelas.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.6.
vocabulario
| Término | Definición |
|---|---|
| ángulos interiores del mismo lado | Los ángulos interiores del mismo lado son dos ángulos que están en el mismo lado de la transversal y en el interior de las dos líneas. |
| ángulos suplementarios | Dos ángulos que suman\(180^{\circ}\). |
| transversal | Una línea que cruza otras dos líneas. |
Recurso Adicional
Elemento Interactivo
Video: Principios de ángulos interiores del mismo lado - Básico
Actividades: Preguntas de discusión sobre ángulos interiores del mismo lado
Ayudas de estudio: Guía de estudio de ángulos y transversales
Práctica: Ángulos interiores del mismo lado
Mundo real: ángulos exteriores alternos