3.11: Construcción de Línea
- Page ID
- 107387
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cree líneas que no se crucen ni se crucen en un ángulo de 90 grados usando una brújula y una recta.
Líneas paralelas y perpendiculares
Las construcciones son procesos paso a paso que se utilizan para crear figuras geométricas precisas. Para crear una construcción a mano, hay algunas herramientas que puedes usar:
- Brújula: Un dispositivo que permite crear un círculo con un radio dado. No sólo las brújulas pueden ayudarte a crear círculos, sino que también te pueden ayudar a copiar distancias.
- Enderezado: Cualquier cosa que le permita producir una línea recta. Una recta no debe ser capaz de medir distancias. Una tarjeta de índice funciona bien como una recta. También puedes usar una regla como regla recta, siempre y cuando solo la uses para dibujar líneas rectas y no para medir.
- Papel: Cuando una figura geométrica está sobre una hoja de papel, el papel mismo se puede plegar para construir nuevas líneas.
Para construir líneas paralelas, recuerde que si los ángulos correspondientes son congruentes entonces las líneas son paralelas. Esto significa que si puedes copiar un ángulo para crear ángulos correspondientes congruentes, puedes crear líneas paralelas. Esto se explorará en el Ejemplo A.
Para construir líneas perpendiculares, recuerde que ya sabe construir una bisectriz perpendicular. Puede utilizar este método para construir una línea perpendicular a otra línea a través de cualquier punto dado.
Echemos un vistazo a un problema de ejemplo.
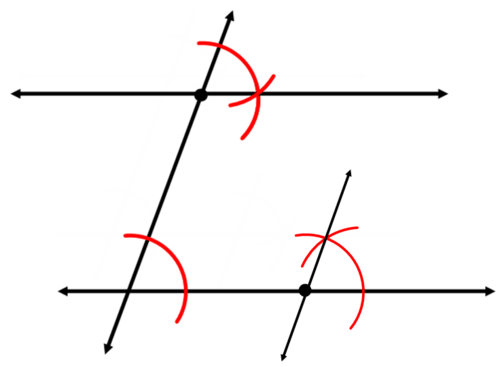
Usa tu recta para dibujar una línea y un punto como el de abajo. Después, construya una línea a través del punto que sea paralela a la línea original.
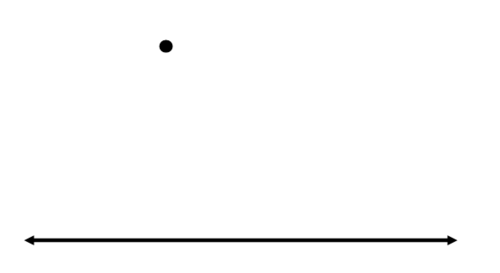
Comience usando su recta para dibujar una línea a través del punto que intersecta la línea original. Esto se convertirá en el transversal después de haber construido la línea paralela.
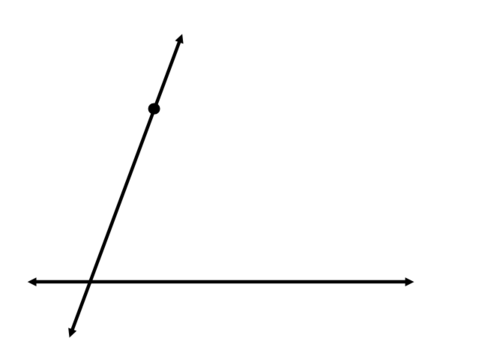
Ahora, tu objetivo es copiar uno de los cuatro ángulos creados en la intersección de las dos líneas. Dibuja un arco a través del ángulo que copiarás:
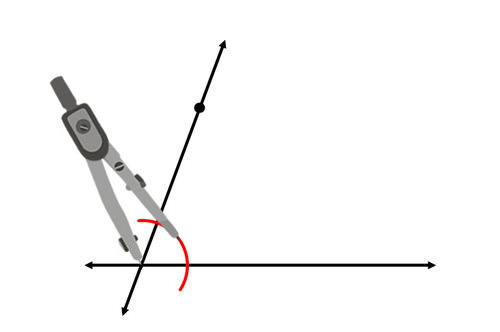
Dibuja un arco con el mismo radio en la ubicación correspondiente, con el punto original como vértice.
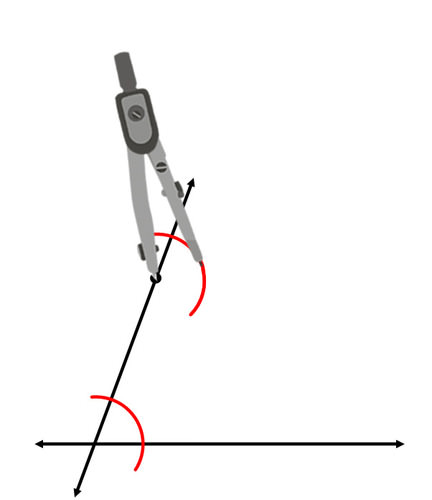
Continúe copiando el ángulo midiendo su ancho y marcando el ancho correcto para el nuevo ángulo.
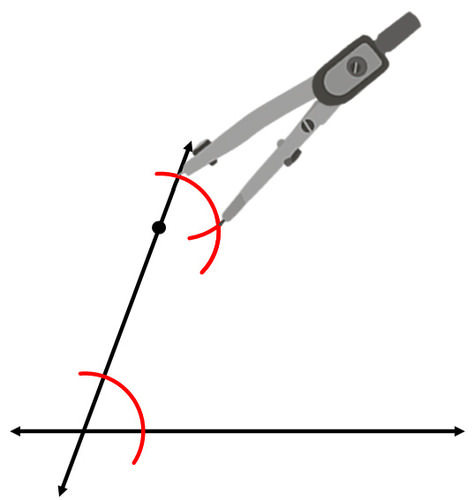
Usa tu recta para construir la línea paralela.
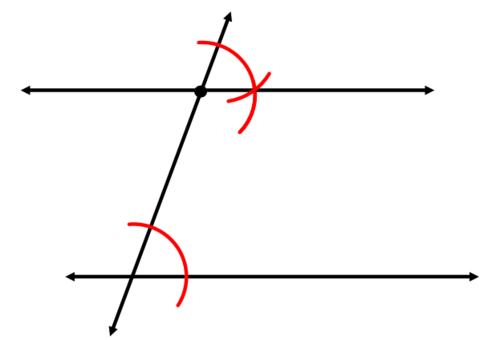
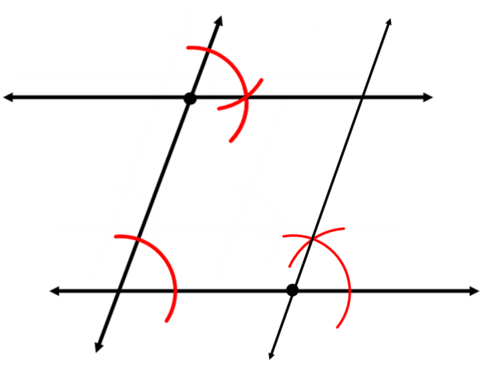
Ahora, vamos a explicar por qué las dos líneas del segundo ejemplo anterior son paralelas.
Si los ángulos correspondientes son congruentes, entonces las líneas son paralelas. En el segundo ejemplo anterior, se copió un ángulo. Esto creó ángulos congruentes. Debido a que el ángulo copiado se puso en la ubicación del ángulo correspondiente, la construcción creó ángulos correspondientes congruentes. Por lo tanto, las dos líneas deben ser paralelas.
Usa tu recta para dibujar una línea y un punto como el de abajo. Después, construya una línea a través del punto que sea perpendicular a la línea original.

Ya sabes cómo construir la bisectriz perpendicular de un segmento. Primero, encuentra un segmento cuya bisectriz perpendicular pasará por el punto dado. Dibuja un círculo parcial centrado en el punto que pasa por la línea dada dos veces.
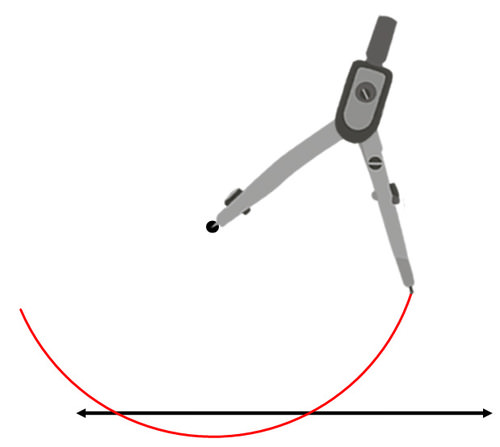
El segmento que conecta los dos puntos de intersección es el segmento para el que construirás una bisectriz perpendicular:
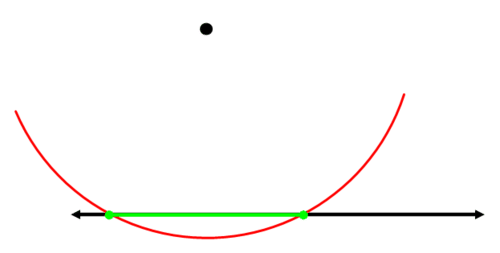
Construye la bisectriz perpendicular del segmento verde:
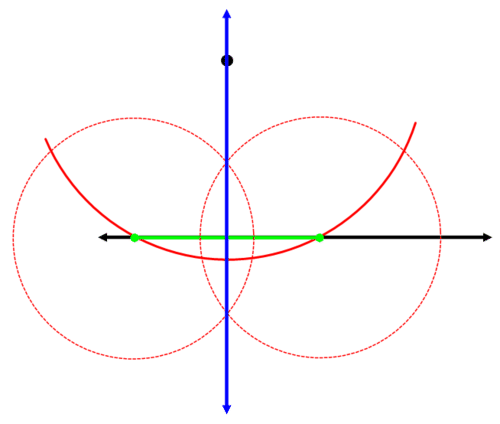
La línea azul es perpendicular a la línea original y pasa por el punto original.
Ejemplo\(\PageIndex{1}\)
Construye un triángulo usando una recta. Ahora construye las tres altitudes del triángulo para encontrar el ortócentro del triángulo.
Solución
Comience con un triángulo genérico:
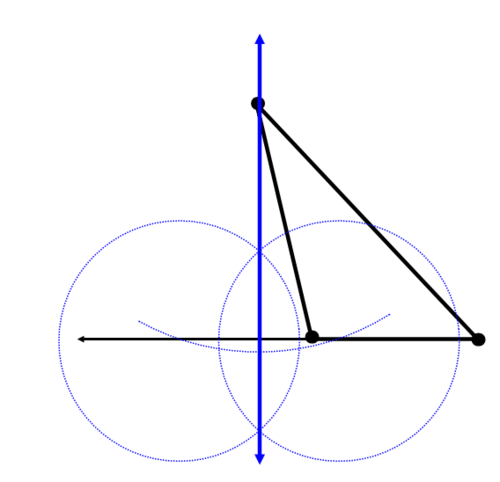
Construye una línea perpendicular a través de cada lado que pase por el vértice opuesto. Podría ser necesario extender la longitud de algunos de los lados. La línea azul de abajo es la primera altitud:
La línea roja es la segunda altitud:
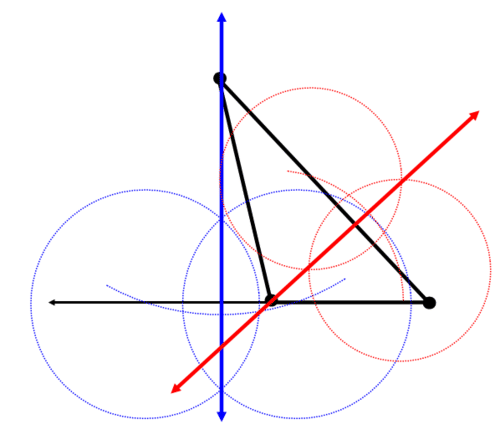
La línea verde es la tercera altitud:
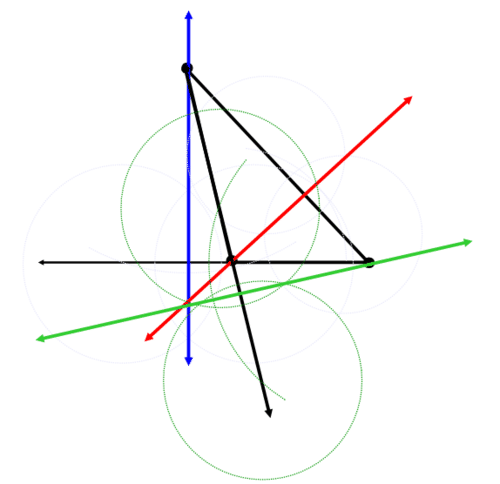
Las líneas azul, roja y verde se cruzan en un punto. Este punto es el ortocentro.
Ejemplo\(\PageIndex{2}\)
Dibuja un segmento de línea. Construya una línea paralela al segmento de línea.
Solución

Ejemplo\(\PageIndex{3}\)
Extiende tu construcción del Ejemplo 2 para construir un paralelogramo.
Solución
Extiende tu construcción del Ejemplo 2 para construir un paralelogramo.
Extender la nueva línea paralela. El cuadrilátero formado es un paralelogramo.
Ejemplo\(\PageIndex{4}\)
¿Cómo puedes estar seguro de que tu cuadrilátero del Ejemplo 3 es un paralelogramo?
Solución
Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. La construcción creó dos pares de líneas paralelas, por lo que el cuadrilátero debe ser un paralelogramo.
Revisar
Dibuja un segmento de línea y un punto.
1. Construya una línea perpendicular al segmento de línea que pasa por el punto.
2. Construya una línea paralela al segmento de línea que pasa por el punto.
3. Extiende tu construcción para construir un rectángulo. Explica lo que hiciste para construir el rectángulo.
Dibuja otro segmento y punto de línea.
4. Construya una línea paralela al segmento de línea que pasa por el punto.
5. Amplíe su construcción para construir un paralelogramo. Explica lo que hiciste para construir el paralelogramo.
Usa una recta para dibujar un triángulo.
6. Construir las altitudes del triángulo.
7. Encuentra el punto de intersección de las altitudes. ¿Qué punto es este?
8. ¿Tu punto de intersección estaba dentro o fuera del triángulo? Si estaba dentro, cree un nuevo triángulo que provoque que el punto de intersección esté fuera del triángulo. Si estaba afuera, cree un nuevo triángulo que provoque que el punto de intersección esté dentro del triángulo.
Dibuja otro segmento y punto de línea.
9. Construya una línea paralela al segmento de línea que pasa por el punto.
10. Extiende tu construcción para construir un trapecio. Explica lo que hiciste para construir el trapecio.
Dibuja otro segmento y punto de línea.
11. Construya una línea perpendicular al segmento de línea que pasa por el punto.
12. Extiende tu construcción para construir un cuadrado. Explica lo que hiciste para construir la plaza.
13. Justifica por qué la forma que creaste en #12 debe ser un cuadrado.
14. Explique por qué el método para construir líneas paralelas implica copiar un ángulo.
15. Explicar por qué el método para construir líneas perpendiculares se basa en el método para construir una bisectriz perpendicular.
vocabulario
| Término | Definición |
|---|---|
| altitud | Una altitud de un triángulo es un segmento de línea desde un vértice y es perpendicular al lado opuesto. También se le llama la altura de un triángulo. |
| Ángulos correspondientes | Los ángulos correspondientes son dos ángulos que están en la misma posición con respecto a la transversal, pero en líneas diferentes. |
| Líneas perpendiculares | Las líneas perpendiculares son líneas que se cruzan en un ángulo de 90°. |
| Vertex | Un vértice es un punto de intersección de las líneas o rayos que forman un ángulo. |
| Ortócentro | El ortocentro es el punto en el que se encuentran las tres altitudes de un triángulo. |

