Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

6.18: Líneas tangentes

Última actualización

30 oct 2022
Guardar como PDF
- 6.17: Ángulos fuera de un círculo
- 6.19: Teorema de las Secantes Intersecantes

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Líneas perpendiculares al radio dibujado al punto de tangencia.

Teoremas de Línea Tangente

Hay dos teoremas importantes sobre las líneas tangentes.

1. Tangente a un teorema de círculo: Una línea es tangente a un círculo si y solo si la línea es perpendicular al radio dibujado al punto de tangencia.

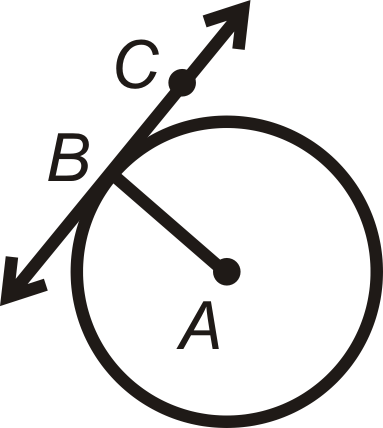
f-d_a0971fc239dff6d9ba0ec252436a0a84dece6826fabe74ed1aa3f444+image_tiny+image_tiny.png — Figura $\PageIndex{1}$

$\overleftrightarrow{BC}$ es tangente en el punto $B$ si y solo si $\overleftrightarrow{BC}\perp \overline{AB}$ .

Este teorema utiliza las palabras “si y solo si”, convirtiéndolo en una declaración bicondicional, lo que significa que lo contrario de este teorema también es cierto.

2. Teorema de dos tangentes: Si se dibujan dos segmentos tangentes a un círculo desde el mismo punto externo, entonces son congruentes.

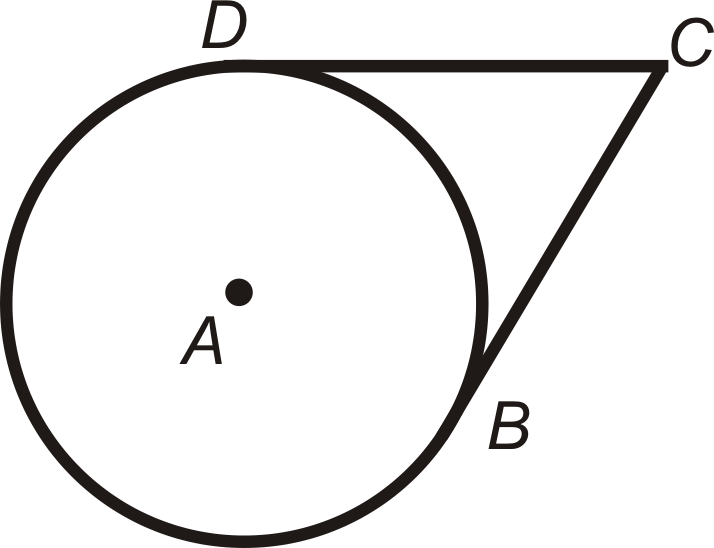
F-D_14fcbbb368146783d10f3f271012b1165e8b2e432d8abc8c291e944c+imagen_tiny+imagen_tiny.png — Figura $\PageIndex{2}$

$\overline{BC}$ y $\overline{DC}$ tienen $C$ como punto final y son tangentes; $\overline{BC}\cong \overline{DC}$ .

¿Y si se dibujara una línea fuera de un círculo que pareciera tocar el círculo en un solo punto? ¿Cómo podrías determinar si esa línea era en realidad una tangente?

Ejemplo $\PageIndex{1}$

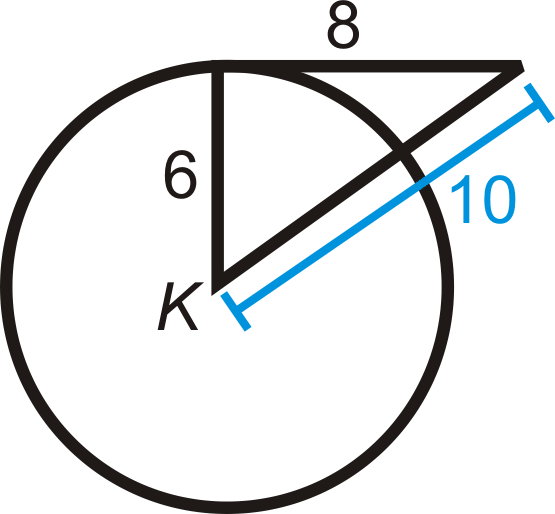
Determina si el triángulo de abajo es un triángulo rectángulo.

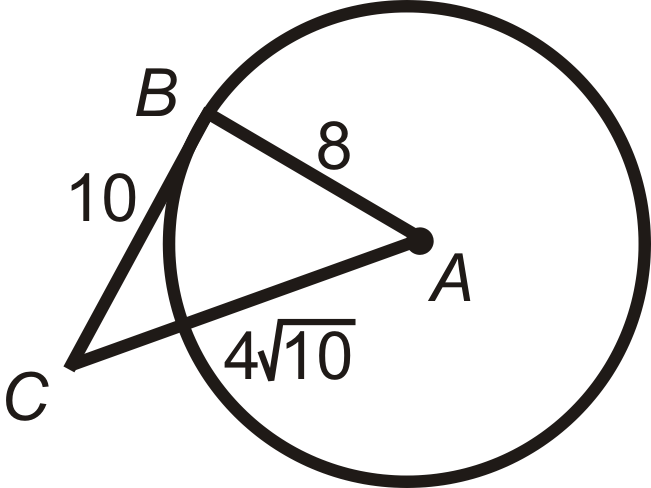
f-d_ce2c0b86512dc266c82c4ac4b7c56edfe31136f8b9ef60bf1172893d+image_tiny+image_tiny.png — Figura $\PageIndex{3}$

Solución

Usa el Teorema de Pitágoras. $4\sqrt{10}$ es el lado más largo, así será $c$ .

Hace

$\begin{aligned} 8^2+10^2&= (4\sqrt{10})^2? \\ 64+100&\neq 160\end{aligned}$

$\Delta ABC$ no es un triángulo rectángulo. A partir de esto, también encontramos que no $\overline{CB}$ es tangente a $\bigodot A$ .

Ejemplo $\PageIndex{2}$

Si $D$ y $C$ son los centros y $AE$ es tangente a ambos círculos, encuentra $DC$ .

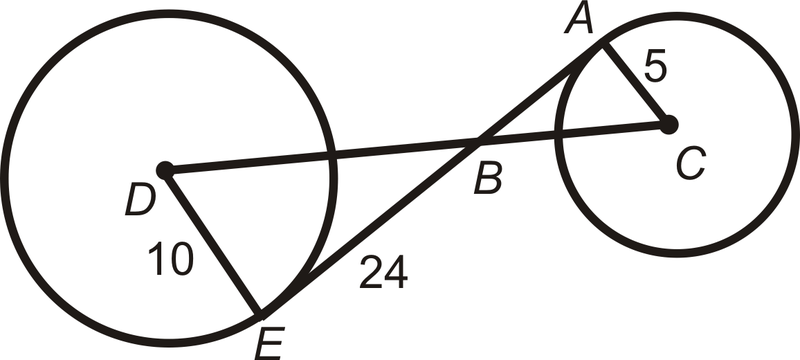
F-d_1617d3b1028c861a04cddc19d995e14943d47798007fad38e0b099a4+image_tiny+image_tiny.png — Figura $\PageIndex{4}$

Solución

$\overline{AE}\perp \overline{DE}$ $\overline{AE}\perp \overline{AC}$ y $\Delta ABC \sim \Delta DBE$ por AA Similaridad.

Para encontrar $DB$ , usa el Teorema de Pitágoras.

$\begin{aligned} 10^2+24^2&=DB^2 \\ 100+576&=676 \\ DB&=\sqrt{676}=26 \end{aligned}$

Para encontrar $BC$ , usa triángulos similares.

$\dfrac{5}{10}=\dfrac{BC}{26}\rightarrow BC=13. \: DC=DB+BC=26+13=39$

Ejemplo $\PageIndex{3}$

$\overline{CB}$ es tangente a $\bigodot A$ en el punto $B$ . Encuentra $AC$ . Reducir cualquier tipo de radicales.

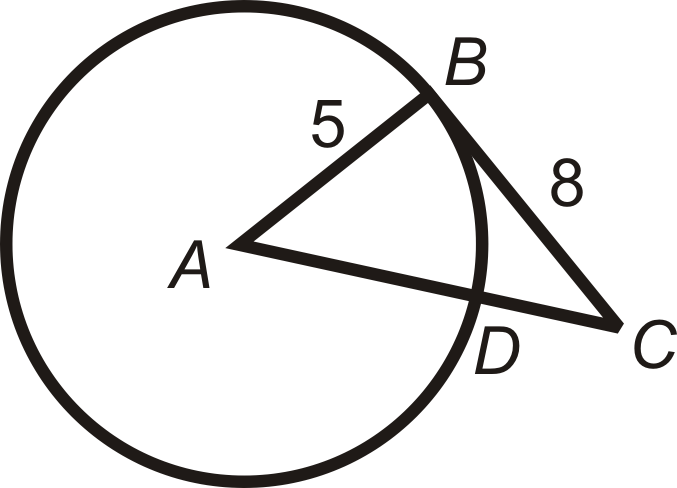
f-d_7db605d5ba0749e9e138a8becd3bfeba5bedd1a4561ccd6355e5c906+image_tiny+imagen_tiny.png — Figura $\PageIndex{5}$

Solución

$\overline{CB}$ es tangente, así $\overline{AB}\perp \overline{CB}$ y $\Delta ABC$ un triángulo rectángulo. Usa el Teorema de Pitágoras para encontrar $AC$ .

$\begin{aligned} 5^2+8^2&=AC^2 \\ 25+64&=AC^2 \\ 89&=AC^2 \\ AC&=\sqrt{89}\end{aligned}$

Ejemplo $\PageIndex{4}$

Usando la respuesta del Ejemplo A anterior, encuentre $DC$ en $\bigodot A$ . Redondee su respuesta a la centésima más cercana.

F-D_99633BA38dbafd08d7442ab8fc5090387b64d0200713ee9645bcbdb5+image_tiny+image_tiny.png — Figura $\PageIndex{6}$

Solución

$\begin{aligned} DC&=AC−AD \\ DC&=\sqrt{89}−5 \approx 4.43 \end{aligned}$

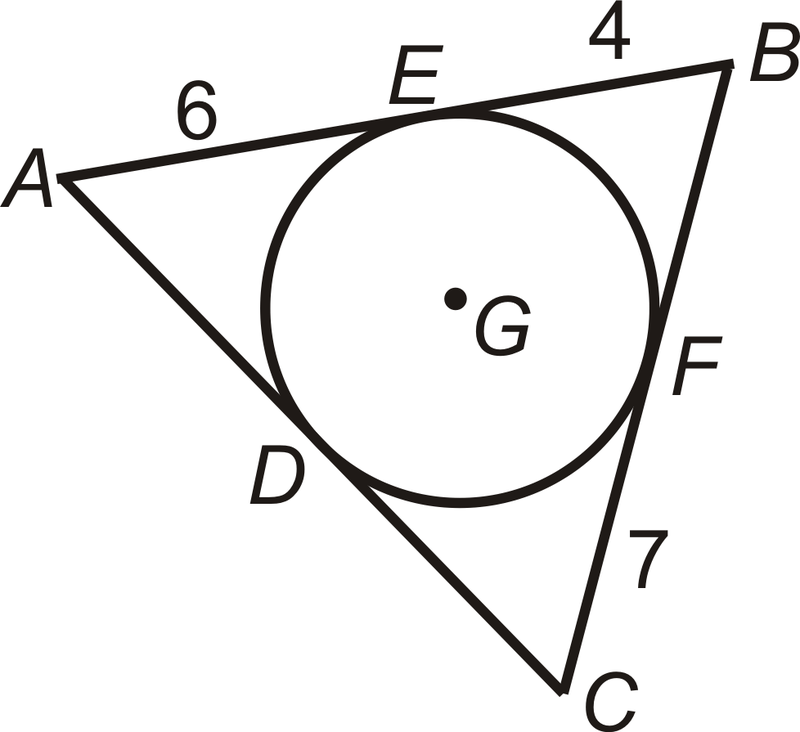
Ejemplo $\PageIndex{5}$

Encuentra el perímetro de $\Delta ABC$ .

f-d_57357abae2dd43ff73b3e6f00306589f2dc9181cef73c05b80c77634+imagen_tiny+imagen_tiny.png — Figura $\PageIndex{7}$

Solución

$AE=AD$ , $EB=BF$ , y $CF=CD$ . Por lo tanto, el perímetro de

$\Delta ABC=6+6+4+4+7+7=34$ .

$\bigodot G$ está inscrito en $\Delta ABC$ . Un círculo se inscribe en un polígono si cada lado del polígono es tangente al círculo.

Revisar

Determinar si el segmento dado es tangente a $\bigodot K$ .

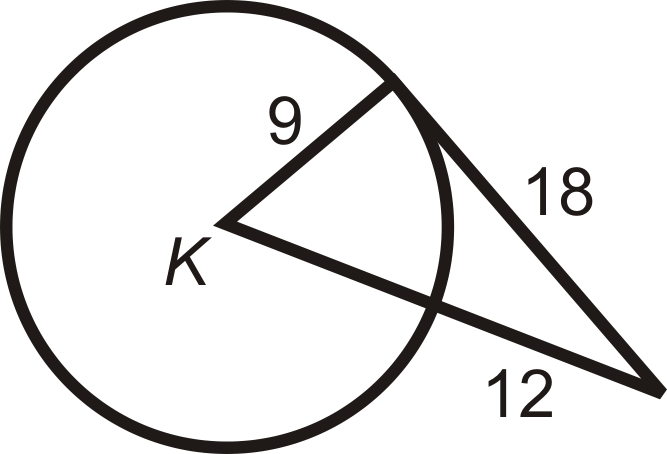
Figura $\PageIndex{8}$
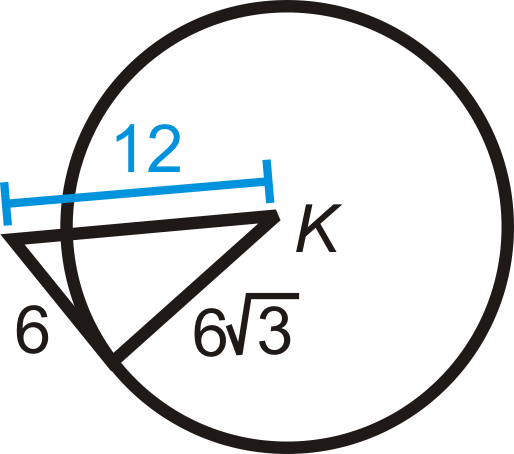
Figura $\PageIndex{9}$
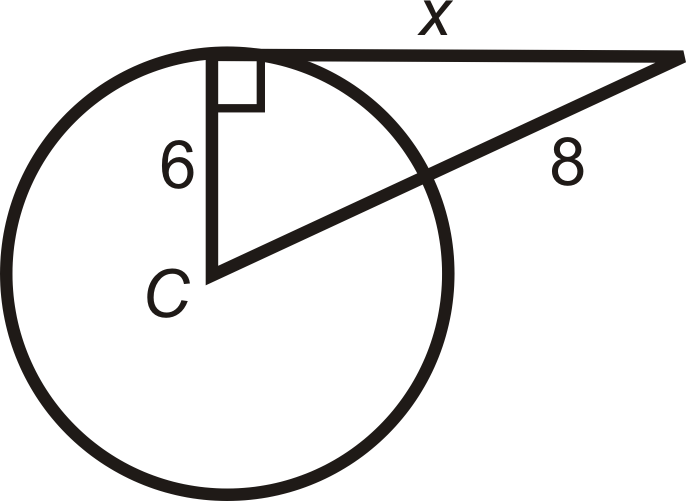
Figura $\PageIndex{10}$

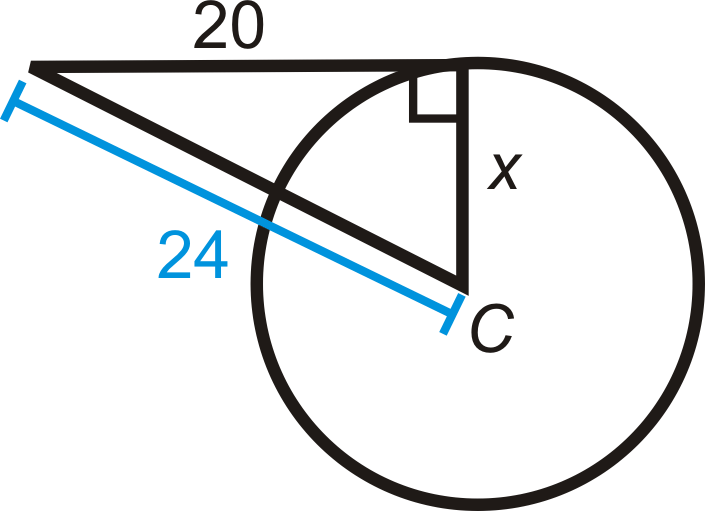
Encuentra el valor de la (s) longitud (s) indicada (s) en $\bigodot C$ . $A$ y $B$ son puntos de tangencia. Simplifica todos los radicales.

Figura $\PageIndex{11}$
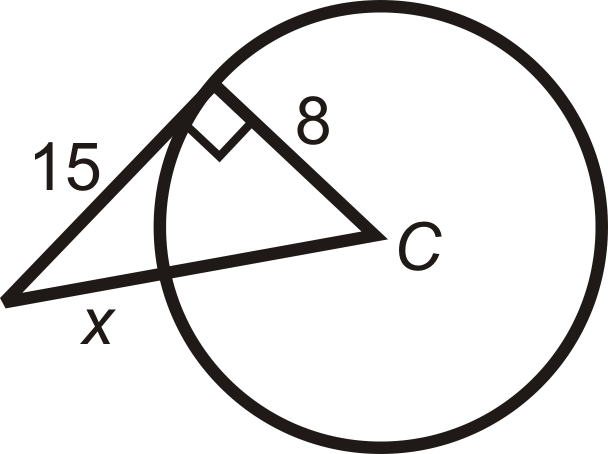
Figura $\PageIndex{12}$
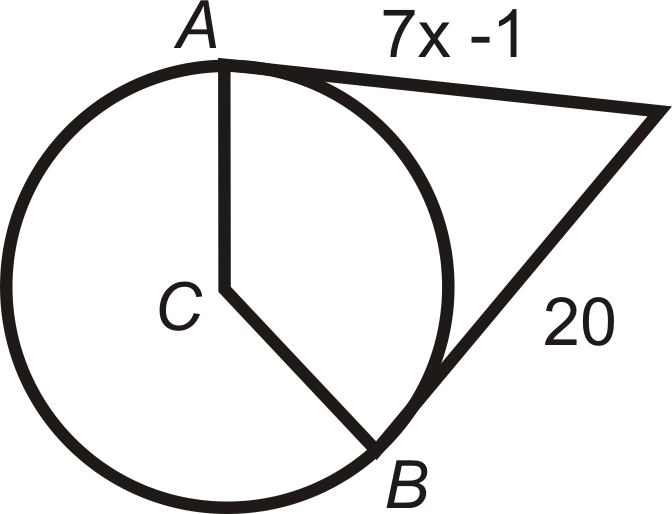
Figura $\PageIndex{13}$
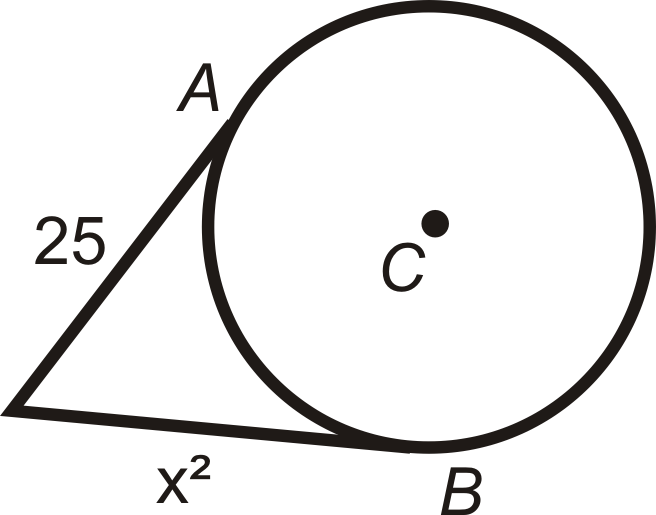
Figura $\PageIndex{14}$
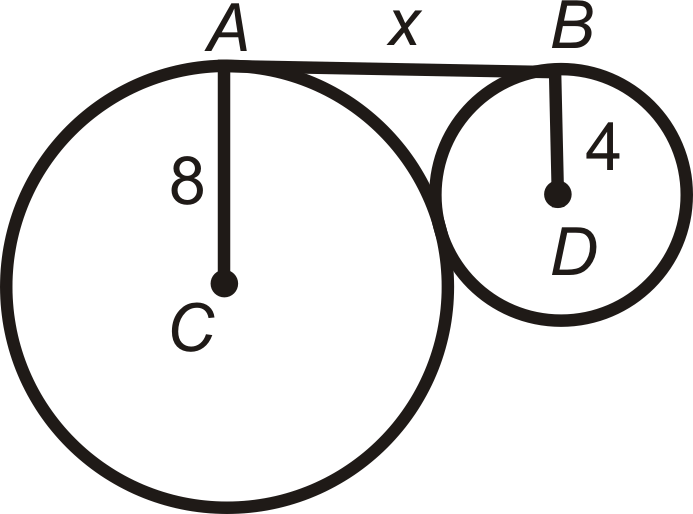
Figura $\PageIndex{15}$
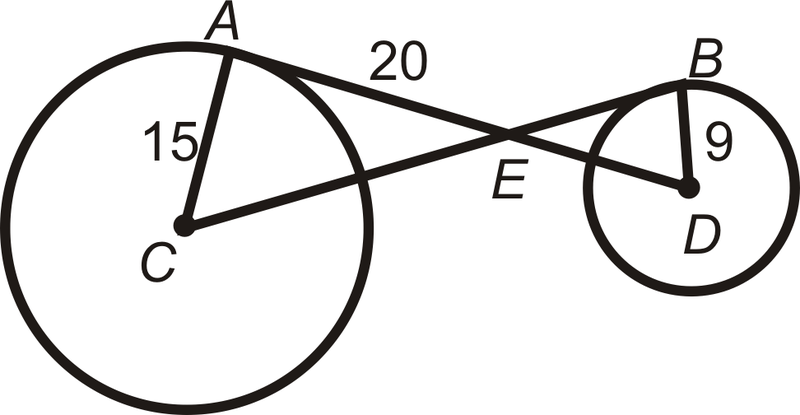
Figura $\PageIndex{16}$

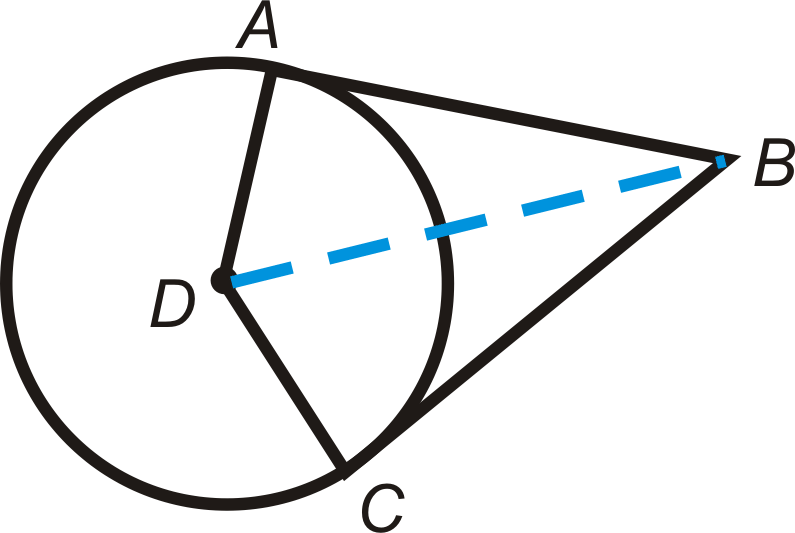
$A$ y $B$ son puntos de tangencia para $\bigodot C$ y $\bigodot D$ .

f-d_8e79fb92c98d8ea0e039782ca211671bc23cc0d7e4a2ca5082e648a9+image_tiny+image_tiny.png — Figura $\PageIndex{17}$

¿Es $\Delta AEC \sim \Delta BED$ ? ¿Por qué?
Encuentra $CE$ .
Encuentra $BE$ .
Encuentra $ED$ .
Encontrar $BC$ y $AD$ .

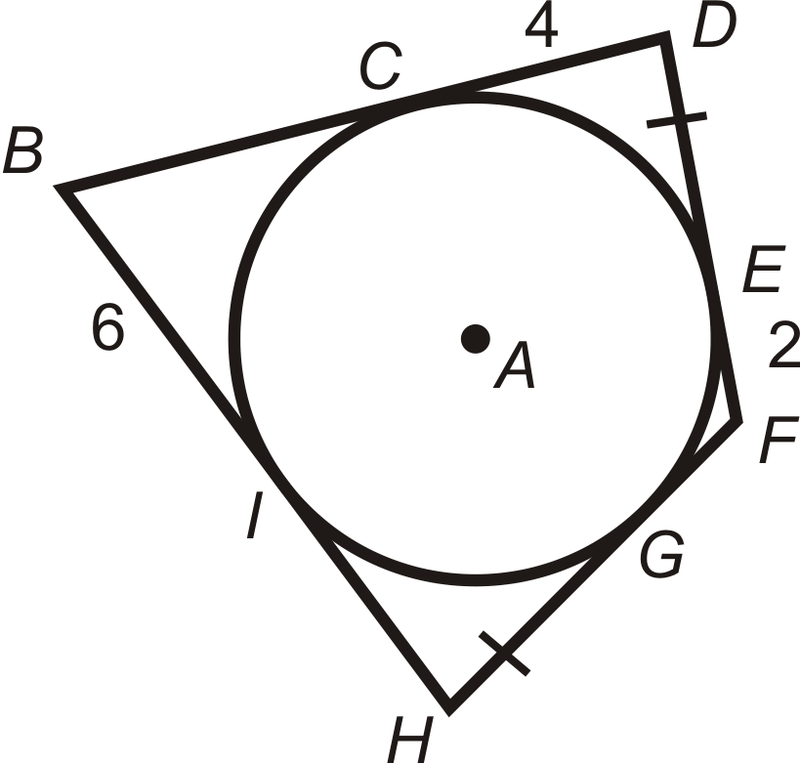
$\bigodot A$ está inscrito en $BDFH$ .

f-d_a5ada34d86ef344bb8edfa9c48aec1f4bb5e3c166f912e1bd96bcc89+image_tiny+image_tiny.png — Figura $\PageIndex{18}$

Encuentra el perímetro de $BDFH$ .
¿Qué tipo de cuadrilátero es $BDFH$ ? ¿Cómo lo sabes?
Dibuja un círculo inscrito en un cuadrado. Si el radio del círculo es 5, ¿cuál es el perímetro de la plaza?
¿Se puede inscribir un círculo en un rectángulo? Si es así, dibuja. Si no, explique.
Dibuja un triángulo con dos lados tangentes a un círculo, pero el tercer lado no lo es.
¿Se puede inscribir un círculo en un triángulo obtuso? Si es así, dibuja. Si no, explique.
Rellene los espacios en blanco en la prueba del Teorema de las Dos Tangentes.

Dado: $\overline{AB}$ y $\overline{CB}$ con puntos de tangencia en $A$ y $C$ . $\overline{AD}$ y $\overline{DC}$ son radios.

Demostrar: $\overline{AB}\cong \overline{CB}$

*Declaración*	*Razón*
1.	1.
2. $\overline{AD}\cong \overline{DC}$	2.
3. $\overline{DA}\perp \overline{AB}$ y $\overline{DC}\perp \overline{CB}$	3.
4.	4. Definición de líneas perpendiculares
5.	5. Conexión de dos puntos existentes
6. $\Delta ADB$ y $\Delta DCB$ son triángulos rectos	6.
7. $\overline{DB}\cong\overline{DB}$	7.
8. $\Delta ABD\cong \Delta CBD$	8.
9. $\overline{AB}\cong \overline{CB}$	9.

Rellene los espacios en blanco, utilizando la prueba de #21.
1. $ABCD$ es un _____________ (tipo de cuadrilátero).
2. La línea que conecta el ___________ y el punto externo $B$ __________ $\angle ABC$ .
Puntos $A$ , $B$ , y $C$ son puntos de tangencia para los tres círculos tangentes. Explique por qué $\overline{AT}\cong \overline{BT}\cong \overline{CT}$ .

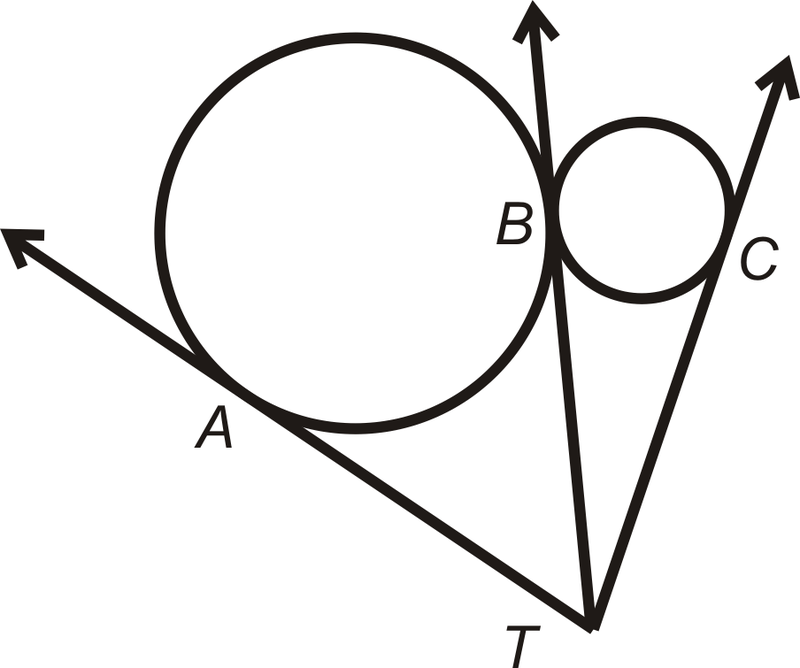
Figura $\PageIndex{19}$

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.2.

Recursos

vocabulario

Término	Definición
círculo	El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el *centro*.
diámetro	Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio.
punto de tangencia	El punto donde la línea tangente toca el círculo.
radio	La distancia desde el centro hasta el borde exterior de un círculo.
Tangente	La tangente de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud del lado adyacente al ángulo dado.
Teorema de la tangente a un círculo	Una línea es tangente a un círculo si y sólo si la línea es perpendicular al radio dibujado al punto de tangencia.
Teorema de dos tangentes	El Teorema de Dos Tangentes establece que si se dibujan dos segmentos tangentes a un círculo desde un mismo punto externo, entonces son congruentes.

Recursos adicionales

Elemento Interactivo

Video: Principios de Líneas Tangentes - Básicos

Actividades: Preguntas de discusión sobre líneas tangentes

Ayudas de estudio: Propiedades de una guía de estudio circular

Práctica: Líneas tangentes

Mundo real: Swing Rides

Teoremas de Línea Tangente

Revisar

Reseña (Respuestas)

Recursos

vocabulario

Recursos adicionales

Support Center

How can we help?