6.16: Ángulos sobre y dentro de un círculo

Ángulos cuyos vértices están en la circunferencia de un círculo o formados por líneas tangentes y acordes.

Cuando decimos que un ángulo está en un círculo, queremos decir que el vértice está en el borde del círculo. Un tipo de ángulo en un círculo es el ángulo inscrito (ver Ángulos Inscritos en Círculos). Otro tipo de ángulo en un círculo es uno formado por una tangente y una cuerda.

Teorema de ángulo de cord/ tangente: La medida de un ángulo formado por una cuerda y una tangente que se cruzan en un círculo es la mitad de la medida del arco interceptado.

Figura\(\PageIndex{1}\)

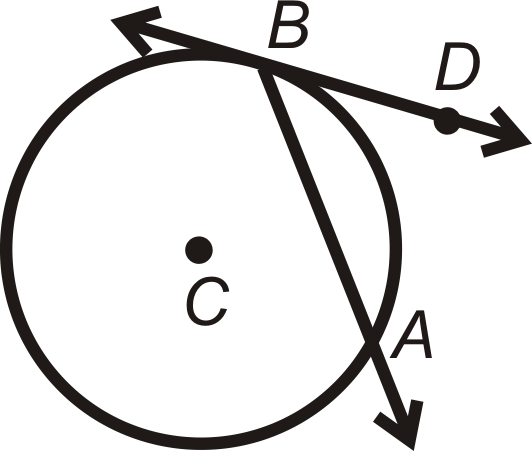
\(m\angle DBA=\dfrac{1}{2}m\widehat{AB}\)

Si dos ángulos, con sus vértices en el círculo, interceptan el mismo arco entonces los ángulos son congruentes.

Un ángulo está dentro de un círculo cuando el vértice se encuentra en cualquier lugar dentro del círculo.

Teorema de ángulo de acordes de intersección: La medida del ángulo formado por dos acordes que se cruzan dentro de un círculo es el promedio de las medidas de los arcos interceptados.

Figura\(\PageIndex{2}\)

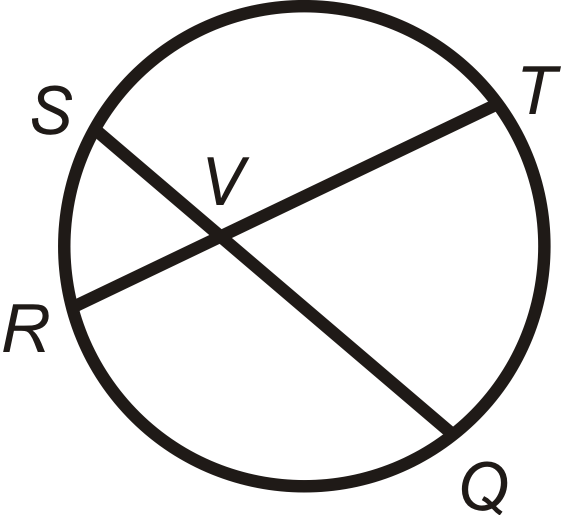
\(\begin{aligned}m\angle SVR&=\dfrac{1}{2}(m\widehat{SR} +m\widehat{TQ} )=m\widehat{SR} +m\widehat{TQ} 2=m\angle TVQ \\ m\angle SVT&=\dfrac{1}{2}(m\widehat{ST} +m\widehat{RQ} )=m\widehat{ST} +m\widehat{RQ} 2=m\angle RVQ\end{aligned}\)

¿Y si te dieran un círculo con un acorde y una tangente o dos acordes que se encuentran en un punto común? ¿Cómo podrías usar la medida del arco (s) formado (s) por esas partes del círculo para encontrar la medida de los ángulos que hacen sobre o dentro del círculo?

Ejemplo\(\PageIndex{1}\)

Encuentra\(x\).

Figura\(\PageIndex{3}\)

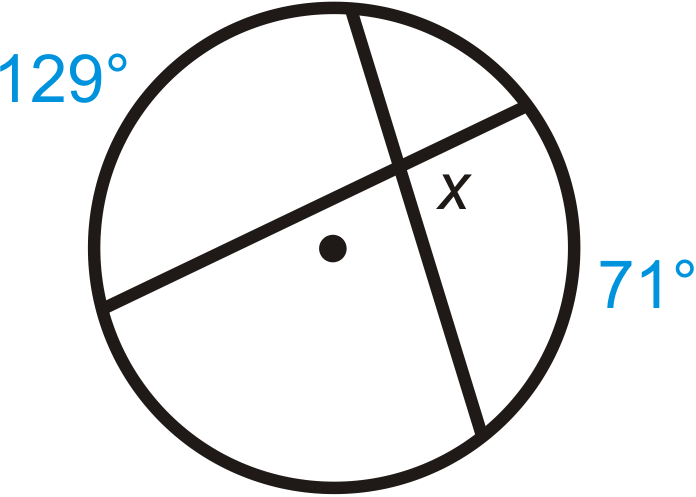
Solución

Utilice el Teorema de Ángulo de Acordes Intersectados para escribir una ecuación.

\(x=\dfrac{129^{\circ}+71^{\circ}}{2}=\dfrac{200^{\circ}}{2}=100^{\circ}\)

Ejemplo\(\PageIndex{2}\)

Encuentra\(x\).

Figura\(\PageIndex{4}\)

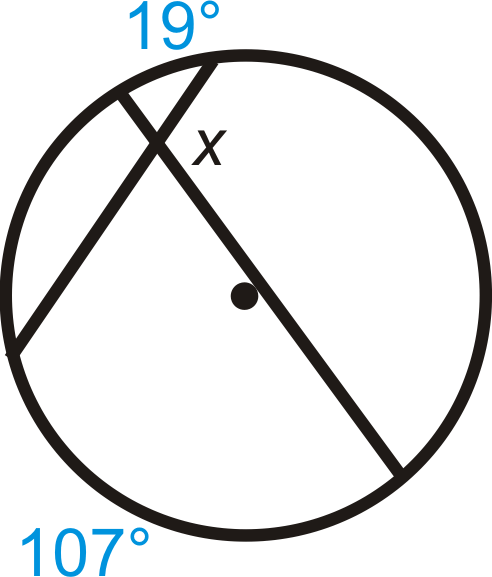
Solución

Utilice el Teorema de Ángulo de Acordes Intersectados para escribir una ecuación.

\(x\)es complementario al ángulo que es el promedio de los arcos interceptados dados. A esto lo llamamos ángulo suplementario\(y\).

\(y=\dfrac{19^{\circ}+107^{\circ}}{2}=\dfrac{126^{\circ}}{2}=63^{\circ} \qquad x+63^{\circ}=180^{\circ}; \: x=117^{\circ}\)

Ejemplo\(\PageIndex{3}\)

Encuentra\(m\angle BAD\).

Figura\(\PageIndex{5}\)

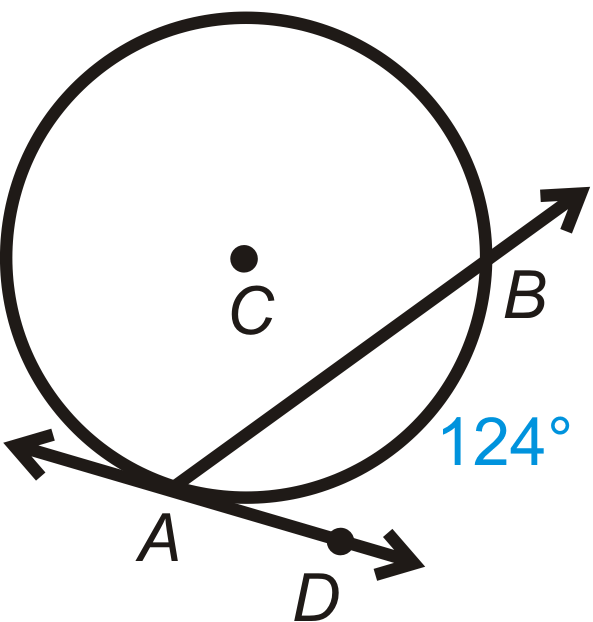
Solución

Usa el Teorema del Ángulo Acorde/Tangente. \(m\angle BAD=\dfrac{1}{2}m\widehat{AB}=\dfrac{1}{2}\cdot 124^{\circ}=62^{\circ}\).

Ejemplo\(\PageIndex{4}\)

Encontrar\(a\),\(b\), y\(c\).

Figura\(\PageIndex{6}\)

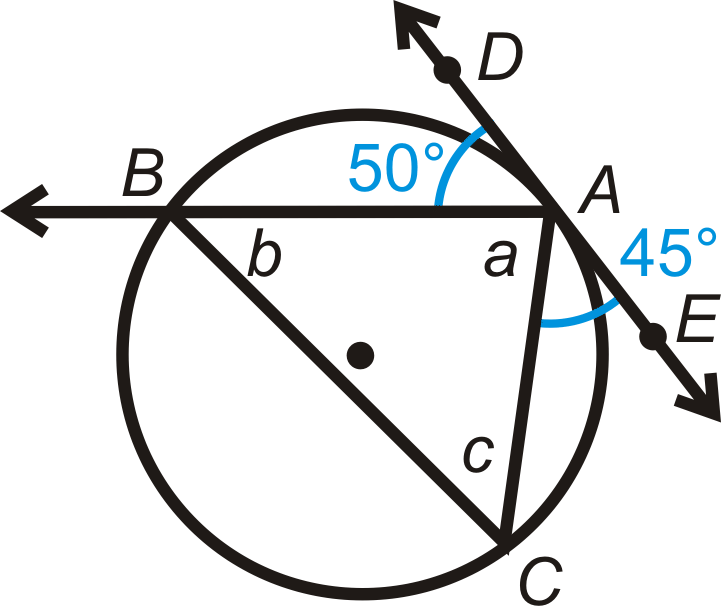
Solución

\ (\ begin {array} {c}
50^ {\ circ} +45^ {\ circ} +m\ ángulo a=180^ {\ circ}\ quad\ text {ángulo recto}\\
m\ ángulo a=85^ {\ circ}\\
m\ ángulo b=\ frac {1} {2}\ cdot m\ sombrero ancho {A C}\
\ qqbegin {array} {c}
\ sombrero ancho {A C} =2\ cdot m\ ángulo E A C=2\ cdot 45^ {\ circ} =90^ {\ circ}\
m\ ángulo b=\ frac {1} {2}\ cdot 90^ {\ circ} =45^ {\ circ}\ end {array}
\\
85^ {\ circ} +45^ {\ circ} +m\ ángulo c=180^ {\ circ} quad\ texto {\ circ} teorema de la suma del triángulo}\\
m\ ángulo c=50^ {\ circ}
\ end {array}\)

Ejemplo\(\PageIndex{5}\)

Encuentra\(m\widehat{AEB}\).

Figura\(\PageIndex{7}\)

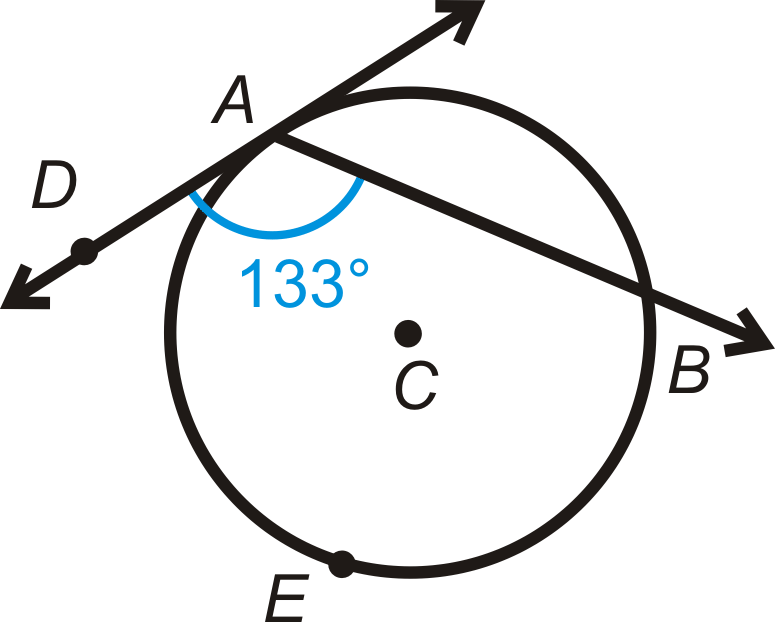
Solución

Usa el Teorema del Ángulo Acorde/Tangente. \(m\widehat{AEB}=2\cdot m\angle DAB=2\cdot 133^{\circ}=266^{\circ}.\)

Revisar

Encuentra el valor de las variables faltantes.

1. 

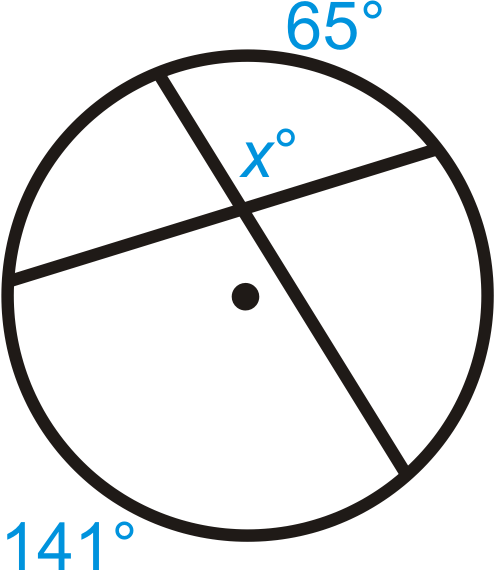
   Figura\(\PageIndex{8}\)

2. 

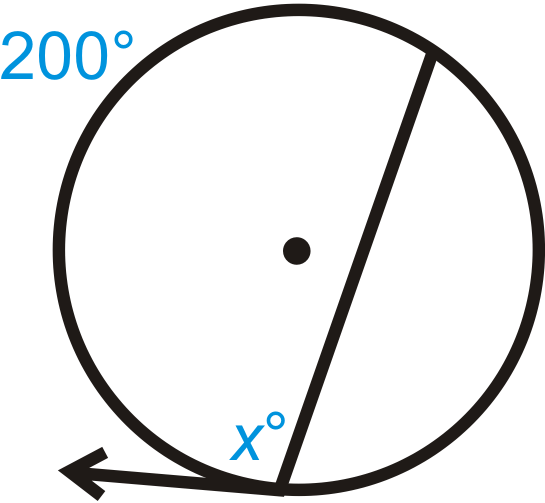
   Figura\(\PageIndex{9}\)

3. 

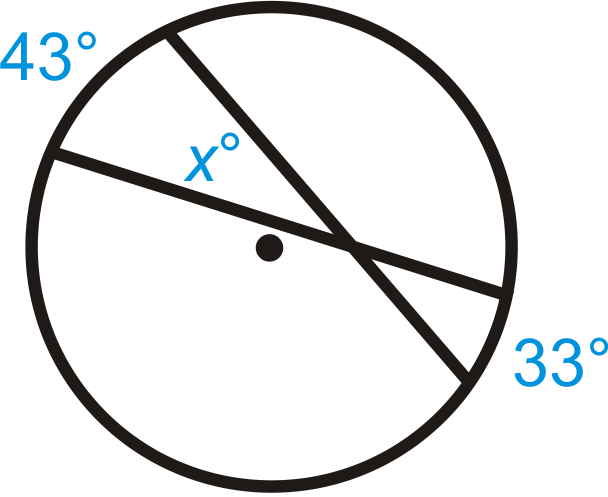
   Figura\(\PageIndex{10}\)

4. 

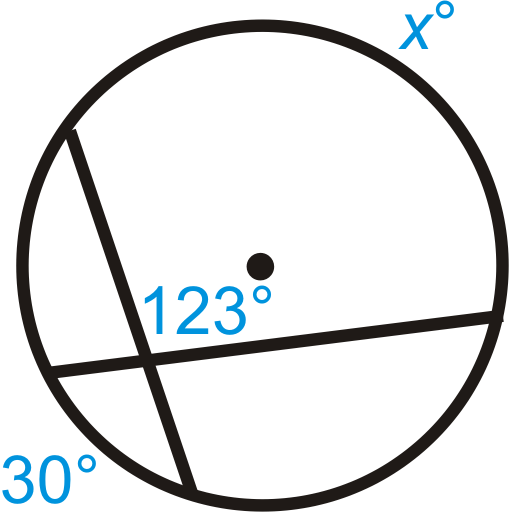
   Figura\(\PageIndex{11}\)

5. 

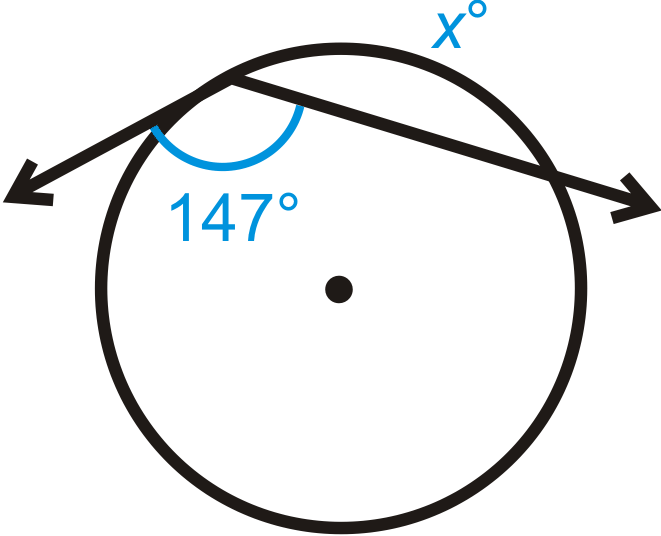
   Figura\(\PageIndex{112}\)

6. 

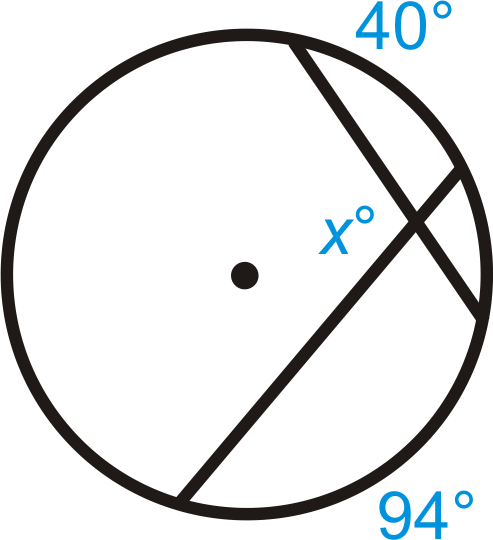
   Figura\(\PageIndex{13}\)

7. \(y\neq 60^{\circ}\)

   

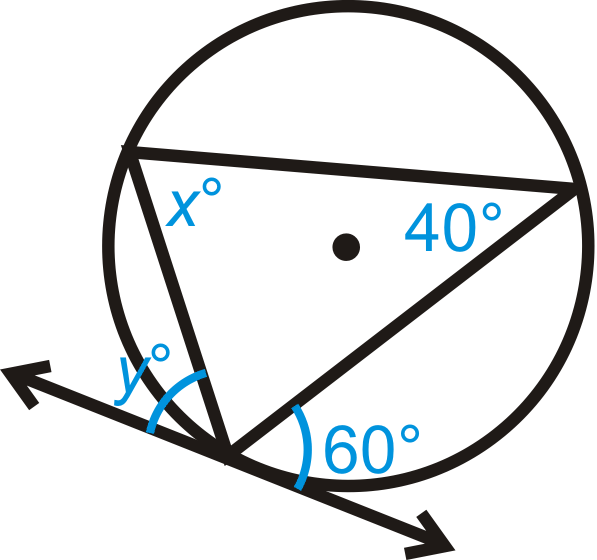
   Figura\(\PageIndex{14}\)

Resolver para\(x\).

8. Rellenar los espacios en blanco de la prueba para el Teorema del Ángulo de Acordes Intersecantes

   

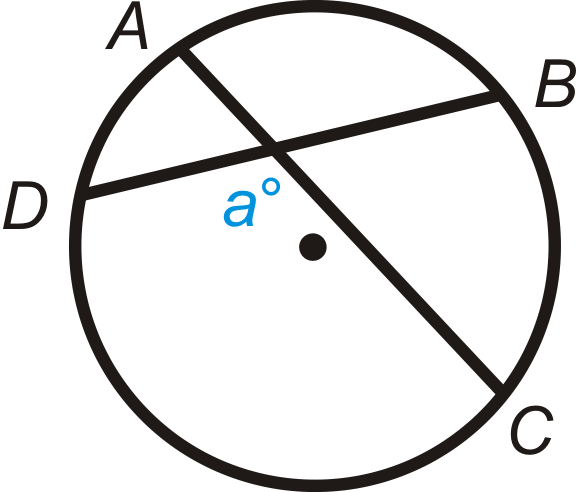
   Figura\(\PageIndex{15}\)

Dado: Acordes de intersección\(\overline{AC}\) y\(\overline{BD}\).

Demostrar:\(m\angle a=\dfrac{1}{2}(m\widehat{DC}+m\widehat{AB})\)

Declaración	Razón
1. Acordes que se cruzan\(\overline{AC}\) y\(\overline{BD}\).	1.
2. Sorteo\(\overline{BC}\) 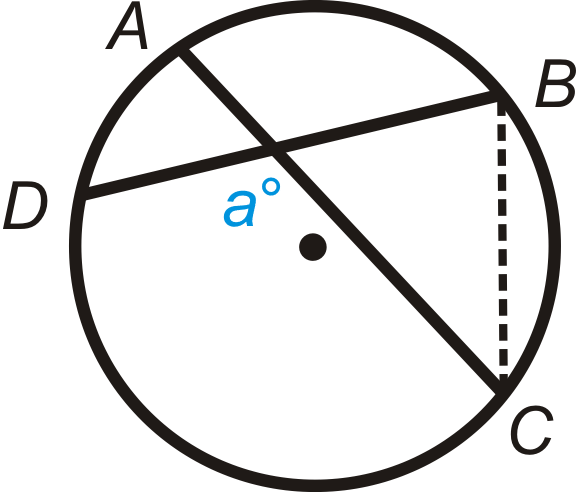Figura\(\PageIndex{16}\)	2. Construcción
3. \(m\angle DBC=\dfrac{1}{2}m\widehat{DC}\) \(m\angle ACB=\dfrac{1}{2}m\widehat{AB}\)	3.
4. \(m\angle a=m\angle DBC+m\angle ACB\)	4.
5. \(m\angle a=\dfrac{1}{2}m\widehat{DC}+\dfrac{1}{2}m\widehat{AB}\)	5.

Rellene los espacios en blanco.

9. Si el vértice de un ángulo es _______________ un círculo, entonces su medida es el promedio de los arcos __________________.
10. Si el vértice de un ángulo es ________ un círculo, entonces su medida es ______________ el arco interceptado.

vocabulario

Término	Definición
ángulo central	Un ángulo formado por dos radios y cuyo vértice se encuentra en el centro del círculo.
acorde	Un segmento de línea cuyos extremos están en un círculo.
círculo	El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro.
diámetro	Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio.
ángulo inscrito	Un ángulo con su vértice en el círculo y cuyos lados son acordes.
arco interceptado	El arco que se encuentra dentro de un ángulo inscrito y cuyos extremos están en el ángulo.
punto de tangencia	El punto donde la línea tangente toca el círculo.
radio	La distancia desde el centro hasta el borde exterior de un círculo.
Teorema de Ángulo de Acorde/Tangente	El Teorema del Ángulo Acorde/Tangente establece que la medida de un ángulo formado por una cuerda y una tangente que se cruzan en un círculo es la mitad de la medida del arco interceptado.
Teorema de ángulo de acordes de intersección	El Teorema del Ángulo de Acordes Intersectados establece que la medida del ángulo formado por dos acordes que se cruzan dentro de un círculo es el promedio de las medidas de los arcos interceptados.

Recursos adicionales

Elemento interactivo

Video: Principios de ángulos dentro y dentro de un círculo - Básico

Actividades: Ángulos dentro y dentro de un círculo Preguntas de discusión

Ayudas de estudio: Guía de estudio de arcos y ángulos

Práctica: Ángulos dentro y dentro de un círculo