6.9: Arcos en Círculos
- Page ID
- 107230
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Secciones de círculo y ángulos centrales.
Un círculo tiene\(360^{\circ}\). Un arco es una sección del círculo. Un semicírculo es un arco que mide\(180^{\circ}\).
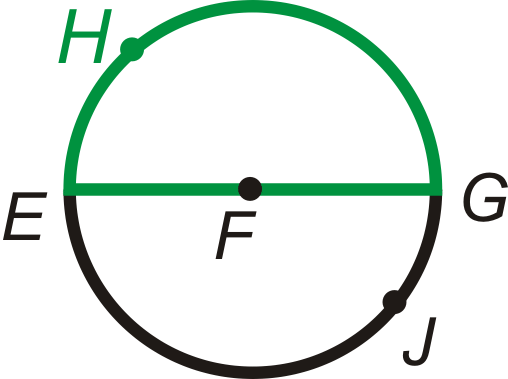
\(\widehat{EHG}\)y\(\widehat{EJG}\) son semicírculos
Un ángulo central es el ángulo formado por dos radios con su vértice en el centro del círculo. Un arco menor es un arco que es menor que\(180^{\circ}\). Un arco mayor es un arco que es mayor que\(180^{\circ}\). Siempre use 3 letras para etiquetar un arco mayor.
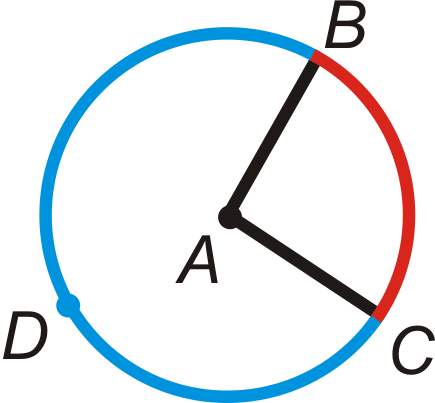
El ángulo central es\(\angle BAC\). El arco menor es\(\widehat{BC}\). El arco mayor es\(\widehat{BDC}\).
Un arco se puede medir en grados o en una medida lineal (cm, ft, etc.). En este concepto utilizaremos medida de grado. La medida de un arco menor es la misma que la medida del ángulo central que le corresponde. La medida de un arco mayor es\(360^{\circ}\) menos la medida del arco menor correspondiente. La medida del arco formado por dos arcos adyacentes es la suma de las medidas de los dos arcos (Postulado de Adición de Arco).
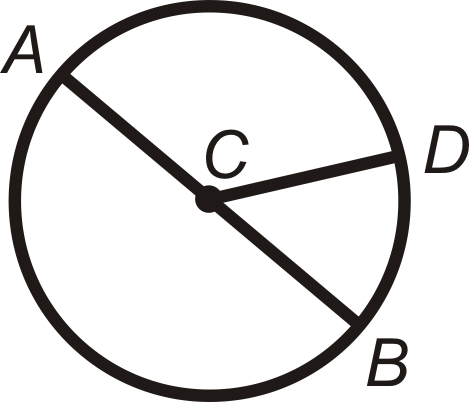
\(m\widehat{AD}+m\widehat{DB}=m\widehat{ADB}\)
¿Y si un círculo se dividiera en pedazos por varios radios? ¿Cómo se pudieron encontrar las medidas de los arcos formados por estos radios?
Ejemplo\(\PageIndex{1}\)
Encuentra\(m\widehat{AB}\) y\(m\widehat{ADB}\) en\(\bigodot C\).
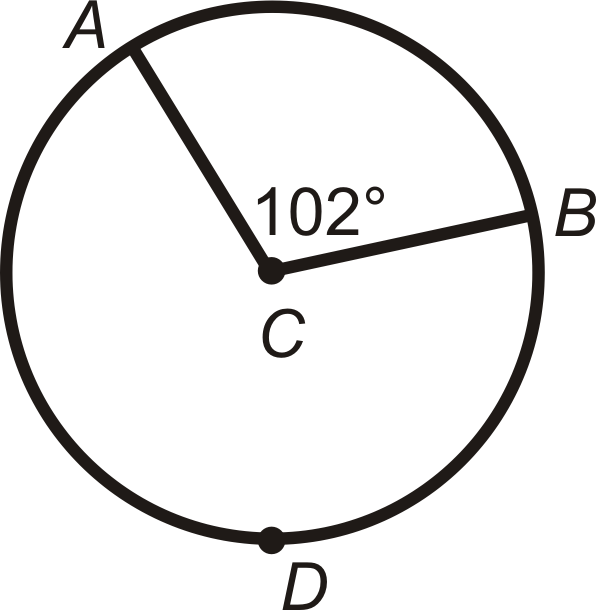
Solución
\(m\widehat{AB}=m\angle ACB\). Entonces,\(m\widehat{AB}=102^{\circ}\).
\(m\widehat{ADB}=360^{\circ}−m\widehat{AB}=360^{\circ}−102^{\circ}=258^{\circ}\)
Ejemplo\(\PageIndex{2}\)
Encuentra las medidas de los arcos menores en\(\bigodot A\). \(\overline{EB}\)es un diámetro.
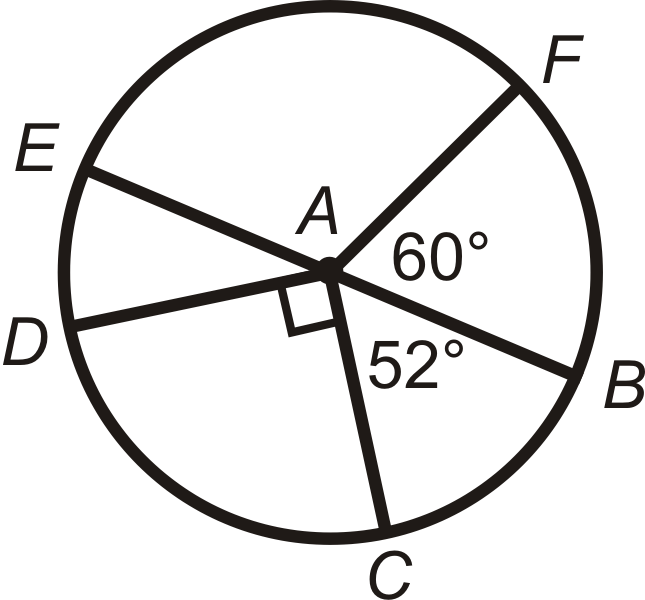
Solución
Porque\(\overline{EB}\) es un diámetro,\(m\angle EAB=180^{\circ}\). Cada arco tiene la misma medida que su ángulo central correspondiente.
\(\begin{aligned} m\widehat{BF}&=m\angle FAB=60^{\circ} \\ m\widehat{EF}&=m\angle EAF=120^{\circ}\rightarrow 180^{\circ}−60^{\circ} \\ m\widehat{ED}&=m\angle EAD=38^{\circ} \rightarrow 180^{\circ}−90^{\circ}−52^{\circ} \\ m\widehat{DC}&=m\angle DAC=90^{\circ} \\ m\widehat{BC}&=m\angle BAC=52^{\circ}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra las medidas de los arcos indicados en\(\bigodot A\). \(\overline{EB}\)es un diámetro.

Usa el Postulado de Adición de Arco.
- \(m\widehat{FED}\)
- \(m\widehat{CDF}\)
- \(m\widehat{DFC}\)
Solución
- \(m\widehat{FED}=m\widehat{FE}+m\widehat{ED}=120^{\circ}+38^{\circ}=158^{\circ}\)
- \(m\widehat{CDF}=m\widehat{CD}+m\widehat{DE}+m\widehat{EF}=90^{\circ}+38^{\circ}+120^{\circ}=248^{\circ}\)
- \(m\widehat{DFC}=m\widehat{ED}+m\widehat{EF}+m\widehat{FB}+m\widehat{BC}=38^{\circ}+120^{\circ}+60^{\circ}+52^{\circ}=270^{\circ}\)
Ejemplo\(\PageIndex{4}\)
Enumere los arcos congruentes a\(\bigodot C\) continuación. \(\overline{AB}\)y\(\overline{DE}\) son diámetros.
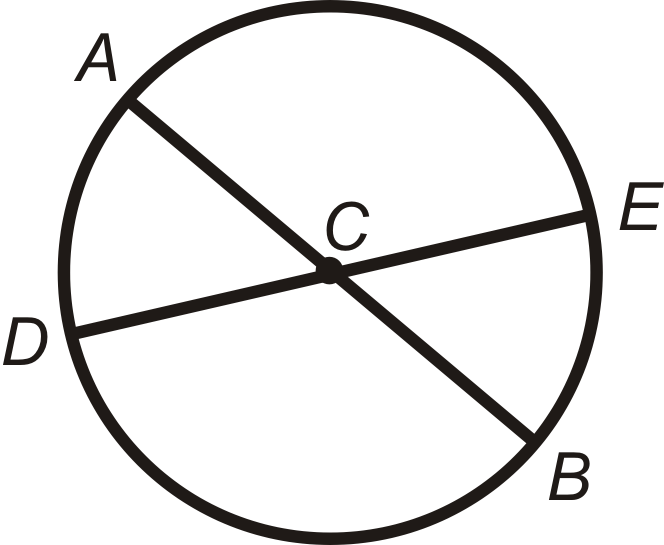
Solución
\(\angle ACD\cong \angle ECB\)porque son ángulos verticales. \(\angle DCB\cong \angle ACE\)porque también son ángulos verticales.
\(\widehat{AD}\cong \widehat{EB}\)y\(\widehat{AE}\cong \widehat{DB}\)
Ejemplo\(\PageIndex{5}\)
Para cada uno de los círculos de abajo, ¿son congruentes los arcos azules? Explique por qué o por qué no.
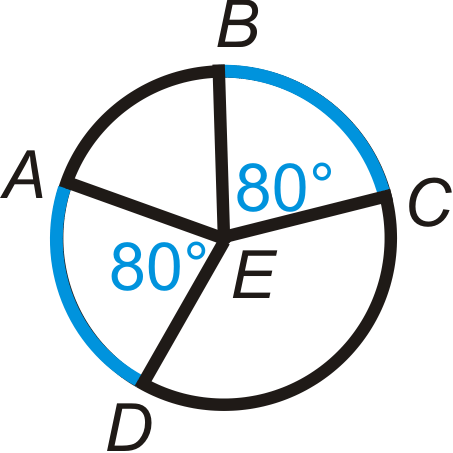
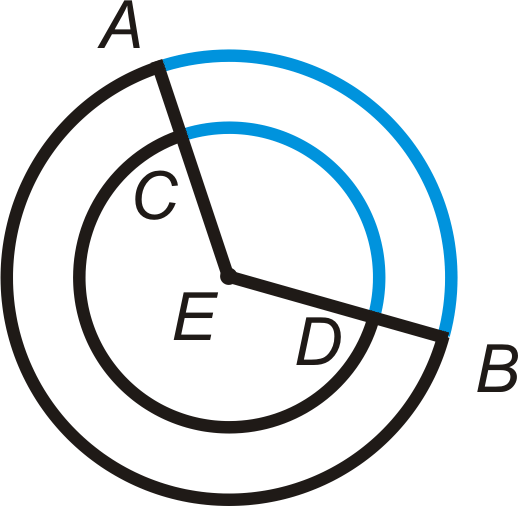
Solución
Para el primer círculo,\(\widehat{AD}\cong \widehat{BC}\) porque tienen la misma medida de ángulo central y están en el mismo círculo.
Para el segundo círculo, los dos arcos tienen la misma medida, pero no son congruentes porque los círculos tienen radios diferentes.
Revisar
Determine si los arcos a continuación son un arco menor, arco mayor o semicírculo de\(\bigodot G\). \(\overline{EB}\)es un diámetro.
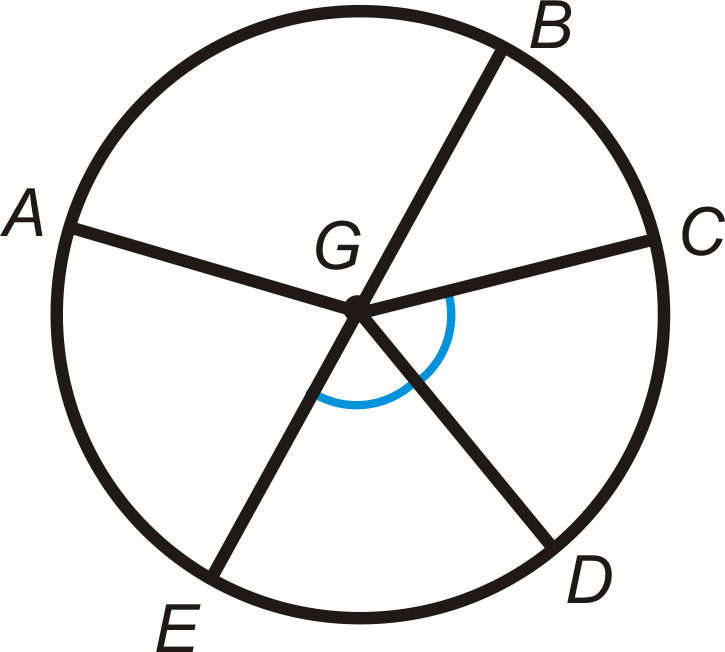
- \(\widehat{AB}\)
- \(\widehat{ABD}\)
- \(\widehat{BCE}\)
- \(\widehat{CAE}\)
- \(\widehat{ABC}\)
- \(\widehat{EAB}\)
- ¿Hay arcos congruentes? Si es así, enumérelos.
- Si\(m\widehat{BC}=48^{\circ}\), encuentra m\ anchohat {CD}\).
- Usando #8, encuentra m\ anchohat {CAE}\).
Encuentra la medida del arco menor y el arco mayor en cada círculo a continuación.
-
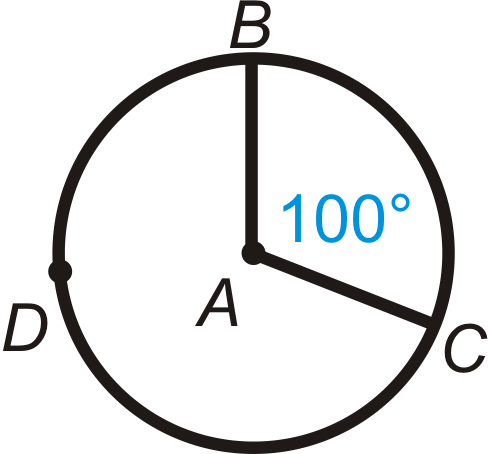
Figura\(\PageIndex{11}\) -
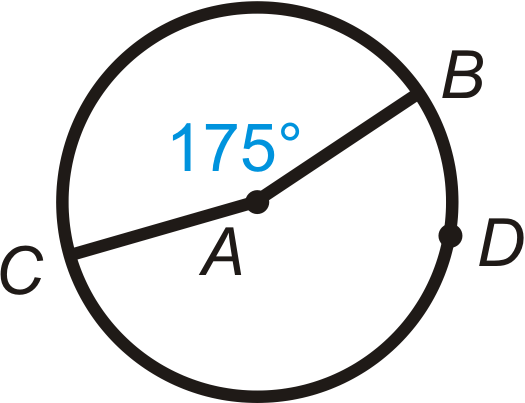
Figura\(\PageIndex{12}\) -
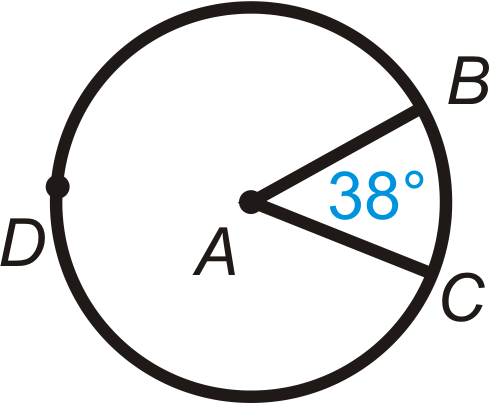
Figura\(\PageIndex{13}\) -
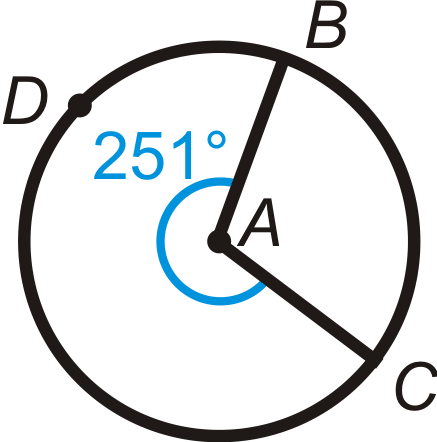
Figura\(\PageIndex{14}\) -
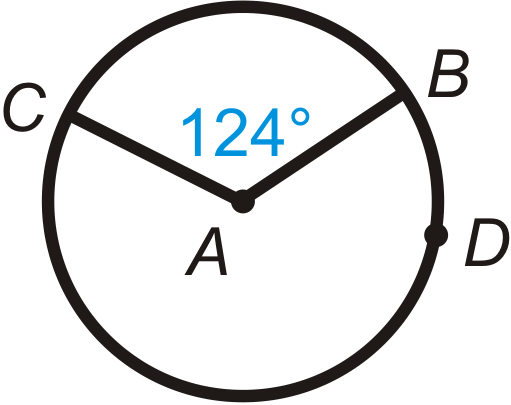
Figura\(\PageIndex{15}\) -
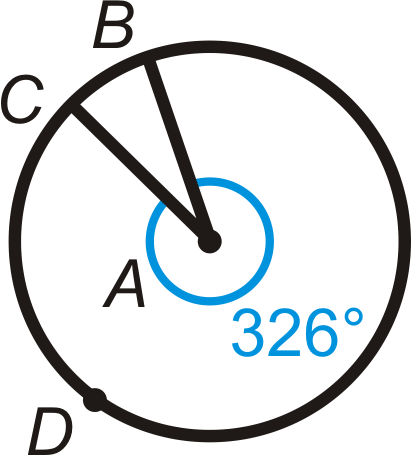
Figura\(\PageIndex{16}\)
Determinar si los arcos azules son congruentes. Si es así, indícales por qué.
-
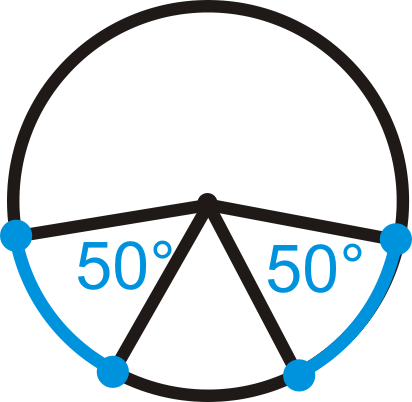
Figura\(\PageIndex{17}\)
-

Figura\(\PageIndex{17}\)
-

Figura\(\PageIndex{17}\)
Encuentra la medida de los arcos o ángulos centrales indicados en\ bigodot A\). \ overline {DG}\) es un diámetro.
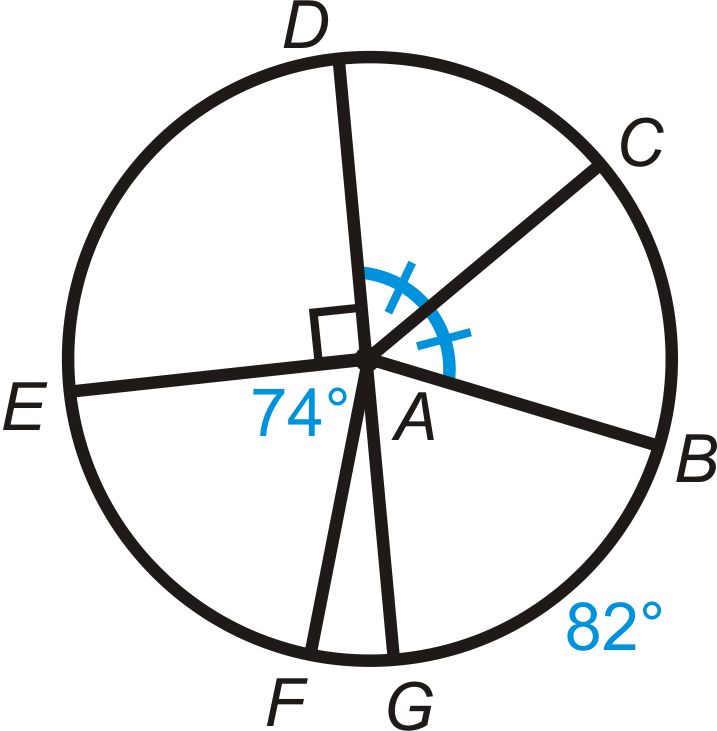
- \ anchohat {DE}\)
- \ anchohat {DC}\)
- \ anchohat {GAB}\)
- \ anchohat {FG}\)
- \ sombrero de ancho{ EDB}
- \ anchohat {EAB}\)
- \ anchohat {DCF}\)
- \ anchohat {DBE}\)
Encuentra la medida de x\) en\ bigodot P\).
-
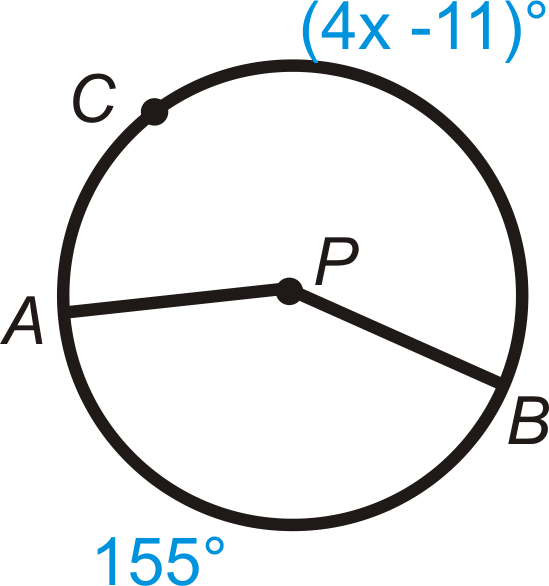
Figura\(\PageIndex{19}\) -
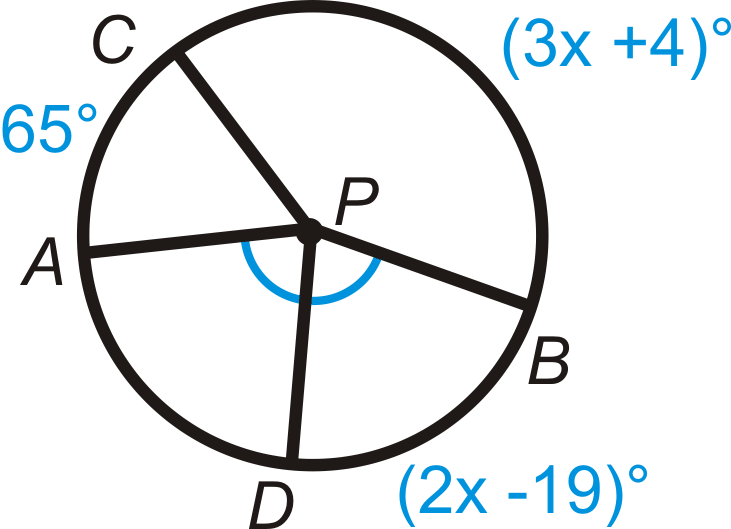
Figura\(\PageIndex{20}\) -
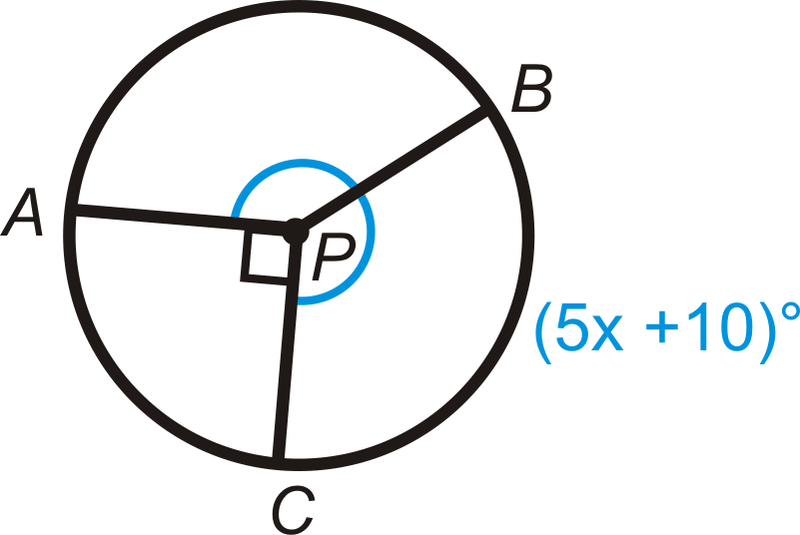
Figura\(\PageIndex{21}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.3.
El vocabulario
| Término | Definición |
|---|---|
| arco | Una sola sección del círculo, que describe un ángulo particular. |
| ángulo central | Un ángulo formado por dos radios y cuyo vértice se encuentra en el centro del círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| arco mayor | Un arco que es mayor que\(180^{\circ}\). |
| arco menor | Un arco que es menor que\(180^{\circ}\). |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
| semicírculo | Un arco que mide\(180^{\circ}\). |
| Postulado de Adición de Arco | El postulado de adición de arco establece que la medida del arco formado por dos arcos adyacentes es la suma de las medidas de los dos arcos. |
| Diámetro | El diámetro es la medida de la distancia a través del centro de un círculo. El diámetro es igual al doble de la medida del radio. |
Recursos adicionales
Elemento Interactivo
Video: Arcos en Círculos Principios - Básicos
Actividades: Arcos en Círculos Preguntas de Discusión
Ayudas de estudio: Propiedades de una guía de estudio circular
Práctica: Arcos en Círculos
Mundo real: Cultivo del Arco

