6.4: Circunferencia
- Page ID
- 107220
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra la circunferencia de un círculo usando las fórmulas:\(C = \pi d\);\(C = 2\pi r\).
Circunferencia es la distancia alrededor de un círculo. La circunferencia también se puede llamar el perímetro de un círculo. Sin embargo, usamos el término circunferencia para los círculos porque son redondos.
Fórmula Circunferencia:\(C=\pi d\) donde el diámetro\(d=2r\), o el doble del radio. Entonces\(C=2\pi r\) también.
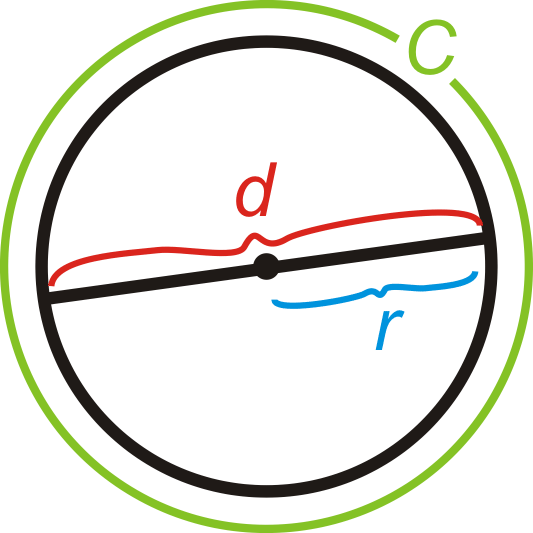
\(\pi\), o “pi” es la relación entre la circunferencia de un círculo y su diámetro. Es aproximadamente igual a 3.14159265358979323846...
Deberías tener un botón\ pi en tu calculadora. Si no lo haces, puedes usar 3.14 como aproximación para\(\pi\). También puedes dejar tus respuestas en términos de\(\pi\) para muchos problemas.
¿Y si te dieran el radio o diámetro de un círculo? ¿Cómo pudiste encontrar la distancia alrededor de ese círculo?
Ejemplo\(\PageIndex{1}\)
Encuentra la circunferencia de un círculo con un radio de 7 cm.
Solución
Enchufe el radio en la fórmula.
\(C=2\pi (7)=14\pi \approx 44\text{ cm }\)
Ejemplo\(\PageIndex{2}\)
La circunferencia de un círculo es\(64\pi\) unidades. Encuentra el diámetro.
Solución
De nuevo, puedes enchufar lo que sabes en la fórmula de circunferencia y resolverlo\(d\).
\(\begin{aligned} 64\pi =\pi d \\ 64\text{ units }=d\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Un círculo se inscribe en un cuadrado con 10 pulg. lados. ¿Cuál es la circunferencia del círculo? Deja tu respuesta en términos de\(\pi\).
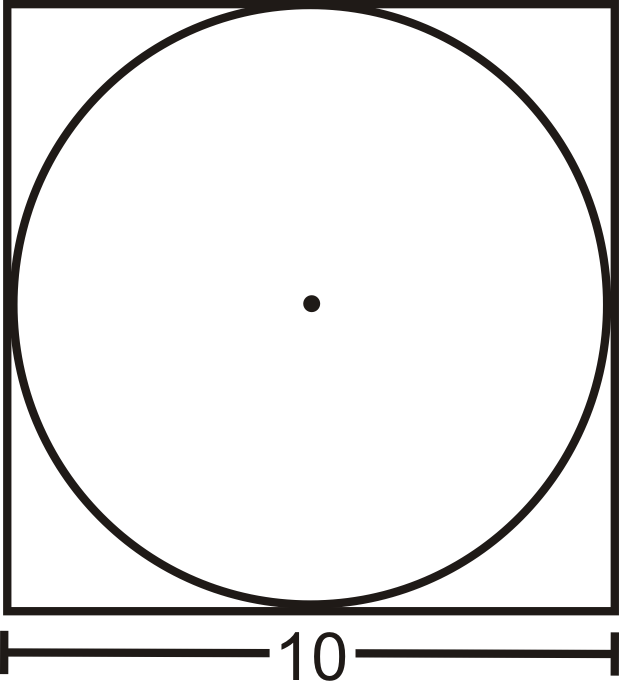
Solución
De la imagen, podemos ver que el diámetro del círculo es igual a la longitud de un lado. \(C=10\pi \text{ in. }\)
Ejemplo\(\PageIndex{4}\)
Encuentra el perímetro de la plaza en el Ejemplo 3. ¿Es más o menos que la circunferencia del círculo? ¿Por qué?
Solución
El perímetro es\(P=4(10)=40\text{ in. }\) Para poder comparar el perímetro con la circunferencia debemos cambiar la circunferencia a un decimal.
\(C=10\pi \approx 31.42 \text{ in. }\)Esto es menor que el perímetro de la plaza, lo que tiene sentido porque el círculo está dentro de la plaza.
Ejemplo\(\PageIndex{5}\)
Las llantas de un automóvil compacto son de 18 pulgadas de diámetro. ¿A qué distancia recorre el automóvil después de que las llantas giran una vez? ¿A qué distancia recorre el automóvil después de 2500 rotaciones de las llantas?
Solución
Una vuelta de la llanta es la circunferencia. Esto sería\(C=18\pi \approx 56.55\text{ in. }\) 2500 rotaciones serían\(2500\cdot 56.55\) aproximadamente 141,375 pulgadas, 11,781 pies, o 2.23 millas.
Revisar
Rellena la siguiente tabla. Deja todas las respuestas en términos de\(\pi\).
| diámetro | radio | circunferencia | |
|---|---|---|---|
| 1. | 15 | ||
| 2. | 4 | ||
| 3. | 6 | ||
| 4. | \(84\pi\) | ||
| 5. | 9 | ||
| 6. | \(25\pi\) | ||
| 7. | \(2\pi\) | ||
| 8. | 36 |
- Encuentra la circunferencia de un círculo con\(d=\dfrac{20}{\pi} \text{ cm }\).
\(PQSR\)La plaza está inscrita en\(\bigodot T\). \(RS=8\sqrt{2}\).
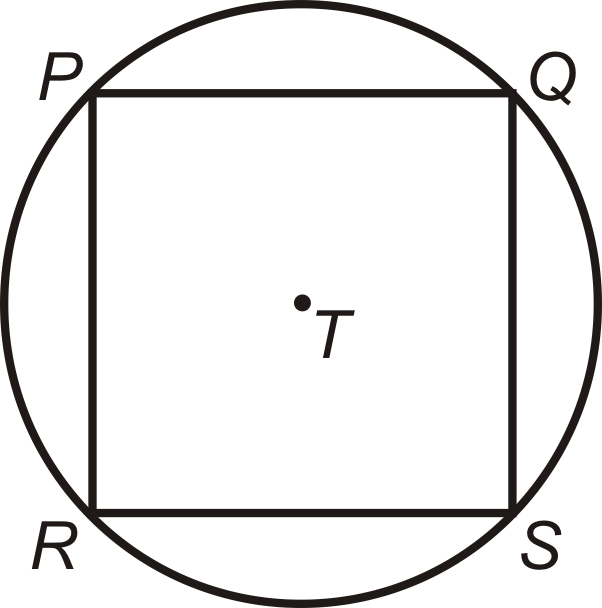
- Encuentra la longitud del diámetro de\(\bigodot T\).
- ¿Cómo se relaciona el diámetro\(PQSR\)?
- Encuentra el perímetro de\(PQSR\).
- Encuentra la circunferencia de\(\bigodot T\).
Para las preguntas 14-17, una camioneta tiene llantas con un diámetro de 26.
- ¿Qué tan lejos recorre la camioneta cada vez que una llanta gira exactamente una vez? ¿Qué es lo mismo que esto?
- ¿Cuántas veces girará la llanta después de que la camioneta recorra 1 milla? (1 milla = 5280 pies)
- El camión ha recorrido 4072 rotaciones de llantas. ¿Cuántas millas es esta?
- La recomendación promedio para la vida útil de una llanta es de 30,000 millas. ¿Cuántas rotaciones es esta?
vocabulario
| Término | Definición |
|---|---|
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| Circunferencia | La circunferencia de un círculo es la medida de la distancia alrededor del borde exterior de un círculo. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| pi | (o\(\pi\)) La relación entre la circunferencia de un círculo y su diámetro. |
| Radio | El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Polígono Regular | Un polígono regular es un polígono con todos los lados de la misma longitud y todos los ángulos la misma medida. |
Recursos adicionales
Elemento Interactivo
Video: Circunferencia de un Círculo
Actividades: Preguntas de discusión sobre circunferencia
Ayudas de estudio: Guía de estudio de circunferencia y longitud de arco
Práctica: Circunferencia
Mundo real: Una rotonda de camino a casa