1.1:1.1 Familias de funciones
- Page ID
- 107334
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las funciones vienen en todas las formas diferentes. Algunos están muy estrechamente relacionados y otros son muy diferentes, pero a menudo confundidos. Por ejemplo, ¿cuál es la diferencia entre\(x^{2}\) y\(2^{x}\)? Ambos tienen un\(x\) y un 2 y ambos equivalen a 4 cuando\(x=2\), pero uno finalmente se vuelve mucho más grande que el otro.
Familias de Funciones
Si los matemáticos son cocineros, entonces las familias de funciones son sus ingredientes. Cada familia de funciones tiene su propio sabor y personalidad. Antes de aprender a combinar funciones para crear un número infinito de modelos potenciales, es necesario tener una idea clara del nombre de cada familia de funciones y cómo actúa.
La función de identidad:\(f(x)=x\)
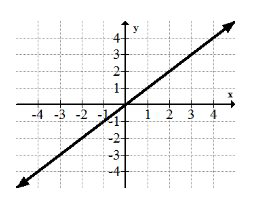
La función de identidad es la función más simple y todas las líneas rectas son transformaciones de la familia de funciones de identidad.
La función de cuadratura:\(f(x)=x^{2}\)
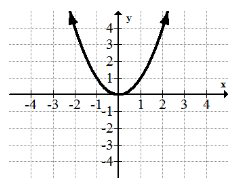
La función de cuadratura (función cuadrática) se llama comúnmente parábola y es útil para modelar el movimiento de objetos que caen. Todas las parábolas son transformaciones de esta función de cuadratura.
La función Cubing:\(f(x)=x^{3}\)
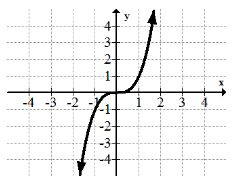
La función de cubo tiene un tipo de simetría diferente a la función de cuadratura. Dado que el volumen se mide en unidades cúbicas, muchas aplicaciones de física utilizan la función cúbica.
La función de raíz cuadrada:\(f(x)=\sqrt{x}=x^{\frac{1}{2}}\)
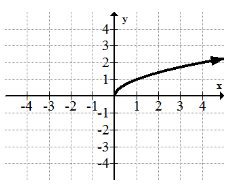
La función raíz cuadrada no está definida sobre todos los números reales. Introduce la posibilidad de números complejos y también está estrechamente relacionado con la función de cuadratura.
La función recíproca:\(f(x)=x^{-1}=\frac{1}{x}\)
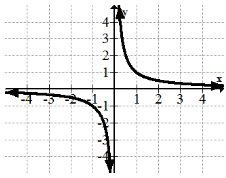
La función recíproca también se conoce como hipérbola y función racional. Tiene dos partes que están desconectadas y no se define a cero. Los circuitos eléctricos simples se modelan con la función recíproca.
Hasta ahora todas las funciones se pueden agrupar en una familia de funciones aún más grande llamada familia de funciones de poder.
La familia de funciones de potencia:\(f(x)=c x^{a}\)
La familia de funciones de potencia tiene dos parámetros. El parámetro\(c\) es un factor de escala vertical. El parámetro\(a\) controla todo sobre la forma. La razón por la que todas las funciones hasta ahora son subconjuntos de la familia de funciones de poder más grande es porque solo difieren en su valor de\(a\). La familia de funciones de poder también te muestra que hay un número infinito de otras funciones como los cuartics\(\left(f(x)=x^{4}\right)\) y los quínticos\(\left(f(x)=x^{5}\right)\) que realmente no necesitan toda una categoría propia. La familia de funciones de potencia se puede ampliar para crear polinomios y funciones racionales.
La familia de funciones exponenciales:\(f(x)=e^{x}\)
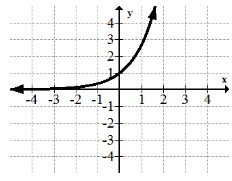
La familia de funciones exponenciales es una de las primeras funciones que ves donde no\(x\) está la base del exponente. Esta función eventualmente crece mucho más rápido que cualquier función de potencia. \(f(x)=2^{x}\)es también una función exponencial muy común. Muchas aplicaciones como la biología y las finanzas requieren el uso del crecimiento exponencial.
La función del logaritmo:\(f(x)=\ln x\)
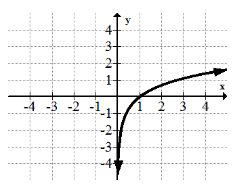
La función logarítmica está estrechamente relacionada con la familia de funciones exponenciales. Muchas personas confunden la gráfica de la función log con la función de raíz cuadrada. Un análisis cuidadoso mostrará varias diferencias importantes. La función log es la base de la Escala Richter que es como se miden los sismos.
La familia de funciones periódicas:\(f(x)=\sin x\)
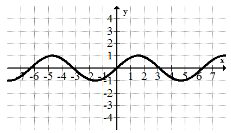
La gráfica sinusoidal es una de las muchas funciones periódicas. Periódica se refiere al hecho de que la onda sinusoidal repite un ciclo cada periodo de tiempo. Las funciones periódicas son extremadamente importantes para modelar mareas y otros fenómenos del mundo real.
La función de valor absoluto:\(f(x)=|x|\)
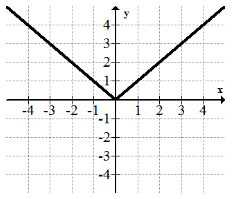
La función de valor absoluto es una de las pocas funciones básicas que no es totalmente fluida.
La función logística:\(f(x)=\frac{1}{1+e^{-x}}\)
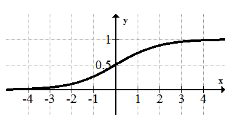
La función logística es una combinación de la función exponencial y la función recíproca. Esta curva es muy potente porque modela crecimientos poblacionales donde la población máxima está limitada por los recursos ambientales.
Ejemplos
Antes, se le dio un problema de comparar\(x^{2}\) y\(2^{x}\). Si bien\(x^{2}\) y\(2^{x}\) tienen ingredientes similares, tienen características gráficas muy diferentes. La función de cuadratura es simétrica alrededor de la línea\(x=0\) mientras que la función exponencial no lo es. Cuando\(x=0\), la función de cuadratura tiene una altura de cero y la función exponencial tiene una altura de uno. La función de cuadratura tiene una pendiente que se vuelve más pronunciada a medida que se\(x\) va alejando del origen mientras que la función exponencial se aplana a medida que\(x\) se vuelve muy pequeña. Todas estas diferencias son importantes y no obvias a primera vista.
\(y=x\),\(y=e^{x}\),\(y=\frac{1}{1+e^{-x}} .\) Algunas funciones que están cerca pero no del todo:\(y=x^{3}\),\(y=\sqrt{x}\)
Compara y contrasta las gráficas de las dos funciones:
\(f(x)=\ln x\)y\(h(x)=\sqrt{x}\)
Similitudes: Ambas funciones aumentan sin límite a medida que\(x\) se hace más grande. Ambas funciones no están definidas para números negativos.
Diferencias: La función log se acerca al infinito negativo cuando se\(x\) acerca a 0. La función raíz cuadrada, por otro lado, apenas termina en el punto (0,0).
Describir la simetría entre las familias de funciones discutidas en este concepto. Considere la simetría de reflexión y la simetría rotacional.
Algunas familias de funciones tienen simetría reflexiva consigo mismas:
\(y=x\),\(y=x^{2}\),\(y=\frac{1}{x}\),\(y=|x|\)
Algunas familias de funciones son rotacionalmente simétricas:
\(y=x\),\(y=x^{3}\),\(y=\frac{1}{x}\),\(y=\sin x\),\(y=\frac{1}{1+e^{-x}}\)
Algunos pares de familias de funciones son reflexiones completas o parciales de otras familias de funciones:
\(y=x^{2}\),\(y=\sqrt{x}\)
\(y=e^{x}\),\(y=\ln x\)
Revisar
Para 1-10, esboce una gráfica de la función desde la memoria.
1. \(y=e^{x}\)
2. \(y=\ln (x)\)
3. \(y=\sin (x)\)
4. \(y=x^{2}\)
5. \(y=|x|\)
6. \(y=\frac{1}{x}\)
7. \(y=\frac{1}{1+e^{-x}}\)
8. \(y=\sqrt{x}\)
9. \(y=x^{3}\)
10. \(y=x\)
11. ¿Qué función no está definida en 0? ¿Por qué?
12. ¿Qué funciones están delimitadas a continuación pero no por encima?
13. ¿Cuáles son las diferencias entre\(y=x^{2}\) y\(y=x^{3}\)?
14. ¿Qué es una similitud entre\(y=e^{x}\) y\(y=\ln (x)\)?
15. Explicar por qué no\(y=\sqrt{x}\) se define para todos los valores de\(x\).

