1.4:1.4 Dominio y Rango
- Page ID
- 107343
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Analizar medios para examinar metódicamente y en detalle. Una forma de analizar funciones es observando posibles entradas (dominio) y posibles salidas (rango). ¿Cuáles de las funciones básicas tienen dominios limitados y por qué?
Dominio y Rango
Notación
El dominio y el rango se describen en notación de intervalos. Paréntesis, (), media no inclusiva. Corchetes, [], significan inclusivo. Las siguientes descripciones de números en notación de intervalo se han convertido en notación de intervalo.
1. Todos los números.
\((-\infty, \infty)\)Nota: Los paréntesis siempre se usan con infinito.
2. Todos los números negativos sin incluir 0.
\((-\infty, 0)\)
3. Todos los números positivos incluyendo 0.
\([0, \infty)\)
4. Cada número entre 1 y 4 incluyendo 1 y 4.
[1,4]
5. Cada número entre 5 y 6 sin incluir 5 o 6.
(5, 6)
6. Los números 1 a 2 incluyendo 1 pero sin incluir 2 y los números
10 a 25 incluyendo ambos 10 y 25
[1,2)\(\cup[10,25]\)
Nota: El\(\cup\) símbolo significa Unión y se refiere al hecho de que si algún número\(x\) está en esta unión, entonces está o bien en el primer grupo o está en el segundo grupo. Este símbolo está asociado con la sentencia OR. Si bien es cierto que el símbolo de la Unión parece unir a un grupo y a otro, el símbolo para Y es el\(\cap\) que significa intersección. La intersección es diferente de la unión porque intersección significa todos los números que están tanto en el primer grupo como en el segundo grupo al mismo tiempo.
Dominio y Dominio Restringido
Dominio son las posibles entradas a una función. Muchas funciones permiten introducir cualquier tipo de números. Esto incluye números que son positivos, negativos, cero, fracciones o decimales. La función de cuadratura\(y=x^{2}\) es un ejemplo que tiene un dominio de todos los números reales posibles. Tres funciones tienen restricciones muy específicas:
La función de raíz cuadrada: Restricción de\(y=\sqrt{x}\)
dominio:\(x \geq 0\)
Esto se debe a que la raíz cuadrada de un número negativo no es un número real. Esta restricción se puede observar en la gráfica porque la curva termina en el punto (0,0) y no se define en ningún lugar donde\(x\) sea negativa.
La función log solo se define en números que son estrictamente mayores que cero. Esto se debe a que la función logarítmica es una forma diferente de escribir exponentes. Una propiedad de los exponentes es que cualquier número positivo elevado a cualquier potencia nunca producirá un número negativo o cero. La restricción se puede observar en la gráfica por la forma en que la función log se acerca a la línea vertical\(x=0\) y dispara hasta el infinito.
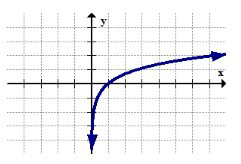
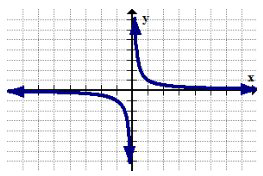
La función recíproca: Restricción de\(y=\frac{1}{x}\)
dominio:\(x \neq 0\)
La función recíproca está restringida porque no se pueden dividir números por cero. Cualquier\(x\) valor que haga que el denominador de una función sea cero están fuera del dominio. Esta restricción se puede observar en la gráfica por la forma en que la función recíproca nunca toca la línea vertical\(x=0\).
Rango
Rango son las posibles salidas de una función. Prácticamente cualquier función puede producir cualquier salida mediante el uso de transformaciones y, por lo tanto, determinar el rango de una función es significativamente menos procedimental que determinar el dominio. Usa lo que sabes sobre la forma de cada función y sus ecuaciones para decidir qué\(y\) valores son posibles de producir y qué\(y\) valores son imposibles de producir.
Búsqueda de dominio y rango
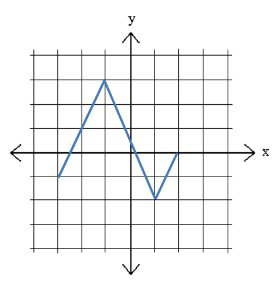
El dominio y el rango para la gráfica anterior son:
Dominio:\(x \in[-3,2]\)
Rango:\(y \in[-2,3]\)
Tenga en cuenta que el\(\in\) símbolo significa “es un elemento de” y significa que el\(x\) o el\(y\) está en ese intervalo y los números en el intervalo siempre se escriben en orden creciente. [3, -2] se considera impropio.
Tenga en cuenta que aunque el [-3,2] pueda parecer similar al par ordenado que representa el punto donde\(x=-3\) y\(y=2,\) este no es el caso. Tanto el -3 como el 2 son\(x\) valores. Este concepto erróneo es por lo que siempre debes escribir\(x \in\) porque te recuerda este hecho. Muchas personas se confunden mucho cuando ven algo así\(x \in(-2,1)\) porque ven el paréntesis e inmediatamente ven un punto en el que deberían ver un intervalo en el\(x\) eje.
En la gráfica de abajo, hay dos piezas diferentes de la función.
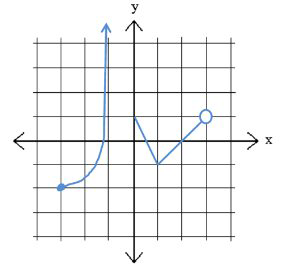
El dominio y el rango para la gráfica anterior son:
Dominio:\(x \in[-3,-1) \cup[0,3)\)
Rango:\(y \in[-2, \infty)\)
La función parece acercarse a la línea vertical\(x=-1\) sin llegar realmente a ella se utiliza\(s 0\) un corchete abierto. También, el agujero vacío en el punto\((3,\) 1) por lo que el dominio excluye el\(x\) valor de 3.
Ejemplos
Anteriormente, se le preguntó qué funciones básicas tienen dominios limitados. Las tres funciones que tienen dominios limitados son la función raíz cuadrada, la función log y la función recíproca. La función raíz cuadrada tiene un dominio restringido porque no se pueden tomar raíces cuadradas de números negativos y producir números reales. La función log está restringida porque la función log no está definida para operar en números no positivos. La función recíproca está restringida porque los números que se dividen por cero no están definidos.
Identificar el dominio y rango de la siguiente función escrita en una tabla:
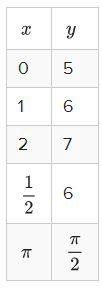
La ecuación específica de la función puede estar oculta, pero de la tabla se puede determinar el dominio y el rango directamente a partir de los\(y\) valores\(x\) y. Puede ser tentador adivinar que otros valores podrían funcionar potencialmente en la tabla, especialmente si el patrón es obvio, pero este no es el tipo de pregunta que plantea cuál podría ser la función. En cambio esta pregunta solo pregunta cuál es el dominio y el rango declarados.
Dominio:\(x \in\left\{0,1,2, \frac{1}{2}, \pi\right\}\)
Rango:\(y \in\left\{5,6,7, \frac{\pi}{2}\right\}\)
Observe que los dos 6's que aparecen en la tabla no necesitan ser escritos dos veces en el rango.
Identificar el dominio de las siguientes tres funciones transformadas.
1. \(y=10 \sqrt{2-x}-3\)
El argumento de la función debe ser mayor o igual a 0.
\(\begin{aligned} 2-x & \geq 0 \\-x & \geq-2 \\ x & \leq 2 \end{aligned}\)
Dominio:\(x \in(-\infty, 2]\)
2. \(y=\frac{3 x}{x^{2}+7 x+12}\)
El denominador no puede ser igual a\(0 .\) Primero encuentra qué valores de lo\(x\) haría igual a cero y luego puedes excluir esos valores.
\(\begin{aligned} x^{2}+7 x+12 &=0 \\(x+4)(x+3) &=0 \\ x &=-4,-3 \end{aligned}\)
Dominio:\(x \in(-\infty,-4) \cup(-4,-3) \cup(-3, \infty)\)
3. \(y=-4 \ln (3 x-9)+11\)
El argumento debe ser estrictamente mayor que 0.
\(3 x-9>0\)
\(3 x>9\)
\(x>3\)
Dominio:\(x \in(3, \infty)\)
¿Cuál es el dominio y el rango de la onda sinusoidal?
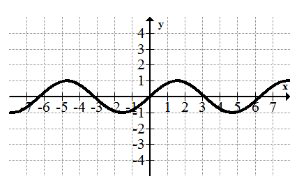
Dominio:\(x \in(-\infty, \infty)\)
Rango:\(y \in[-1,1]\)
Revisar
Convierta las siguientes descripciones de números en notación de intervalo.
1. Todos los números positivos sin incluir 0.
2. Cada número entre -1 y 1 incluyendo -1 pero no 1.
3. Cada número entre 1 y 5 no incluye 2 o 3, pero incluyendo 1 y 5.
4. Cada número mayor a 5, sin incluir 5.
5. Todos los números reales excepto 1.
Traducir las siguientes desigualdades en notación de intervalo.
6. \(-4<x \leq 5\)
7. \(x>0\)
8. \(-\infty<x \leq 4\)o\(5<x<\infty\)
9.
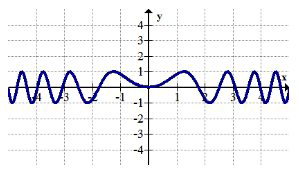
10.
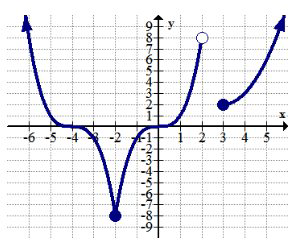
Dado el dominio y el rango establecidos, dibujar una posible gráfica.
11. Dominio:\(x \in[0, \infty)\) Rango:\(y \in(-2,2]\)
12. Dominio:\(x \in[-4,1) \cup(1, \infty)\) Rango:\(y \in(-\infty, \infty)\)
13. Dada la tabla, encuentra el dominio y el rango.
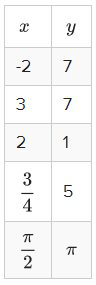
Encuentra el dominio para las siguientes funciones.
14. \(y=-3 \sqrt{x+4}-1\)
\(y=\frac{7}{x+6}-1\)
16. \(y=5 \ln \left(x^{2}-1\right)+4\)

