1.5:1.5 Máximos y Mínimos
- Page ID
- 107344
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al montar una montaña rusa siempre hay un punto que es el más alto absoluto del suelo. Por lo general, hay muchos otros lugares que alcanzan bastante alto, simplemente no tan alto como el primero. También hay lugares donde la montaña rusa se sumerge con una siendo la más baja absoluta a la que puede ir la montaña rusa. ¿Cómo se identifican y distinguen entre estos diferentes picos y valles de una manera precisa?
Encontrar Máximos y Mínimos
Un máximo global se refiere al punto con el mayor\(y\) valor posible en una función. Un mínimo global se refiere al punto con el menor\(y\) valor posible. Juntos estos dos valores se denominan extremos globales. Solo puede haber un máximo global y solo un mínimo global. Global se refiere a todo el espacio donde se define la función. Los extremos globales también se llaman extremos absolutos.
Además de los máximos globales y mínimos globales, también hay máximos locales extremos o relativos y mínimos relativos. Se emplea la palabra relativo porque en relación con algún barrio, estos valores destacan por ser los más altos o los más bajos.
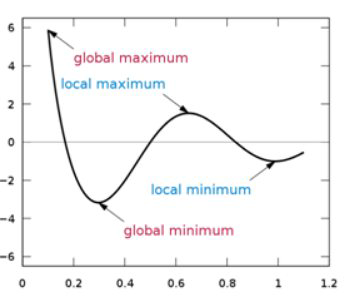
Cálculo utiliza herramientas analíticas avanzadas para calcular valores extremos, pero para los fines de Precálculo es suficiente para poder identificar y categorizar valores extremos gráficamente o mediante el uso de la tecnología. Por ejemplo, el TI-84 tiene un buscador máximo cuando selecciona <2 nd > entonces.
Ejemplos
Anteriormente, se le pidió identificar y distinguir entre diferentes picos y valles en una gráfica. Los máximos y mínimos deben ser intuitivos porque simplemente identifican los puntos más altos y los puntos más bajos, o los picos y los valles, en una gráfica. Existe una distinción formal sobre si un máximo es el más alto en algún intervalo abierto local (no importa cuán pequeño sea), o si es simplemente el más alto en general.
Identificar y categorizar todos los extrema.
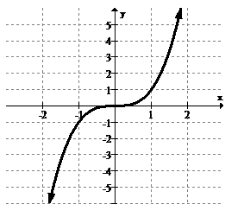
No hay máximos ni mínimos globales o locales. La función se aplana, pero en realidad no alcanza un pico o un valle.
Identifica y categoriza todos los extremos en la siguiente gráfica:
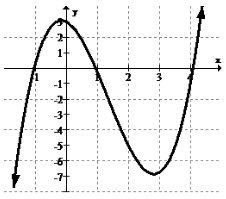
Dado que la función aparece de las flechas para aumentar y disminuir más allá de la visualización, no hay extremos globales. Hay un máximo local en aproximadamente (0, 3) y un mínimo local en aproximadamente (2.8, -7).
Identifica y categoriza todos los extremos en la siguiente gráfica:
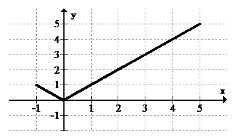
Dado que la función parece terminar abruptamente en los puntos finales y no va más allá de la visualización, los puntos finales son importantes.
Hay un mínimo global en (0, 0). Hay un máximo local en (-1, 1) y un máximo global en (5, 5).
Identifica y categoriza todos los extremos en la siguiente gráfica:
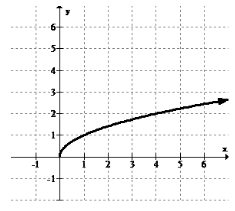
Dado que esta función parece aumentar a la derecha como lo indica la flecha no hay un máximo global. Tampoco hay otros puntos altos, por lo que no hay máximos locales. Solo existe el punto final en (0, 0) que es un mínimo global.
Revisar
Utilice la gráfica a continuación para 1-2.
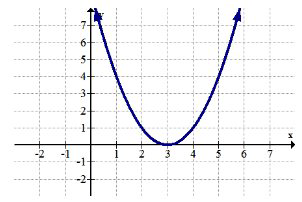
1. Identificar cualquier extrema global.
2. Identificar cualquier extrema local.
Utilice la gráfica de abajo para 3-4.
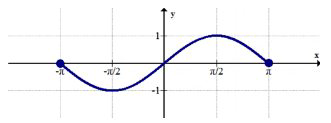
3. Identificar cualquier extrema global.
4. Identificar cualquier extrema local.
Utilice la gráfica de abajo para 5-6.
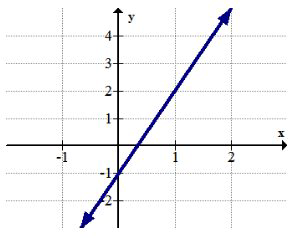
5. Identificar cualquier extrema global.
6. Identificar cualquier extrema local.
Utilice la gráfica de abajo para 7-8.
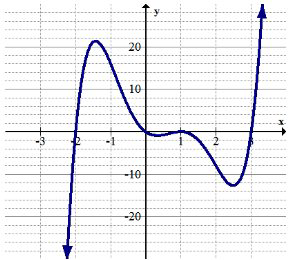
7. Identificar cualquier extrema global.
8. Identificar cualquier extrema local.
Utilice la gráfica de abajo para 9-10.
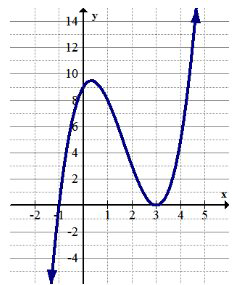
9. Identificar cualquier extrema global.
10. Identificar cualquier extrema local.
11. Explicar la diferencia entre un máximo global y un máximo local.
12. Dibuja un ejemplo de una gráfica con un mínimo global y un máximo local, pero sin un máximo global.
13. Dibuja un ejemplo de una gráfica con máximos y mínimos locales, pero sin extremos globales.
14. Usa tu calculadora gráfica para identificar y categorizar los extremos de:
\(f(x)=\frac{1}{2} x^{4}+2 x^{3}-6.5 x^{2}-20 x+24\)
15. Usa tu calculadora gráfica para identificar y categorizar los extremos de:
\(g(x)=-x^{4}+2 x^{3}+4 x^{2}-2 x-3\)