2.7 Agujeros en Funciones Racionales
- Page ID
- 107408
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En una función como\(f(x)=\frac{(3 x+1)(x-1)}{(x-1)},\) debes tener en cuenta que el factor\((x-1)\) claramente cancela dejando solo\(3 x-1\). Esta parece ser una línea regular. ¿Qué pasa con esta línea en\(x=1\)?
Agujeros y funciones racionales
Un agujero en una gráfica parece un círculo hueco. Representa el hecho de que la función se acerca al punto, pero en realidad no se define sobre ese\(x\) valor preciso.
Echa un vistazo a la gráfica de la siguiente ecuación:
\(f(x)=(2 x+2) \cdot \frac{\left(x+\frac{1}{2}\right)}{\left(x+\frac{1}{2}\right)}\)
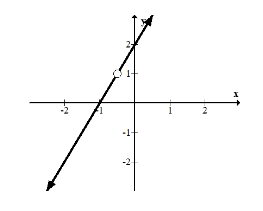
La razón por la que esta función no se define en\(-\frac{1}{2}\)\(-\frac{1}{2}\) es porque no está en el dominio de la función. Como puede ver,\(f\left(-\frac{1}{2}\right)\) está indefinido porque hace que el denominador de la parte racional de la función sea cero lo que hace que toda la función sea indefinida. También nota que una vez que los factores se cancelan/eliminan entonces te quedan con una función normal que en este caso es\(2 x+2\). El agujero en esta situación está en\(\left(-\frac{1}{2}, 1\right)\) porque después de eliminar los factores que cancelan,\(f\left(-\frac{1}{2}\right)=1\)
Esta es la esencia de lidiar con los agujeros en las funciones racionales. Deberías cancelar lo que puedas y graficar la función como normal asegurándote de anotar qué\(x\) valores hacen que la función sea indefinida. Una vez graficada la función sin agujeros retrocede e inserta los círculos huecos indicando qué\(x\) valores se eliminan del dominio. Es por ello que a los agujeros se les llama discontinuidades removibles.
Mire la primera parte de este video y concéntrese en los agujeros en las ecuaciones racionales.
Ejemplos
Anteriormente, se le preguntó qué pasa con la ecuación\(f(x)=\frac{(3 x+1)(x-1)}{(x-1)}\) at\(x=1\). ya que esta función que no se define en\(x=1\) hay una discontinuidad removible que se representa como un círculo hueco en la gráfica. De lo contrario la función se comporta precisamente como\(3 x+1\).
Grafique la siguiente función racional e identifique las discontinuidades removibles.
\(f(x)=\frac{-x^{3}+3 x^{2}+2 x-4}{x-1}\)
Esta función requiere algo de álgebra para cambiarla de manera que los factores removibles se hagan evidentes. Debes sospechar que\((x-1)\) es un factor del numerador e intentar polinomio o división sintética a factorizar. Cuando lo haces, la función se convierte en:
\(f(x)=\frac{\left(-x^{2}+2 x+4\right)(x-1)}{(x-1)}\)

La discontinuidad removible ocurre en (1, 5).
Grafique la siguiente función racional e identifique las discontinuidades removibles.
\(f(x)=\frac{x^{6}-6 x^{5}+5 x^{4}+27 x^{3}-48 x^{2}-9 x+54}{x^{3}-7 x-6}\)
Esta es probablemente una de las expresiones racionales más desafiantes con solo agujeros que la gente intenta graficar a mano. Hay múltiples formas de comenzar, pero un buen hábito en el que entrar es factorizar todo lo que puedas inicialmente. El denominador parece menos complicado con posibles factores\((x \pm 1),(x \pm 2),(x \pm 3),(x \pm 6) .\) Usando la división polinómica, encontrarás que el denominador se convierte en:
\(f(x)=\frac{x^{6}-6 x^{5}+5 x^{4}+27 x^{3}-48 x^{2}-9 x+54}{(x+1)(x+2)(x-3)}\)
Los factores del denominador son fuertes indicios en cuanto a los factores del numerador así que usa la división polinómica y prueba cada uno. Cuando factorizas completamente el numerador tendrás:
\(f(x)=\frac{\left(x^{3}-6 x^{2}+12 x-9\right)(x+1)(x+2)(x-3)}{(x+1)(x+2)(x-3)}\)
Anote los factores que cancelan\((x=-1,-2,3)\) y luego trabajan con la función cúbica que queda.
\(f(x)=x^{3}-6 x^{2}+12 x-9\)
En este punto probablemente sea razonable hacer una tabla y trazar puntos para tener una idea de dónde vive esta función cúbica. También podrías notar que los coeficientes son casi del patrón 1 3 3 1 que es la expansión binomial. Al separar el -9 en -8 -1 se pueden factorizar los primeros cuatro términos.
\(f(x)=x^{3}-6 x^{2}+12 x-8-1=(x-2)^{3}-1\)
Esta es una función cúbica que ha sido desplazada a la derecha por dos unidades y una unidad hacia abajo.
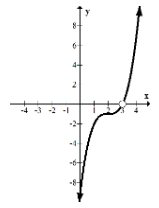
Tenga en cuenta que hay dos agujeros que no caben en la ventana gráfica. Cuando esto sucede, aún necesita anotar dónde aparecerían dada una ventana del tamaño adecuado. Para ello, sustituya los\(x\) valores inválidos:\(x=-1,-2,3\) en el cúbico factorizado que quedó después de cancelar.
f (x) = (x-2) ^ {3} -1
Agujeros: (3, 0); (-1, -28); (-2, -65)
Sin graficar, identificar la ubicación de los agujeros de la siguiente función.
\(f(x)=\frac{x^{3}+4 x^{2}+x-6}{x^{2}+5 x+6}\)
Primer factor todo. Después, identifique los\(x\) valores que hacen que el denominador sea cero y use esos valores para encontrar la ubicación exacta de los agujeros.
\(f(x)=\frac{(x+2)(x+3)(x-1)}{(x+3)(x+2)}\)
Agujeros: (-3, -4); (-2, -3)
¿Cuál es una ecuación posible para la siguiente función racional?
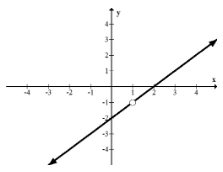
La función parece ser una línea con una discontinuidad removible en\((1,-1) .\) La línea es tiene pendiente 1 y\(y\) -intercepción de -2 y así tiene la ecuación:
\(f(x)=x-2\)
La discontinuidad removible no debe permitir que el\(x\) sea 1 lo que implica que es de la forma\(\frac{x-1}{x-1}\). Por lo tanto, la función es:
\(f(x)=\frac{(x-2)(x-1)}{x-1}\)
Revisar
1. ¿Cómo encuentras los agujeros de una función racional?
2. ¿Cuál es la diferencia entre un agujero y una discontinuidad removible?
3. Si ves un círculo hueco en una gráfica, ¿qué significa eso?
Sin graficar, identificar la ubicación de los agujeros de las siguientes funciones.
4. \(f(x)=\frac{x^{2}+3 x-4}{x-1}\)
5. \(g(x)=\frac{x^{2}+8 x+15}{x+3}\)
6. \(h(x)=\frac{x^{3}+6 x^{2}+2 x-8}{x^{2}+x-2}\)
7. \(k(x)=\frac{x^{3}+6 x^{2}+2 x-8}{x^{2}-3 x+2}\)
8. \(j(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}-9}\)
9. \(f(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}-5 x+4}\)
10. \(g(x)=\frac{x^{3}-4 x^{2}-19 x-14}{x^{2}-8 x+7}\)
11. ¿Cuál es una ecuación posible para la siguiente función racional?

12. ¿Cuál es una ecuación posible para la siguiente función racional?

Esbozar las siguientes funciones racionales.
13. \(f(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}-x-12}\)
14. \(g(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}+8 x+15}\)
15. \(h(x)=\frac{x^{3}-4 x^{2}-19 x-14}{x^{2}-6 x-7}\)

