6.5: Ecuaciones Trigonométricas
- Page ID
- 107167
Resolver una ecuación trigonométrica es como resolver una ecuación regular. Utilizarás factorización y otras técnicas algebraicas para obtener la variable en un lado. La mayor diferencia con las ecuaciones trigonométricas es la oportunidad de que haya un número infinito de soluciones que deben describirse con un patrón. La ecuación\(\cos x=1\) tiene muchas soluciones entre ellas 0 y\(2 \pi .\) ¿Cómo las describirías a todas?
Resolviendo Ecuaciones Trigonométricas
Las identidades que has aprendido son útiles para resolver ecuaciones trigonométricas. El objetivo de resolver una ecuación no ha cambiado. Haz lo que sea necesario para obtener la variable sola en un lado de la ecuación. Factorizar, especialmente con la identidad pitagórica, es crítico.
Trate de dar respuestas exactas (no redondeadas) al resolver ecuaciones trigonométricas. Si está trabajando con una calculadora, tenga en cuenta que si bien algunas calculadoras más nuevas pueden proporcionar respuestas exactas como la\(\frac{\sqrt{3}}{2}\) mayoría de las calculadoras producirán un decimal de\(0.866 \ldots\) Si ve un decimal como\(0.866 \ldots,\) intente cuadrarlo. El resultado podría ser una buena fracción como\(\frac{3}{4}\). Entonces se puede concluir lógicamente que el decimal original debe ser la raíz cuadrada de\(\frac{3}{4}\) o\(\frac{\sqrt{3}}{2}\)
Al resolver, si los dos lados de la ecuación son siempre iguales, entonces la ecuación es una identidad. Si los dos lados de una ecuación nunca son iguales, como con\(\sin x=3\), entonces la ecuación no tiene solución.
Ejemplos
Anteriormente, se le preguntó cómo podría describir las muchas soluciones de\(\cos x=1\). Cuando escribes\(\cos ^{-1} 1\) en tu calculadora, producirá solo una solución que es\(0 .\) Para describir todas las soluciones debes usar la lógica y la gráfica para averiguar que el coseno también tiene una altura de 1 en\(-2 \pi, 2 \pi,-4 \pi, 4 \pi \ldots\) Afortunadamente todos estos valores son secuencias en un patrón claro para que puedas describir todos ellos en general con la siguiente notación:
\(x=0 \pm n \cdot 2 \pi\)donde\(n\) es un entero, o\(x=\pm n \cdot 2 \pi\) donde\(n\) es un entero.
Resolver algebraicamente la siguiente ecuación y confirmar gráficamente en el intervalo\([-2 \pi, 2 \pi]\).
\(\cos 2 x=\sin x\)
\(\begin{aligned} \cos 2 x &=\sin x \\ 1-2 \sin ^{2} x &=\sin x \\ 0 &=2 \sin ^{2} x+\sin x-1 \\ 0 &=(2 \sin x-1)(\sin x+1) \end{aligned}\)
Resolver el primer conjunto de partes igual a cero dentro del intervalo produce:
\(\begin{aligned} 0 &=2 \sin x-1 \\ \frac{1}{2} &=\sin x \\ x &=\frac{\pi}{6}, \frac{5 \pi}{6},-\frac{11 \pi}{6},-\frac{7 \pi}{6} \end{aligned}\)
Resolviendo el segundo conjunto de partes iguales a cero rendimientos:
\(\begin{aligned} 0 &=\sin x+1 \\-1 &=\sin x \\ x &=-\frac{\pi}{2}, \frac{3 \pi}{2} \end{aligned}\)
Estas son las seis soluciones que aparecerán como intersecciones de las dos gráficas\(f(x)=\cos 2 x\) y\(g(x)=\sin x\)
Determinar la solución general a la siguiente ecuación.
\(\cot x-1=0\)
\(\cot x-1=0\)
\(\cot x=1\)
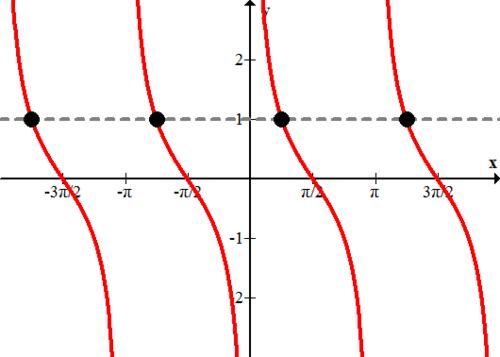
Una solución es\(x=\frac{\pi}{4} .\) Sin embargo, dado que esta pregunta pide la solución general, es necesario encontrar todas las soluciones posibles. Tienes que saber que la cotangente tiene un periodo de\(\pi\) lo que significa que si sumas o restas a\(\pi\) partir de\(\frac{\pi}{4}\) entonces también producirá una altura de\(1 .\) Para capturar todos estos otros\(x\) valores posibles debes usar esta notación.
\(x=\frac{\pi}{4} \pm n \cdot \pi\)donde\(n\) es un entero
Observe que las ecuaciones trigonométricas pueden tener un número infinito de soluciones que se repiten en cierto patrón porque son funciones periódicas. Cuando veas estas indicaciones recuerda encontrar todas las soluciones usando notación como en este ejemplo.
Resuelve la siguiente ecuación.
\(4 \cos ^{2} x-1=3-4 \sin ^{2} x\)
\(\begin{aligned} 4 \cos ^{2} x-1 &=3-4 \sin ^{2} x \\ 4 \cos ^{2} x+4 \sin ^{2} x &=3+1 \\ 4\left(\cos ^{2} x+\sin ^{2} x\right) &=4 \\ 4 &=4 \end{aligned}\)
Esta ecuación siempre es cierta lo que significa que el lado derecho es siempre igual al lado izquierdo. Esta es una identidad.
Resuelve exactamente la siguiente ecuación.
\(2 \cos ^{2} x+3 \cos x-2=0\)
Tenga en cuenta\(\cos x \neq-2\) que lo que significa que solo se necesita resolver una ecuación para las soluciones.
\(\begin{aligned} 2 \cos x-1 &=0 \\ \cos x &=\frac{1}{2} \\ x &=\frac{\pi}{3},-\frac{\pi}{3} \end{aligned}\)
Estas son las soluciones dentro del intervalo\(-\pi\) a\(\pi .\) ya que esto representa un periodo completo de coseno, el resto de las soluciones son solo múltiplos de\(2 \pi\) sumado y restado a estos dos valores.
\(x=\pm \frac{\pi}{3} \pm n \cdot 2 \pi\)donde\(n\) es un entero
Revisar
Resuelve cada ecuación en el intervalo\([0,2 \pi)\).
1. \(3 \cos ^{2} \frac{x}{2}=3\)
2. \(4 \sin ^{2} x=8 \sin ^{2} \frac{x}{2}\)
Encuentra soluciones aproximadas para cada ecuación en el intervalo\([0,2 \pi)\)
3. \(3 \cos ^{2} x+10 \cos x+2=0\)
4. \(\sin ^{2} x+3 \sin x=5\)
5. \(\cdot \tan ^{2} x+\tan x=3\)
6. \(\cot ^{2} x+5 \tan x+14=0\)
7. \(\sin ^{2} x+\cos ^{2} x=1\)
Resuelve cada ecuación en el intervalo\(\left[0,360^{\circ}\right)\).
8. \(2 \sin \left(x-\frac{\pi}{2}\right)=1\)
9. \(4 \cos (x-\pi)=4\)
Resolver cada ecuación en el intervalo\([2 \pi, 4 \pi)\)
10. \(\cos ^{2} x+2 \cos x+1=0\)
11. \(3 \sin x=2 \cos ^{2} x\)
12. \(\tan x \sin ^{2} x=\tan x\)
13. \(\sin ^{2} x+1=2 \sin x\)
14. \(\sec ^{2} x=4\)
15. \(\sin ^{2} x-4=\cos ^{2} x-\cos 2 x-4\)