4.6: Distribución hipergeométrica
- Page ID
- 153161
La distribución hipergeométrica surge cuando uno toma muestras de una población finita, haciendo que los ensayos dependan unos de otros. Hay cinco características de un experimento hipergeométrico.
Características de un experimento hipergeométrico
- Se toman muestras de dos grupos.
- A usted le preocupa un grupo de interés, llamado el primer grupo.
- Muestrea sin reemplazo de los grupos combinados. Por ejemplo, quieres elegir un equipo de softbol de un grupo combinado de 11 hombres y 13 mujeres. El equipo está formado por diez jugadores.
- Cada pico no es independiente, ya que el muestreo es sin reemplazo. En el ejemplo del softbol, la probabilidad de escoger primero a una mujer es\(\frac{13}{24}\). La probabilidad de elegir a un hombre en segundo lugar es\(\frac{11}{23}\) si una mujer fue escogida primero. Es\(\frac{10}{23}\) si un hombre fue escogido primero. La probabilidad del segundo pick depende de lo ocurrido en el primer pick.
- No se trata de Juicios de Bernoulli.
Los resultados de un experimento hipergeométrico se ajustan a una distribución de probabilidad hipergeométrica. La variable aleatoria\(X\) = el número de ítems del grupo de interés.
Ejemplo\(\PageIndex{1}\)
Un plato de dulces contiene 100 gominollos y 80 gomitas. Cincuenta caramelos se recogen al azar. ¿Cuál es la probabilidad de que 35 de las 50 sean gomitas? Los dos grupos son las gominollas y las gomitas. Dado que la pregunta de probabilidad pide la probabilidad de recoger gomitas, el grupo de interés (primer grupo) son las gomitas. El tamaño del grupo de interés (primer grupo) es de 80. El tamaño del segundo grupo es de 100. El tamaño de la muestra es de 50 (gomitas o gomitas). Dejar\(X =\) el número de gomitas en la muestra de 50. \(X\)adquiere los valores\(x = 0, 1, 2, ..., 50\). ¿Cuál es la declaración de probabilidad escrita matemáticamente?
Responder
\(P(x = 35)\)
Ejercicio\(\PageIndex{1}\)
Una bolsa contiene azulejos de letras. Cuarenta y cuatro de las fichas son vocales, y 56 son consonantes. Siete fichas se recogen al azar. Quieres saber la probabilidad de que cuatro de los siete mosaicos sean vocales. ¿Cuál es el grupo de interés, el tamaño del grupo de interés y el tamaño de la muestra?
- Responder
-
El grupo de interés son los mosaicos de letras vocales. El tamaño del grupo de interés es 44. El tamaño de la muestra es de siete.
Ejemplo\(\PageIndex{2}\)
Supongamos que se sabe que un envío de 100 reproductores de DVD tiene diez reproductores defectuosos. Un inspector elige al azar 12 para su inspección. Le interesa determinar la probabilidad de que, entre los 12 jugadores, a lo sumo dos sean defectuosos. Los dos grupos son los 90 reproductores de DVD no defectuosos y los 10 reproductores de DVD defectuosos. El grupo de interés (primer grupo) es el grupo defectuoso porque la pregunta de probabilidad pide la probabilidad de que como máximo dos reproductores de DVD defectuosos sean como máximo. El tamaño de la muestra es de 12 reproductores de DVD. (Pueden ser no defectuosos o defectuosos.) Dejar que\(X =\) el número de reproductores DVD defectuosos en la muestra de 12. \(X\)adquiere los valores\(0, 1, 2, \dotsc, 10\). \(X\)no podrá asumir los valores 11 o 12. El tamaño de la muestra es 12, pero solo hay 10 reproductores de DVD defectuosos. Escribir matemáticamente la declaración de probabilidad.
Responder
\(P(x \leq 2)\)
Ejercicio\(\PageIndex{2}\)
Un bruto de huevos contiene 144 huevos. Se sabe que un bruto particular tiene 12 huevos agrietados. Un inspector elige al azar 15 para su inspección. Ella quiere saber la probabilidad de que, entre los 15, a lo sumo tres estén agrietados. ¿Qué es\(X\) y qué valores adquiere?
- Responder
-
Dejar\(X =\) el número de huevos agrietados en la muestra de 15. \(X\)adquiere los valores\(0, 1, 2, \dotsc, 12\).
Ejemplo\(\PageIndex{3}\)
Eres presidente de una organización de eventos especiales en el campus. Se necesita un comité de siete alumnos para planear una fiesta especial de cumpleaños para el presidente del colegio. Su organización está integrada por 18 mujeres y 15 hombres. Te interesa el número de hombres en tu comisión. Si los integrantes del comité son seleccionados al azar, ¿cuál es la probabilidad de que su comité tenga más de cuatro hombres?
Se trata de un problema hipergeométrico porque estás eligiendo a tu comité entre dos grupos (hombres y mujeres).
- ¿Estás eligiendo con o sin reemplazo?
- ¿Cuál es el grupo de interés?
- ¿Cuántos hay en el grupo de interés?
- ¿Cuántos hay en el otro grupo?
- Vamos\(X =\) _________ en la comisión. ¿Qué\(X\) valores adquiere?
- La pregunta de probabilidad es\(P(\) _______\()\).
Solución
- sin
- los hombres
- 15 hombres
- 18 mujeres
- Que\(X =\) el número de hombres en el comité. \(x = 0, 1, 2, \dotsc, 7\).
- \(P(x > 4)\)
Ejercicio\(\PageIndex{3}\)
Una paleta tiene 200 cajas de leche. De los 200 cartones, se sabe que diez de ellos se han filtrado y no se pueden vender. Un empleado de stock elige al azar 18 para su inspección. Quiere saber la probabilidad de que entre los 18, no más de dos estén goteando. Dar cinco razones por las que se trata de un problema hipergeométrico.
- Responder
-
- Hay dos grupos.
- Te preocupa un grupo de interés.
- Muestrea sin reemplazo.
- Cada pick no es independiente.
- No se trata de Juicios de Bernoulli.
Notación para el Hipergeométrico:\(H =\) Hypergeometric Probability Distribution Function
\[X \sim H(r, b, n)\]
Lee esto como "\(X\)es una variable aleatoria con una distribución hipergeométrica”. Los parámetros son\(r, b\), y\(n\);\(r =\) el tamaño del grupo de interés (primer grupo),\(b =\) el tamaño del segundo grupo,\(n =\) el tamaño de la muestra elegida.
Ejemplo\(\PageIndex{4}\)
Un comité de sitio escolar se elegirá al azar entre seis hombres y cinco mujeres. Si el comité consta de cuatro miembros elegidos al azar, ¿cuál es la probabilidad de que dos de ellos sean hombres? ¿Cuántos hombres espera estar en el comité?
Vamos\(X\) = el número de hombres en el comité de cuatro. Los hombres son el grupo de interés (primer grupo).
\(X\)adquiere los valores\(0, 1, 2, 3, 4\), dónde\(r = 6, b = 5\), y\(n = 4\). \(X \sim H(6, 5, 4)\)
Encontrar\(P(x = 2)\). \(P(x = 2) = 0.4545\)(calculadora o computadora)
Actualmente, el TI-83+ y el TI-84 no tienen funciones de probabilidad hipergeométrica. Hay una serie de paquetes informáticos, incluyendo Microsoft Excel, que sí.
La probabilidad de que haya dos hombres en el comité es de aproximadamente 0.45.
La gráfica de\(X \sim H(6, 5, 4)\) es:
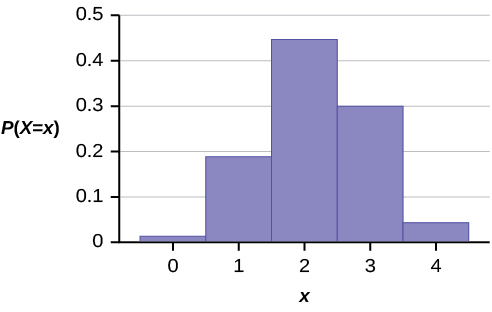
El eje y contiene la probabilidad de\(X\), donde\(X =\) el número de hombres en el comité.
Se esperaría\(m = 2.18\) (alrededor de dos) hombres en el comité.
La fórmula para la media es
\[\mu = \frac{nr}{r+b} \frac{(4)(6)}{6+5} = 2.18\]
Ejercicio\(\PageIndex{4}\)
Un equipo intramural de basquetbol se elegirá al azar entre 15 niños y 12 niñas. El equipo cuenta con diez ranuras. Quieres saber la probabilidad de que ocho de los jugadores sean chicos. ¿Cuál es el grupo de interés y la muestra?
- Responder
-
El grupo de interés son los 15 chicos. La muestra consta de las diez ranuras del equipo intramural de basquetbol.
Resumen
Un experimento hipergeométrico es un experimento estadístico con las siguientes propiedades:
- Se toman muestras de dos grupos.
- A usted le preocupa un grupo de interés, llamado el primer grupo.
- Muestreo sin reemplazo de los grupos combinados.
- Cada pico no es independiente, ya que el muestreo es sin reemplazo.
- No se trata de Juicios de Bernoulli.
Los resultados de un experimento hipergeométrico se ajustan a una distribución de probabilidad hipergeométrica. La variable aleatoria\(X\) = el número de ítems del grupo de interés. \(X\)Se denota la distribución de\(X \sim H(r, b, n)\), donde se indica\(r =\) el tamaño del grupo de interés (primer grupo),\(b =\) el tamaño del segundo grupo y\(n =\) el tamaño de la muestra elegida. De ello se deduce que\(n \leq r + b\). La media de\(X\) es\(\mu = \frac{nr}{r+b}\) y la desviación estándar es\(\sigma = \sqrt{\frac{rbn(r+b-n)}{(r+b)^{2}(r+b-1)}}\).
Revisión de Fórmula
\(X \sim H(r, b, n)\)significa que la variable aleatoria discreta\(X\) tiene una distribución de probabilidad hipergeométrica con\(r =\) el tamaño del grupo de interés (primer grupo),\(b =\) el tamaño del segundo grupo y\(n =\) el tamaño de la muestra elegida.
\(X\)= el número de ítems del grupo de interés que se encuentran en la muestra elegida, y\(X\) pueden tomar los valores\(x = 0, 1, \dotsc,\) hasta el tamaño del grupo de interés. (El valor mínimo para\(X\) puede ser mayor que cero en algunos casos.)
\(n \leq r + b\)
La media de\(X\) viene dada por la fórmula\(\mu = \frac{nr}{r+b}\) y la desviación estándar es\(= \sqrt{\frac{rbn(r+b-n)}{(r+b)^{2}(r+b-1)}}\).
Utilice la siguiente información para responder a los siguientes cinco ejercicios: Supongamos que un grupo de estudiantes de estadística se divide en dos grupos: carreras de negocios y carreras no empresariales. Hay 16 carreras empresariales en el grupo y siete carreras no comerciales en el grupo. Se toma una muestra aleatoria de nueve alumnos. Nos interesa el número de carreras empresariales en la muestra.
Ejercicio\(\PageIndex{5}\)
En palabras, defina la variable aleatoria\(X\).
Responder
\(X =\)el número de carreras de negocios en la muestra.
Ejercicio\(\PageIndex{6}\)
\(X \sim\)_____ (_____, _____)
Ejercicio\(\PageIndex{7}\)
¿Qué\(X\) valores adquiere?
Responder
\(2, 3, 4, 5, 6, 7, 8, 9\)
Ejercicio\(\PageIndex{8}\)
Encuentra la desviación estándar.
Ejercicio\(\PageIndex{9}\)
En promedio (\(\mu\)), ¿cuántos esperarías que fueran carreras de negocios?
Responder
6.26
Glosario
- Experimento Hipergeométrico
- un experimento estadístico con las siguientes propiedades:
- Se toman muestras de dos grupos.
- A usted le preocupa un grupo de interés, llamado el primer grupo.
- Muestreo sin reemplazo de los grupos combinados.
- Cada pico no es independiente, ya que el muestreo es sin reemplazo.
- No se trata de Juicios de Bernoulli.
- Probabilidad Hipergeométrica
- una variable aleatoria discreta (RV) que se caracteriza por:
- Un número fijo de juicios.
- La probabilidad de éxito no es la misma de un juicio a otro.


