9.6: Información adicional y ejemplos completos de prueba de hipótesis

Última actualización
Guardar como PDF

Page ID: 153372

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En un problema de prueba de hipótesis, es posible que veas palabras como “el nivel de significancia es del 1%”. El "1%" es el preconcebido o preestablecido$\alpha$.
El estadístico que configura la prueba de hipótesis selecciona el valor de α a usar antes de recolectar los datos de la muestra.
Si no se da ningún nivel de significancia, un estándar común a usar es$\alpha = 0.05$.
Cuando calculas el$p$ -value y dibujas la imagen, el$p$ -value es el área en la cola izquierda, la cola derecha, o se divide uniformemente entre las dos colas. Por esta razón, llamamos a la prueba de hipótesis izquierda, derecha o de dos colas.
La hipótesis alternativa,$H_{a}$, te dice si la prueba es izquierda, derecha, o de dos colas. Es la clave para realizar la prueba apropiada.
$H_{a}$nunca tiene un símbolo que contenga un signo igual.
Pensando en el significado del$p$ -valor: Un analista de datos (y cualquier otra persona) debería tener más confianza en que tomó la decisión correcta de rechazar la hipótesis nula con un$p$ valor -menor (por ejemplo, 0.001 en contraposición a 0.04) incluso si usaba el nivel 0.05 para alfa. De igual manera, para un gran valor p como 0.4, a diferencia de un$p$ valor -de 0.056 ($\alpha = 0.05$es menor que cualquiera de los dos números), una analista de datos debería tener más confianza en que tomó la decisión correcta al no rechazar la hipótesis nula. Esto hace que el analista de datos use el juicio en lugar de aplicar reglas sin pensar.

Los siguientes ejemplos ilustran una prueba de izquierda, derecha y dos colas.

Ejemplo$\PageIndex{1}$

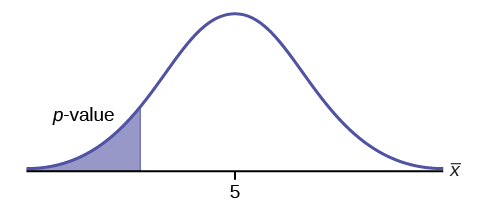
$H_{0}: \mu = 5, H_{a}: \mu < 5$

Prueba de media de una sola población. $H_{a}$te dice que la prueba es de cola izquierda. La imagen del$p$ valor -es la siguiente:

Curva de distribución normal de una sola media poblacional con un valor de 5 en el eje x y el valor p apunta al área de la cola izquierda de la curva. — Figura$\PageIndex{1}$

Ejercicio$\PageIndex{1}$

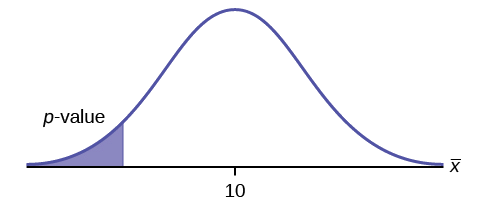
$H_{0}: \mu = 10, H_{a}: \mu < 10$

Supongamos que el$p$ valor -es 0.0935. ¿Qué tipo de prueba es esta? Dibuja la imagen del$p$ -valor.

Contestar

prueba de cola izquierda

Ejemplo$\PageIndex{2}$

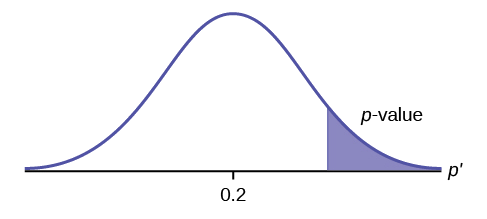
$H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2$

Esta es una prueba de una sola proporción poblacional. $H_{a}$te dice que la prueba es de cola derecha. La imagen del valor p es la siguiente:

Curva de distribución normal de una sola proporción poblacional con el valor de 0.2 en el eje x. El valor p apunta al área en la cola derecha de la curva. — Figura$\PageIndex{3}$

Ejercicio$\PageIndex{2}$

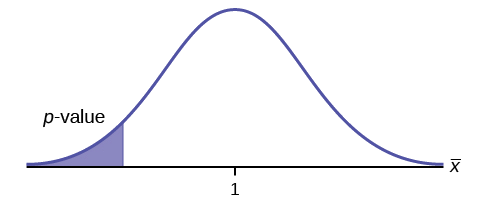
$H_{0}: \mu \leq 1, H_{a}: \mu > 1$

Supongamos que el$p$ valor -es 0.1243. ¿Qué tipo de prueba es esta? Dibuja la imagen del$p$ -valor.

Contestar

prueba de cola derecha

Ejemplo$\PageIndex{3}$

$H_{0}: \mu = 50, H_{a}: \mu \neq 50$

Esta es una prueba de media de una sola población. $H_{a}$te dice que la prueba es de dos colas. La imagen del$p$ valor -es la siguiente.

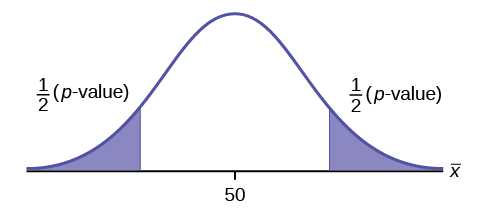
Curva de distribución normal de una sola población media con un valor de 50 en el eje x. Se muestran las fórmulas de valor p, 1/2 (valor p), para una prueba de dos colas para las áreas en las colas izquierda y derecha de la curva. — Figura$\PageIndex{5}$

Ejercicio$\PageIndex{3}$

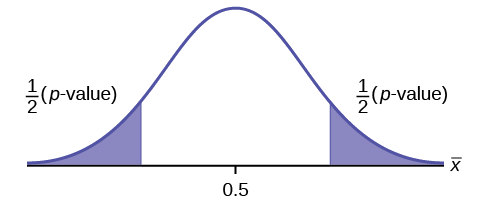
$H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5$

Supongamos que el valor p es 0.2564. ¿Qué tipo de prueba es esta? Dibuja la imagen del$p$ -valor.

Contestar

prueba de dos colas

Ejemplos completos de prueba de hipótesis

Ejemplo$\PageIndex{4}$

Jeffrey, de ocho años de edad, estableció un tiempo medio de 16.43 segundos para nadar el estilo libre de 25 yardas, con una desviación estándar de 0.8 segundos. Su papá, Frank, pensó que Jeffrey podría nadar el estilo libre de 25 yardas más rápido usando gafas. Frank le compró a Jeffrey un nuevo par de gafas caras y cronometró a Jeffrey para 15 nadadas estilo libre de 25 yardas. Para los 15 nadados, el tiempo medio de Jeffrey fue de 16 segundos. Frank pensó que las gafas ayudaron a Jeffrey a nadar más rápido que los 16.43 segundos. Realizar una prueba de hipótesis usando un preestablecido α = 0.05. Supongamos que los tiempos de natación para el estilo libre de 25 yardas son normales.

Contestar

Configurar la Prueba de Hipótesis:

Dado que el problema se trata de una media, se trata de una prueba de una sola media poblacional.

$H_{0}: \mu = 16.43, H_{a}: \mu < 16.43$

Para que Jeffrey nade más rápido, su tiempo será inferior a 16.43 segundos. El "$<$" te dice que esto es de cola izquierda.

Determinar la distribución necesaria:

Variable aleatoria:$\bar{X} =$ el tiempo medio para nadar el estilo libre de 25 yardas.

Distribución para la prueba:$\bar{X}$ es normal (se conoce la desviación estándar de la población:$\sigma = 0.8$)

$\bar{X} - N \left(\mu, \frac{\sigma_{x}}{\sqrt{n}}\right)$Por lo tanto,$\bar{X} - N\left(16.43, \frac{0.8}{\sqrt{15}}\right)$

$\mu = 16.43$proviene$H_{0}$ y no de los datos. $\sigma = 0.8$, y$n = 15$.

Calcular el$p-\text{value}$ usando la distribución normal para una media:

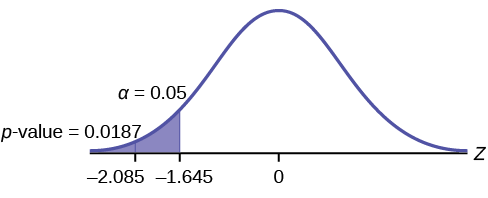
$p\text{-value} = P(\bar{x} < 16) = 0.0187$donde la media muestral en el problema se da como 16.

$p\text{-value} = 0.0187$(Esto se llama el nivel real de significación.) $p-\text{value}$El área a la izquierda de la muestra media se da como 16.

Gráfica:

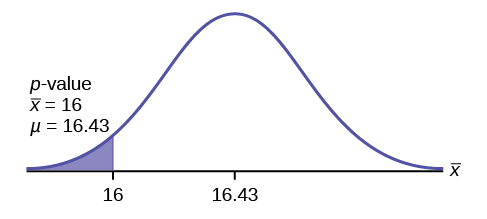
Curva de distribución normal para el tiempo promedio para nadar el estilo libre de 25 yardas con valores 16, como media muestral, y 16.43 en el eje x. Una línea vertical ascendente se extiende desde 16 en el eje x hasta la curva. Una flecha apunta a la cola izquierda de la curva. — Figura$\PageIndex{7}$

$\mu = 16.43$viene de$H_{0}$. Nuestra suposición es$\mu = 16.43$.

Interpretación del$p-\text{value}$: Si$H_{0}$ es cierto, existe una probabilidad de 0.0187 (1.87%) de que el tiempo medio de Jeffrey para nadar el estilo libre de 25 yardas sea de 16 segundos o menos. Debido a que una probabilidad de 1.87% es pequeña, es poco probable que el tiempo medio de 16 segundos o menos haya ocurrido al azar. Es un evento raro.

Comparar$\alpha$ y el$p-\text{value}$:

$\alpha = 0.05 p\text{-value} = 0.0187 \alpha > p\text{-value}$

Tomar una decisión: Desde$\alpha > p\text{-value}$, rechazar$H_{0}$.

Esto quiere decir que rechazas$\mu = 16.43$. En otras palabras, no crees que Jeffrey nade el estilo libre de 25 yardas en 16.43 segundos pero más rápido con las nuevas gafas.

Conclusión: Al nivel de significancia del 5%, concluimos que Jeffrey nada más rápido usando las nuevas gafas. Los datos de la muestra muestran que hay evidencia suficiente de que el tiempo medio de Jeffrey para nadar el estilo libre de 25 yardas es menor a 16.43 segundos.

El valor p se puede calcular fácilmente.

Presiona STAT y flecha hacia PRUEBAS. Presione 1:Z-Test. Flecha la flecha hacia Stats y presiona ENTRAR. Flecha hacia abajo e ingresa 16.43 para$\mu_{0}$ (hipótesis nula), .8 para σ, 16 para la media muestral y 15 para n. Flecha hacia abajo a$\mu$: (hipótesis alternativa) y flecha sobre a$< \mu_{0}$. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. La calculadora no solo calcula el valor p ($p = 0.0187$) sino que también calcula el estadístico de prueba (z -score) para la media de la muestra. $\mu < 16.43$es la hipótesis alternativa. Vuelva a hacer este conjunto de instrucciones excepto la flecha para Dibujar (en lugar de Calcular). Presione ENTER. Aparece una gráfica sombreada con$z = -2.08$ (estadística de prueba) y$p = 0.0187$ ($p-\text{value}$). Asegúrate de que al usar Dibujar no se resalten otras ecuaciones$Y =$ y que las gráficas estén desactivadas.

Cuando la calculadora hace un$Z$ -Test, la función Z-Test encuentra el valor p haciendo un cálculo de probabilidad normal usando el teorema del límite central:

$P(\bar{X} < 16)$2do DISTR.C/normcdf ($(−10^{99},16,16.43,\frac{0.8}{\sqrt{15}})$.

Los errores Tipo I y Tipo II para este problema son los siguientes:

El error Tipo I es concluir que Jeffrey nada el estilo libre de 25 yardas, en promedio, en menos de 16.43 segundos cuando, de hecho, en realidad nada el estilo libre de 25 yardas, en promedio, en 16.43 segundos. (Rechazar la hipótesis nula cuando la hipótesis nula es verdadera.)

El error Tipo II es que no hay evidencia para concluir que Jeffrey nada el estilo libre de 25 yardas, en promedio, en menos de 16.43 segundos cuando, de hecho, en realidad sí nada al estilo libre de 25 yardas, en promedio, en menos de 16.43 segundos. (No rechace la hipótesis nula cuando la hipótesis nula sea falsa).

Ejercicio$\PageIndex{4}$

La distancia media de lanzamiento de una pelota de fútbol para un Marco, un mariscal de campo de primer año de secundaria, es de 40 yardas, con una desviación estándar de dos yardas. El técnico del equipo le dice a Marco que ajuste su agarre para conseguir más distancia. El entrenador registra las distancias para 20 lanzamientos. Para los 20 lanzamientos, la distancia media de Marco fue de 45 yardas. El entrenador pensó que el diferente agarre ayudó a Marco a lanzar más de 40 yardas. Realizar una prueba de hipótesis utilizando un preset$\alpha = 0.05$. Supongamos que las distancias de lanzamiento para balones de fútbol son normales

Primero, determina qué tipo de prueba es esta, configura la prueba de hipótesis, encuentra el valor p, dibuja la gráfica y expone tu conclusión.

Presiona STAT y flecha hacia PRUEBAS. Presione 1:$Z$ -Prueba. Flecha la flecha hacia Stats y presiona ENTRAR. Flecha hacia abajo e ingresa 40 para$\mu_{0}$ (hipótesis nula), 2 para$\sigma$, 45 para la media de la muestra y 20 para$n$. Flecha hacia abajo a$\mu$: (hipótesis alternativa) y establecerla ya sea como$<$,$\neq$, o$>$. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. La calculadora no solo calcula el valor p, sino que también calcula el estadístico de prueba (puntaje z) para la media de la muestra. Seleccionar$<$,$\neq$, o$>$ para la hipótesis alternativa. Vuelva a hacer este conjunto de instrucciones excepto la flecha para Dibujar (en lugar de Calcular). Presione ENTER. Aparece una gráfica sombreada con estadística de prueba y$p$ -valor. Asegúrate de que al usar Dibujar no se resalten otras ecuaciones$Y =$ y que las gráficas estén desactivadas.

Contestar

Dado que el problema se trata de una media, se trata de una prueba de una sola media poblacional.

$H_{0}: \mu = 40$
$H_{a}: \mu > 40$
$p = 0.0062$

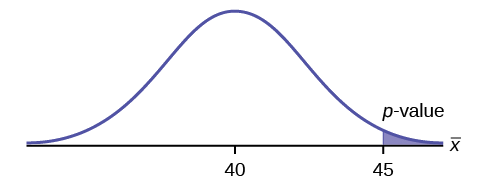
Porque$p < \alpha$, rechazamos la hipótesis nula. Hay pruebas suficientes para sugerir que el cambio en el agarre mejoró la distancia de lanzamiento de Marco.

Nota Histórica

La forma tradicional de comparar las dos probabilidades,$\alpha$ y la$p-\text{value}$, es comparar el valor crítico ($z$-score from$\alpha$) con el estadístico de prueba ($z$-score de datos). El estadístico de prueba calculado para el$p$ valor -es —2.08. (Del Teorema del Límite Central, la fórmula estadística de prueba es$z = \frac{\bar{x}-\mu_{x}}{\left(\frac{\sigma_{x}}{\sqrt{n}}\right)}$. Para este problema,$\bar{x} = 16$,$\mu_{x} = 16.43$ de las hipótesis nulas es,$\sigma_{x} = 0.8$, y$n = 15$.) Puede encontrar el valor crítico para$\alpha = 0.05$ en la tabla normal (ver 15.Tablas en la Tabla de Contenidos). El$z$ puntaje -score para un área a la izquierda igual a 0.05 está a mitad de camino entre —1.65 y —1.64 (0.05 está a mitad de camino entre 0.0505 y 0.0495). El$z$ puntaje -es —1.645. Desde —1.645 > —2.08 (lo que demuestra que$\alpha > p-\text{value}$), rechazar$H_{0}$. Tradicionalmente, la decisión de rechazar o no rechazar se hacía de esta manera. Hoy en día, comparar las dos probabilidades$\alpha$ y el$p$ -valor es muy común. Para este problema, el$p-\text{value}$, 0.0187 es considerablemente menor que$\alpha = 0.05$. Puedes estar seguro de tu decisión de rechazar. El gráfico muestra$\alpha$, el$p-\text{value}$, y las estadísticas de prueba y el valor crítico.

Curva de distribución comparando el α con el valor p. Valores de -2.15 y -1.645 están en el eje x. Las líneas verticales ascendentes se extienden desde ambos valores hasta la curva. El valor p es igual a 0.0158 y apunta al área a la izquierda de -2.15. α es igual a 0.05 y apunta al área entre los valores de -2.15 y -1.645. — Figura$\PageIndex{9}$

Ejemplo$\PageIndex{5}$

Un entrenador de futbol universitario pensó que sus jugadores podían hacer press de banca con un peso medio de 275 libras. Se sabe que la desviación estándar es de 55 libras. Tres de sus jugadores pensaban que el peso medio era más que esa cantidad. Pidieron a 30 de sus compañeros su levantamiento máximo estimado en el ejercicio de press de banca. Los datos oscilaron entre 205 libras y 385 libras. Los diferentes pesos reales fueron (las frecuencias están entre paréntesis) 205 (3); 215 (3); 225 (1); 241 (2); 252 (2); 265 (2); 275 (2); 313 (2); 316 (5); 338 (2); 341 (1); 345 (2); 368 (2); 385 (1).

Realizar una prueba de hipótesis utilizando un nivel de significancia de 2.5% para determinar si la media del press de banca es superior a 275 libras.

Contestar

Configurar la Prueba de Hipótesis:

Dado que el problema es acerca de un peso medio, se trata de una prueba de media de una sola población.

$H_{0}: \mu = 275$
$H_{a}: \mu > 275$

Esta es una prueba de cola derecha.

Cálculo de la distribución necesaria:

Variable aleatoria:$\bar{X} =$ el peso medio, en libras, levantado por los futbolistas.

Distribución para la prueba: Es normal porque$\sigma$ se conoce.

$\bar{X} - N\left(275, \frac{55}{\sqrt{30}}\right)$
$\bar{x} = 286.2$libras (a partir de los datos).
$\sigma = 55$libras (Siempre use$\sigma$ si lo sabe.) Asumimos$\mu = 275$ libras a menos que nuestros datos nos indiquen lo contrario.

Calcular el valor p usando la distribución normal para una media y usando la media de la muestra como entrada (consulte [link] para usar los datos como entrada):

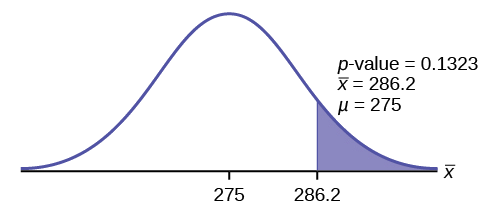
\[p\text{-value} = P(\bar{x} > 286.2) = 0.1323.\nonumber \]

Interpretación del valor p: Si$H_{0}$ es cierto, entonces hay una probabilidad de 0.1331 (13.23%) de que los futbolistas puedan levantar un peso medio de 286.2 libras o más. Debido a que una probabilidad de 13.23% es lo suficientemente grande, un levantamiento de peso medio de 286.2 libras o más no es un evento raro.

Curva de distribución normal del peso promedio levantado por futbolistas con valores de 275 y 286.2 en el eje x. Una línea vertical ascendente se extiende desde 286.2 hasta la curva. El valor p apunta al área a la derecha de 286.2. — Figura$\PageIndex{10}$

Comparar$\alpha$ y el$p-\text{value}$:

$\alpha = 0.025 p-value = 0.1323$

Tomar una decisión: Ya que$\alpha < p\text{-value}$, no rechace$H_{0}$.

Conclusión: Al nivel de significancia de 2.5%, a partir de los datos de la muestra, no hay evidencia suficiente para concluir que el peso real levantado sea superior a 275 libras.

El$p-\text{value}$ se puede calcular fácilmente.

Poner los datos y frecuencias en listas. Presiona STAT y flecha hacia PRUEBAS. Presione 1:Z-Test. Flecha la flecha hacia Datos y presiona ENTRAR. Flecha hacia abajo e ingresa 275 para$\mu_{0}$$\sigma$, 55 para, el nombre de la lista donde pones los datos, y el nombre de la lista donde pones las frecuencias. Flecha hacia abajo a$\mu$: y flecha sobre a$> \mu_{0}$. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. La calculadora no solo calcula el$p-\text{value}$ ($p = 0.1331$), un poco diferente del cálculo anterior - en él usamos la media muestral redondeada a un decimal en lugar de los datos) sino que también calcula el estadístico de prueba (z -score) para la media muestral, la media muestral, y la desviación estándar de la muestra. $\mu > 275$es la hipótesis alternativa. Vuelva a hacer este conjunto de instrucciones excepto la flecha para Dibujar (en lugar de Calcular). Presione ENTER. Aparece una gráfica sombreada con$z = 1.112$ (estadística de prueba) y$p = 0.1331$ ($p-\text{value})$. Asegúrate de que al usar Dibujar no se resalten otras ecuaciones$Y =$ y que las gráficas estén desactivadas.

Ejemplo$\PageIndex{6}$

Los estudiantes de estadística creen que la puntuación media en la primera prueba estadística es 65. Un instructor de estadística piensa que la puntuación media es superior a 65. Muestrea diez estudiantes de estadística y obtiene las puntuaciones 65 65 70 67 66 63 63 68 72 71. Realiza una prueba de hipótesis utilizando un nivel de significancia del 5%. Se supone que los datos provienen de una distribución normal.

Contestar

Configurar la prueba de hipótesis:

Un nivel de significancia del 5% significa eso$\alpha = 0.05$. Se trata de una prueba de media de una sola población.

$H_{0}: \mu = 65 H_{a}: \mu > 65$

Dado que el instructor piensa que el puntaje promedio es mayor, use un "$>$”. El "$>$" significa que la prueba es de cola derecha.

Determinar la distribución necesaria:

Variable aleatoria: puntaje$\bar{X} =$ promedio en la primera prueba estadística.

Distribución para la prueba: Si lees el problema detenidamente, notarás que no hay ninguna desviación estándar poblacional dada. Solo se le dan valores$n = 10$ de datos de muestra. Observe también que los datos provienen de una distribución normal. Esto quiere decir que la distribución para la prueba es de un estudiante$t$.

Uso$t_{df}$. Por lo tanto, la distribución para la prueba es$t_{9}$ dónde$n = 10$ y$df = 10 - 1 = 9$.

Calcula el$p$ valor -usando la$t$ distribución -del estudiante:

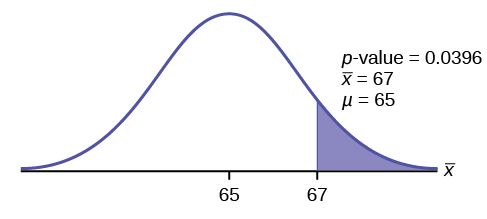
$p\text{-value} = P(\bar{x} > 67) = 0.0396$donde la media de la muestra y la desviación estándar de la muestra se calculan como 67 y 3.1972 a partir de los datos.

Interpretación del valor p: Si la hipótesis nula es verdadera, entonces hay una probabilidad de 0.0396 (3.96%) de que la media muestral sea 65 o más.

Curva de distribución normal de puntuaciones promedio en las primeras pruebas estadísticas con 65 y 67 valores en el eje x. Una línea vertical ascendente se extiende desde 67 hasta la curva. El valor p apunta al área a la derecha de 67. — Figura$\PageIndex{11}$

Comparar$\alpha$ y el$p-\text{value}$:

Desde$α = 0.05$ y$p\text{-value} = 0.0396$. $\alpha > p\text{-value}$.

Tomar una decisión: Desde$\alpha > p\text{-value}$, rechazar$H_{0}$.

Esto significa que rechazas$\mu = 65$. En otras palabras, crees que el puntaje promedio de la prueba es superior a 65.

Conclusión: A un nivel de significancia del 5%, los datos de la muestra muestran evidencia suficiente de que la puntuación media (promedio) de la prueba es mayor a 65, tal como piensa el instructor de matemáticas.

El$p\text{-value}$ se puede calcular fácilmente.

Poner los datos en una lista. Presiona STAT y flecha hacia PRUEBAS. Presione 2:T-Test. Flecha la flecha hacia Datos y presiona ENTRAR. Flecha hacia abajo e ingresa 65 para$\mu_{0}$, el nombre de la lista donde pones los datos, y 1 para Freq:. Flecha hacia abajo a$\mu$: y flecha sobre a$> \mu_{0}$. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. La calculadora no solo calcula la$p\text{-value}$ (p = 0.0396) sino que también calcula el estadístico de prueba (t -score) para la media de la muestra, la media de la muestra y la desviación estándar de la muestra. $\mu > 65$es la hipótesis alternativa. Vuelva a hacer este conjunto de instrucciones excepto la flecha para Dibujar (en lugar de Calcular). Presione ENTER. Aparece una gráfica sombreada con$t = 1.9781$ (estadística de prueba) y$p = 0.0396$ ($p\text{-value}$). Asegúrate de que al usar Dibujar no se resalten otras ecuaciones$Y =$ y que las gráficas estén desactivadas.

Ejercicio$\PageIndex{6}$

Se cree que un precio de acciones para una compañía en particular crecerá a una tasa de 5 dólares semanales con una desviación estándar de $1. Un inversionista cree que las acciones no crecerán tan rápido. Los cambios en el precio de las acciones se registran por diez semanas y son los siguientes: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Realizar una prueba de hipótesis utilizando un nivel de significancia del 5%. Indique las hipótesis nulas y alternativas, encuentre el valor p, indique su conclusión e identifique los errores Tipo I y Tipo II.

Contestar

$H_{0}: \mu = 5$
$H_{a}: \mu < 5$
$p = 0.0082$

Porque$p < \alpha$, rechazamos la hipótesis nula. Hay pruebas suficientes para sugerir que el precio de las acciones de la compañía crece a una tasa inferior a 5 dólares semanales.

Tipo I Error: Para concluir que el precio de las acciones está creciendo más lento que 5 dólares a la semana cuando, de hecho, el precio de las acciones está creciendo a 5 dólares semanales (rechazar la hipótesis nula cuando la hipótesis nula es cierta).
Error Tipo II: Para concluir que el precio de las acciones está creciendo a una tasa de 5 dólares semanales cuando, de hecho, el precio de las acciones está creciendo más lentamente que 5 dólares semanales (no rechace la hipótesis nula cuando la hipótesis nula es falsa).

Ejemplo$\PageIndex{7}$

Joon cree que el 50% de las novias primerizas en Estados Unidos son más jóvenes que sus novios. Realiza una prueba de hipótesis para determinar si el porcentaje es igual o diferente del 50%. Joon muestra a 100 novias primerizas y 53 responden que son más jóvenes que sus novios. Para la prueba de hipótesis, utiliza un nivel de significancia del 1%.

Contestar

Configurar la prueba de hipótesis:

El nivel de significancia de 1% significa que α = 0.01. Esta es una prueba de una sola proporción poblacional.

$H_{0}: p = 0.50$$H_{a}: p \neq 0.50$

Las palabras “es igual o diferente de” te dicen que esta es una prueba de dos colas.

Calcular la distribución necesaria:

Variable aleatoria:$P′ =$ el porcentaje de novias primerizas que son más jóvenes que sus novios.

Distribución para la prueba: El problema no contiene mención de una media. La información se da en términos de porcentajes. Utilizar la distribución para P′, la proporción estimada.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

Por lo tanto,

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

dónde$p = 0.50, q = 1−p = 0.50$, y$n = 100$

Calcular el valor p usando la distribución normal para proporciones:

\[p\text{-value} = P(p′ < 0.47 \space or \space p′ > 0.53) = 0.5485\nonumber \]

donde\[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretación del valor p: Si la hipótesis nula es verdadera, hay 0.5485 probabilidad (54.85%) de que la proporción muestral (estimada)$p'$ sea 0.53 o más OR 0.47 o menos (ver la gráfica en la Figura).

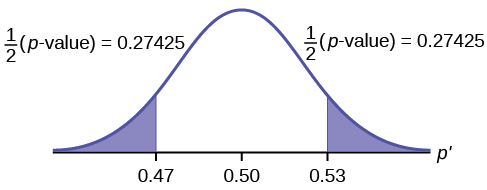
Curva de distribución normal del porcentaje de novias primerizas que son más jóvenes que el novio con valores de 0.47, 0.50 y 0.53 en el eje x. Las líneas verticales ascendentes se extienden desde 0.47 y 0.53 hasta la curva. Se calcula 1/2 (valores p) para las áreas exteriores de 0.47 y 0.53. — Figura$\PageIndex{12}$

$\mu = p = 0.50$proviene de$H_{0}$, la hipótesis nula.

$p′ = 0.53$. Dado que la curva es simétrica y la prueba es de dos colas, la$p′$ para la cola izquierda es igual a$0.50 – 0.03 = 0.47$ donde$\mu = p = 0.50$. (0.03 es la diferencia entre 0.53 y 0.50.)

Comparar$\alpha$ y el$p\text{-value}$:

Desde$\alpha = 0.01$ y$p\text{-value} = 0.5485$. $\alpha < p\text{-value}$.

Tomar una decisión: Ya que$\alpha < p\text{-value}$, no se puede rechazar$H_{0}$.

Conclusión: Al nivel de significancia del 1%, los datos de la muestra no muestran evidencia suficiente de que el porcentaje de novias primerizas que son más jóvenes que sus novios sea diferente del 50%.

El$p\text{-value}$ se puede calcular fácilmente.

Presiona STAT y flecha hacia PRUEBAS. Prensa 5:1 -PropzTest. Ingresa .5 para$p_{0}$, 53 para$x$ y 100 para$n$. Flecha hacia abajo a Prop y flecha a no es igual$p_{0}$. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. La calculadora calcula el$p\text{-value}$ ($p = 0.5485$) y el estadístico de prueba ($z$-score). Prop no es igual a .5 es la hipótesis alternativa. Vuelva a hacer este conjunto de instrucciones excepto la flecha para Dibujar (en lugar de Calcular). Presione ENTER. Aparece una gráfica sombreada con$z = 0.6$ (estadística de prueba) y$p = 0.5485$ ($p\text{-value}$). Asegúrate de que al usar Dibujar no se resalten otras ecuaciones$Y =$ y que las gráficas estén desactivadas.

Los errores Tipo I y Tipo II son los siguientes:

El error Tipo I es concluir que la proporción de novias primerizas que son más jóvenes que sus novios es diferente del 50% cuando, de hecho, la proporción es en realidad del 50%. (Rechazar la hipótesis nula cuando la hipótesis nula es verdadera).

El error Tipo II es que no hay evidencia suficiente para concluir que la proporción de novias primerizas que son más jóvenes que sus novios difiere del 50% cuando, de hecho, la proporción sí difiere del 50%. (No rechace la hipótesis nula cuando la hipótesis nula sea falsa).

Ejercicio$\PageIndex{7}$

Un maestro cree que el 85% de los estudiantes de la clase querrán ir de excursión al zoológico local. Realiza una prueba de hipótesis para determinar si el porcentaje es igual o diferente del 85%. El maestro toma muestras a 50 alumnos y 39 responden que querrían ir al zoológico. Para la prueba de hipótesis, use un nivel de significancia de 1%.

Primero, determina qué tipo de prueba es esta, configura la prueba de hipótesis, encuentra la$p\text{-value}$, dibuja la gráfica y expone tu conclusión.

Contestar

Dado que el problema es sobre porcentajes, esta es una prueba de proporciones de una sola población.

$H_{0} : p = 0.85$
$H_{a}: p \neq 0.85$
$p = 0.7554$

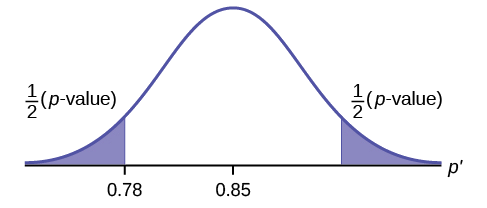
Porque$p > \alpha$, fallamos en rechazar la hipótesis nula. No hay evidencia suficiente para sugerir que la proporción de estudiantes que quieren ir al zoológico no es del 85%.

Ejemplo$\PageIndex{8}$

Supongamos que un grupo de consumidores sospecha que la proporción de hogares que tienen tres teléfonos celulares es del 30%. Una compañía de telefonía celular tiene razones para creer que la proporción no es del 30%. Antes de iniciar una gran campaña publicitaria, realizan una prueba de hipótesis. Su gente de marketing encuestó a 150 hogares con el resultado de que 43 de los hogares cuentan con tres teléfonos celulares.

Contestar

Configurar la Prueba de Hipótesis:

$H_{0}: p = 0.30, H_{a}: p \neq 0.30$

Determinar la distribución necesaria:

La variable aleatoria es la$P′ =$ proporción de hogares que cuentan con tres teléfonos celulares.

La distribución para la prueba de hipótesis es$P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)$

Ejercicio$\PageIndex{8}$.2

a. El valor que ayuda a determinar el$p\text{-value}$ es$p′$. Calcular$p′$.

Contestar

a.$p' = \frac{x}{n}$ donde$x$ es el número de éxitos y$n$ es el número total en la muestra.

$x = 43, n = 150$

$p′ = 43150$

Ejercicio$\PageIndex{8}$.3

b. ¿Qué es un éxito para este problema?

Contestar

b. Un éxito es contar con tres teléfonos celulares en un hogar.

Ejercicio$\PageIndex{8}$.4

c. ¿Cuál es el nivel de significación?

Contestar

c. El nivel de significancia es el preestablecido$\alpha$. Ya que no$\alpha$ se da, asuma eso$\alpha = 0.05$.

Ejercicio$\PageIndex{8}$.5

d. Dibuja la gráfica para este problema. Dibuja el eje horizontal. Etiquete y sombree apropiadamente.

Calcular el$p\text{-value}$.

Contestar

d.$p\text{-value} = 0.7216$

Ejercicio$\PageIndex{8}$.6

e. Tomar una decisión. _____________ (Rechazar/No rechazar)$H_{0}$ porque____________.

Contestar

e. suponiendo que$\alpha = 0.05, \alpha < p\text{-value}$. La decisión es no rechazar$H_{0}$ porque no hay pruebas suficientes para concluir que la proporción de hogares que tienen tres celulares no es del 30%.

Ejercicio$\PageIndex{8}$

Los especialistas en marketing creen que 92% de los adultos en Estados Unidos poseen un teléfono celular. Un fabricante de celulares cree que ese número es en realidad menor. Se encuestan a 200 adultos estadounidenses, de los cuales, 174 reportan tener celulares. Utilizar un nivel de significancia del 5%. Indique la hipótesis nula y alternativa, encuentre el valor p, indique su conclusión e identifique los errores Tipo I y Tipo II.

Contestar

$H_{0}: p = 0.92$
$H_{a}: p < 0.92$
$p\text{-value} = 0.0046$

Porque$p < 0.05$, rechazamos la hipótesis nula. Existe evidencia suficiente para concluir que menos del 92% de los adultos estadounidenses poseen teléfonos celulares.

Error tipo I: Para concluir que menos del 92% de los adultos estadounidenses poseen celulares cuando, de hecho, 92% de los adultos estadounidenses sí poseen celulares (rechazar la hipótesis nula cuando la hipótesis nula es cierta).
Error tipo II: Concluir que 92% de los adultos estadounidenses poseen celulares cuando, de hecho, menos del 92% de los adultos estadounidenses poseen celulares (no rechacen la hipótesis nula cuando la hipótesis nula es falsa).

El siguiente ejemplo es un poema escrito por una estudiante de estadística llamada Nicole Hart. La solución al problema sigue al poema. Observe que la prueba de hipótesis es para una sola proporción de población. Esto significa que las hipótesis nulas y alternativas utilizan el parámetro$p$. La distribución para la prueba es normal. La proporción estimada$p′$ es la proporción de pulgas muertas con respecto al total de pulgas encontradas en Fido. Esta es información de muestra. El problema da un cálculo preconcebido$\alpha = 0.01$, para comparación, y un intervalo de confianza del 95%. El poema es ingenioso y humorístico, ¡así que por favor disfrútalo!

Ejemplo$\PageIndex{9}$

Mi perro tiene tantas pulgas,

No se desprenden con facilidad.
En cuanto al shampoo, he probado muchos tipos
Incluso uno llamado Bubble Hype,
Que solo mató al 25% de las pulgas,
Desafortunadamente no me complació.

He usado todo tipo de jabón,
Hasta que había perdido la esperanza
Hasta que un día vi
Un anuncio que me puso en asombro.

Un champú usado para perros
LLAMADO LO SUFICIENTE BUENO para limpiar un cerdo
Garantizado para matar más pulgas.

Le di un baño a Fido
Y después de hacer los cálculos
Su número de pulgas ¡
Empezó a caer a las 3's!
Antes de su champú
conté 42.

Al final de su baño,
rehice las matemáticas
Y el nuevo champú había matado a 17 pulgas.
Entonces ahora me quedé complacido.

Ahora es el momento de que te diviertas un poco
Con el nivel de significación siendo .01,
debes ayudarme a averiguar

¿Usa el nuevo shampoo o te quedas sin?

Contestar

Configurar la prueba de hipótesis:

$H_{0}: p \leq 0.25$$H_{a}: p > 0.25$

Determinar la distribución necesaria:

En palabras, indique CLARAMENTE cuál es su variable aleatoria$\bar{X}$ o$P′$ representa.

$P′ =$La proporción de pulgas que son asesinadas por el nuevo champú

Indicar la distribución a utilizar para la prueba.

Normal:

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

Estadística de prueba:$z = 2.3163$

Calcular el$p\text{-value}$ usando la distribución normal para proporciones:

\[p\text{-value} = 0.0103\nonumber \]

En una o dos oraciones completas, explique qué significa el valor p para este problema.

Si la hipótesis nula es verdadera (la proporción es 0.25), entonces hay una probabilidad de 0.0103 de que la proporción muestral (estimada) sea 0.4048$\left(\frac{17}{42}\right)$ o más.

Utilice la información anterior para esbozar una imagen de esta situación. CLARAMENTE, etiquetar y escalar el eje horizontal y sombrear la (s) región (es) correspondiente (s) al$p\text{-value}$.

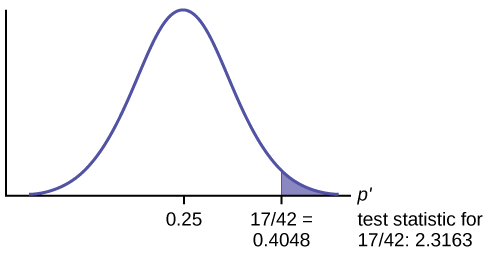
Gráfico de distribución normal de la proporción de pulgas muertas por el nuevo champú con valores de 0.25 y 0.4048 en el eje x. Una línea vertical hacia arriba se extiende desde 0.4048 hasta la curva y el área a la izquierda de ésta está sombreada. Se enumera el estadístico de prueba de la proporción muestral. — Figura$\PageIndex{14}$

Comparar$\alpha$ y el$p\text{-value}$:

Indicar la decisión correcta (“rechazar” o “no rechazar” la hipótesis nula), el motivo de la misma, y escribir una conclusión apropiada, utilizando oraciones completas.

alfa	decisión	motivo de decisión
0.01	No rechazar$H_{0}$	$\alpha < p\text{-value}$

Conclusión: Al nivel de significancia del 1%, los datos de la muestra no muestran evidencia suficiente de que el porcentaje de pulgas que son asesinadas por el nuevo champú sea superior al 25%.

Construir un intervalo de confianza del 95% para la media o proporción verdadera. Incluir un boceto de la gráfica de la situación. Etiquetar la estimación del punto y los límites inferior y superior del intervalo de confianza.

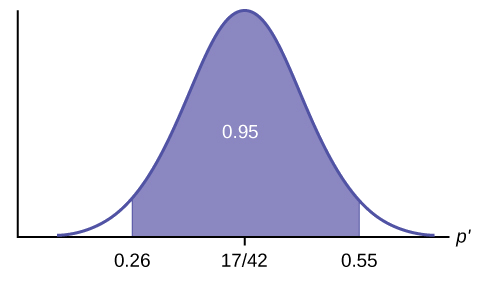
Gráfico de distribución normal de la proporción de pulgas muertas por el nuevo champú con valores de 0.26, 17/42 y 0.55 en el eje x. Una línea vertical ascendente se extiende desde 0.26 y 0.55. El área entre estos dos puntos es igual a 0.95. — Figura$\PageIndex{15}$

Intervalo de confianza: (0.26,0.55) Estamos 95% seguros de que la verdadera proporción poblacional p de pulgas que son asesinadas por el nuevo champú está entre 26% y 55%.

Este resultado de prueba no es muy definitivo ya que el$p\text{-value}$ está muy cerca del alfa. En realidad, uno probablemente haría más pruebas al darle otro baño al perro después de que las pulgas hayan tenido la oportunidad de regresar.

Ejemplo$\PageIndex{10}$

El Instituto Nacional de Estándares y Tecnología proporciona datos exactos sobre las propiedades de conductividad de los materiales. Las siguientes son las mediciones de conductividad para 11 piezas seleccionadas al azar de un tipo particular de vidrio.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

¿Hay pruebas convincentes de que la conductividad promedio de este tipo de vidrio es mayor a uno? Utilizar un nivel de significancia de 0.05. Supongamos que la población es normal.

Contestar

Sigamos un proceso de cuatro pasos para responder a esta pregunta estadística.

Indicar la Pregunta: Necesitamos determinar si, a un nivel de significancia 0.05, la conductividad promedio del vidrio seleccionado es mayor a uno. Nuestras hipótesis serán
1. $H_{0}: \mu \leq 1$
2. $H_{a}: \mu > 1$
Plan: Estamos probando una media muestral sin una desviación estándar poblacional conocida. Por lo tanto, necesitamos usar una distribución Student's-T. Supongamos que la población subyacente es normal.
Hacer los cálculos: Ingresaremos los datos de la muestra en el TI-83 de la siguiente manera.

4. Indicar las Conclusiones: Dado que el$p\text{-value} (p = 0.036)$ es menor que nuestro valor alfa, rechazaremos la hipótesis nula. Es razonable afirmar que los datos respaldan la afirmación de que el nivel de conductividad promedio es mayor a uno.

Ejemplo$\PageIndex{11}$

En un estudio de 420.019 usuarios de teléfonos celulares, 172 de los sujetos desarrollaron cáncer cerebral. Pruebe la afirmación de que los usuarios de teléfonos celulares desarrollaron cáncer cerebral a un ritmo mayor que el de los usuarios que no son celulares (la tasa de cáncer cerebral para los usuarios que no son de teléfonos celulares es de 0.0340%). Dado que este es un tema crítico, use un nivel de significancia 0.005. Explique por qué el nivel de significancia debe ser tan bajo en términos de un error de Tipo I.

Contestar

Seguiremos el proceso de cuatro pasos.

Necesitamos realizar una prueba de hipótesis sobre la tasa de cáncer reclamada. Nuestras hipótesis serán
1. $H_{0}: p \leq 0.00034$
2. $H_{a}: p > 0.00034$
Si cometemos un error de Tipo I, esencialmente estamos aceptando una afirmación falsa. Dado que la afirmación describe entornos causantes de cáncer, queremos minimizar las posibilidades de identificar incorrectamente las causas del cáncer.
Estaremos probando una proporción de muestra con$x = 172$ y$n = 420,019$. La muestra es suficientemente grande porque tenemos$np = 420,019(0.00034) = 142.8$$nq = 420,019(0.99966) = 419,876.2$, dos resultados independientes y una probabilidad fija de éxito$p = 0.00034$. Así podremos generalizar nuestros resultados a la población.
Los resultados de TI asociados son

Figura$\PageIndex{11}$.

Figura$\PageIndex{12}$.
Dado que el$p\text{-value} = 0.0073$ es mayor que nuestro valor alfa$= 0.005$, no podemos rechazar el nulo. Por lo tanto, concluimos que no hay evidencia suficiente para respaldar la afirmación de mayores tasas de cáncer cerebral para los usuarios de teléfonos celulares.

Ejemplo$\PageIndex{12}$

Según el Censo de Estados Unidos hay aproximadamente 268,608,618 residentes de 12 años o más. Las estadísticas de la Red Nacional de Violación, Abuso e Incesto indican que, en promedio, cada año ocurren 207 mil 754 violaciones (masculinas y femeninas) para personas de 12 años y mayores. Esto se traduce en un porcentaje de agresiones sexuales de 0.078%. En el condado de Daviess, KY, se reportaron 11 violaciones para una población de 37 mil 937. Realizar una prueba de hipótesis apropiada para determinar si existe una diferencia estadísticamente significativa entre el porcentaje local de agresión sexual y el porcentaje nacional de agresión sexual. Utilizar un nivel de significancia de 0.01.

Contestar

Seguiremos el plan de cuatro pasos.

Necesitamos probar si la proporción de agresiones sexuales en el condado de Daviess, KY, es significativamente diferente del promedio nacional.
Ya que se nos presentan proporciones, utilizaremos una prueba z de una proporción. Las hipótesis para la prueba serán
1. $H_{0}: p = 0.00078$
2. $H_{a}: p \neq 0.00078$
Las siguientes capturas de pantalla muestran las estadísticas resumidas de la prueba de hipótesis.

Figura$\PageIndex{13}$.

Figura$\PageIndex{14}$.
Dado que el$p\text{-value}$$p = 0.00063$,, es menor que el nivel alfa de 0.01, los datos de la muestra indican que debemos rechazar la hipótesis nula. En conclusión, los datos de la muestra apoyan la afirmación de que la proporción de agresiones sexuales en el condado de Daviess, Kentucky, es diferente de la proporción promedio nacional.

Revisar

La prueba de hipótesis en sí tiene un proceso establecido. Esto se puede resumir de la siguiente manera:

Determinar$H_{0}$ y$H_{a}$. Recuerden, son contradictorios.
Determinar la variable aleatoria.
Determinar la distribución para la prueba.
Dibuje una gráfica, calcule el estadístico de prueba y use el estadístico de prueba para calcular el$p\text{-value}$. (Un puntaje z y un puntaje t son ejemplos de estadísticas de pruebas).
Comparar el α preconcebido con el valor p, tomar una decisión (rechazar o no rechazar H ₀) y escribir una conclusión clara usando frases en inglés.

Observe que al realizar la prueba de hipótesis, usa$\alpha$ y no$\beta$. $\beta$es necesario para ayudar a determinar el tamaño de la muestra de los datos que se utilizan en el cálculo del$p\text{-value}$. Recuerda que la cantidad$1 – \beta$ se llama el Poder de la Prueba. Una alta potencia es deseable. Si la potencia es demasiado baja, los estadísticos suelen aumentar el tamaño de la muestra manteniendo α igual. Si la potencia es baja, la hipótesis nula podría no ser rechazada cuando debería ser.

Ejercicio$\PageIndex{8}$

Asumir$H_{0}: \mu = 9$ y$H_{a}: \mu < 9$. ¿Es esta una prueba de cola izquierda, de cola derecha o de dos colas?

Contestar

Esta es una prueba de cola izquierda.

Ejercicio$\PageIndex{9}$

Asumir$H_{0}: \mu \leq 6$ y$H_{a}: \mu > 6$. ¿Es esta una prueba de cola izquierda, de cola derecha o de dos colas?

Ejercicio$\PageIndex{10}$

Asumir$H_{0}: p = 0.25$ y$H_{a}: p \neq 0.25$. ¿Es esta una prueba de cola izquierda, de cola derecha o de dos colas?

Contestar

Esta es una prueba de dos colas.

Ejercicio$\PageIndex{11}$

Dibuja la gráfica general de una prueba de cola izquierda.

Ejercicio$\PageIndex{12}$

Dibuja la gráfica de una prueba de dos colas.

Contestar

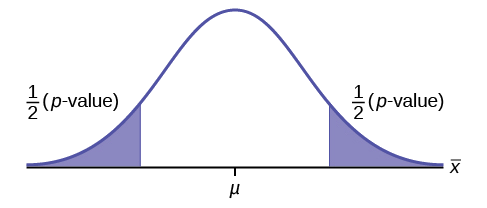
Ejercicio$\PageIndex{13}$

Una botella de agua está etiquetada como que contiene 16 onzas líquidas de agua. Usted cree que es menos que eso. ¿Qué tipo de prueba usarías?

Ejercicio$\PageIndex{14}$

Tu amigo afirma que su media puntuación de golf es de 63. Quieres demostrar que es más alto que eso. ¿Qué tipo de prueba usarías?

Contestar

una prueba de cola derecha

Ejercicio$\PageIndex{15}$

Una báscula de baño afirma poder identificar correctamente cualquier peso dentro de una libra. Piensas que no puede ser tan exacto. ¿Qué tipo de prueba usarías?

Ejercicio$\PageIndex{16}$

Tiras una moneda y registras si muestra la cabeza o la cola. Sabes que la probabilidad de conseguir cabezas es del 50%, pero piensas que es menor para esta moneda en particular. ¿Qué tipo de prueba usarías?

Contestar

una prueba de cola izquierda

Ejercicio$\PageIndex{17}$

Si la hipótesis alternativa tiene un símbolo not equals ($\neq$), ¿sabes usar qué tipo de prueba?

Ejercicio$\PageIndex{18}$

Supongamos que la hipótesis nula establece que la media es de al menos 18. ¿Es esta una prueba de cola izquierda, de cola derecha o de dos colas?

Contestar

Esta es una prueba de cola izquierda.

Ejercicio$\PageIndex{19}$

Supongamos que la hipótesis nula establece que la media es como máximo 12. ¿Es esta una prueba de cola izquierda, de cola derecha o de dos colas?

Ejercicio$\PageIndex{20}$

Supongamos que la hipótesis nula establece que la media es igual a 88. La hipótesis alternativa establece que la media no es igual a 88. ¿Es esta una prueba de cola izquierda, de cola derecha o de dos colas?

Contestar

Esta es una prueba de dos colas.

Referencias

Datos de Amit Schitai. Director de Tecnología Instruccional y Aprendizaje a Distancia. LBCC.
Datos de Bloomberg Businessweek. Disponible en línea en www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
Datos de energy.gov. Disponible en línea en http://energy.gov (consultado el 27 de junio de 2013).
Datos de Gallup®. Disponible en línea en www.gallup.com (consultado el 27 de junio de 2013).
Datos de Creciendo por Grados por Allen y Seaman.
Datos de La Leche League Internacional. Disponible en línea en www.lalecheleague.org/law/bafeb01.html.
Datos de la American Automobile Association. Disponible en línea en www.aaa.com (consultado el 27 de junio de 2013).
Datos de la American Library Association. Disponible en línea en www.ala.org (consultado el 27 de junio de 2013).
Datos de la Oficina de Estadísticas del Trabajo. Disponible en línea en http://www.bls.gov/oes/current/oes291111.htm.
Datos de los Centros para el Control y la Prevención de Enfermedades. Disponible en línea en www.cdc.gov (consultado el 27 de junio de 2013)
Datos de la Oficina del Censo de Estados Unidos, disponibles en línea en quickfacts.census.gov/qfd/estados/00000.html (consultado el 27 de junio de 2013).
Datos de la Oficina del Censo de Estados Unidos. Disponible en línea en www.census.gov/hhes/socdemo/language/.
Datos de Toastmasters International. Disponible en línea en http://toastmasters.org/artisan/deta...eID=429&Page=1.
Datos de Weather Underground. Disponible en línea en www.wunderground.com (consultado el 27 de junio de 2013).
Buró Federal de Investigaciones. “Informes uniformes de delitos e índice de delitos en Daviess en el estado de Kentucky aplicados por el condado de Daviess de 1985 a 2005”. Disponible en línea en http://www.disastercenter.com/kentucky/crime/3868.htm (consultado el 27 de junio de 2013).
“Foothill-De Anza Community College District”. Colegio De Anza, Invierno 2006. Disponible en línea en Research.fhda.edu/factbook/da... t_da_2006w.pdf.
Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Los teléfonos celulares y el cáncer: un estudio de cohorte a nivel nacional en Dinamarca”. Instituto de Epidemiología del Cáncer y la Sociedad Danesa del Cáncer, 93 (3) :203-7. Disponible en línea en http://www.ncbi.nlm.nih.gov/pubmed/11158188 (consultado el 27 de junio de 2013).
Red Nacional de Violación, Abuso e Incesto. “¿Con qué frecuencia ocurre la agresión sexual?” RAINN, 2009. Disponible en línea en www.rainn.org/get-information... sexual-assault (consultado el 27 de junio de 2013).

Glosario

Teorema de Límite Central: Dada una variable aleatoria (RV) con media conocida$\mu$ y desviación estándar conocida$\sigma$. Estamos muestreando con tamaño$n$ y estamos interesados en dos nuevas RVs: la media de la muestra$\bar{X}$, y la suma de la muestra,$\sum X$. Si el tamaño$n$ de la muestra es suficientemente grande, entonces$\bar{X} - N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)$ y$\sum X - N \left(n\mu, \sqrt{n}\sigma\right)$. Si el tamaño n de la muestra es suficientemente grande, entonces la distribución de las medias de la muestra y la distribución de las sumas de la muestra se aproximarán a una distribución normal independientemente de la forma de la población. La media de las medias de la muestra será igual a la media de la población y la media de las sumas de la muestra será igual a$n$ veces la media de la población. La desviación estándar de la distribución de las medias muestrales$\frac{\sigma}{\sqrt{n}}$,, se denomina error estándar de la media.

Search

Text Color

Text Size

Margin Size

Font Type