5: Prueba de hipótesis
( \newcommand{\kernel}{\mathrm{null}\,}\)
Desde el inicio del texto se ha enfatizado que una razón primordial para hacer estadísticas es tomar una decisión. Se pueden tomar mejores decisiones si se basan en la mejor evidencia disponible. Si bien la situación ideal sería obtener datos de toda la población, la realidad es que los datos casi siempre vendrán de una muestra. Debido a que los datos de la muestra varían en función del proceso aleatorio que se utilizó para seleccionarlo, el investigador se ve obligado a usar datos de muestra para sacar una conclusión sobre toda la población. Esto es inferencia. Se está utilizando evidencia parcial específica para llegar a una conclusión más general.
En el Capítulo 5, se desarrollaron fórmulas para probar hipótesis sobre proporciones y medias. En el primer caso la fórmula era
z=ˆp−pp(1−p)n
y en este último caso fue
z=ˉx−μσ√n.
En general, estas fórmulas generan un estadístico de prueba, z, que se utiliza para determinar el número de errores estándar que un estadístico es a partir de un parámetro. Luego se utiliza la distribución normal para determinar la probabilidad de obtener esa estadística, o una estadística más extrema. Esa probabilidad se llama valor p.
Cada número que se necesita para hacer uso de la fórmula
z=ˆp−pp(1−p)n
se pueden encontrar en la hipótesis nula (p) o a partir de los datos (ˆp,n). No se puede decir lo mismo de la fórmula
z=ˉx−μσ√n.
Si bien el valor paraμ proviene de la hipótesis nula y el valor deˉx y n provienen de los datos de muestra, no hay forma de obtener el valor deσ sin hacer un censo. En el último capítulo siempre te dijeron el valor deσ, pero esto no sucede en el mundo real porque para encontrarσ requiere primero encontrarμ y si supierasμ, no habría razón para probar una hipótesis al respecto.
La resolución de este problema requiere de dos cambios en el proceso que se utilizó en el capítulo anterior. El primer cambio es que tendremos que estimarσ. La mejor estimación es s, la desviación estándar de la muestra. Reemplazarσ con s significa que ya no podemos usar la distribución normal estándar (distribución z). Por lo tanto, el segundo cambio es encontrar una distribución más adecuada que pueda utilizarse para modelar la distribución de las medias muestrales.
Se utiliza un conjunto de distribuciones llamadas distribuciones t cuando el error estándar de la media,σˉx=σ√n se sustituye por el error estándar estimado de la mediasˉx=s√n. La fórmula z para las medias,
z=ˉx−μσ√n
luego se modifica para convertirse en la fórmula t
t=ˉx−μs√n.
Observe que la única diferencia es el uso de s en lugar deσ. Se utilizan las distribuciones t porque proporcionan una mejor aproximación de la distribución de medias muestrales cuando la desviación estándar de la población debe estimarse utilizando la desviación estándar de la muestra.
A diferencia de la distribución normal, hay muchas distribuciones t, siendo cada una definida por el número de grados de libertad. Grados de Libertad son un nuevo concepto que requiere un poco de explicación.
El concepto de grados de libertad tiene que ver con el número de valores independientes que pueden identificar una posición. Esto puede ser más fácil de pensar si imaginas un sistema de coordenadas cartesianas. Con dos valores elegidos independientemente, normalmente llamados x e y, la posición de un punto se puede ubicar en algún lugar de la gráfica. En consecuencia, el punto que se escoge tiene dos grados de libertad. Sin embargo, si se coloca una restricción en los puntos, como x + y = 3, entonces solo uno de los valores puede ser independiente y el otro valor dependerá del valor independiente. Debido a la restricción, se ha perdido un grado de libertad por lo que ahora el punto solo tiene un grado de libertad. Si se coloca una segunda restricción en el sistema, como x — y = 1, entonces se pierde otro grado de libertad. Los grados de libertad se pierden cada vez que se aplica una restricción.
Para los datos de la muestra, cada valor representa una nueva evidencia, siempre que los datos sean independientes. Los datos dependientes inflarían artificialmente el tamaño de la muestra sin proporcionar más información. Dado que un tamaño de muestra mayor produciría un error estándar menor, lo que llevaría a un valor t mayor y por lo tanto aumentaría la probabilidad de una conclusión estadísticamente significativa, entonces es importante contar solo el número de valores de datos independientes, los cuales se conocen como grados de libertad. Se pierde un grado de libertad cada vez que se reemplaza un parámetro por una estadística. Por lo tanto, cuando el error estándarσbarx=σ√n se convierte en el error estándar estimadosˉx=s√n, se ha perdido un grado de libertad. En este caso, df = n — 1 donde df es una abreviatura de grados de libertad.
La fórmula para generar el estadístico de prueba, t, que se utiliza para determinar el número de errores estándar que una media muestral es a partir de una media hipotética es
t=ˉx−μs√n
Tiene n-1 grados de libertad.
De la misma manera que z = 1 representa 1 desviación estándar por encima de la media para una distribución normal,t=1 representa 1 desviación estándar por encima de la media en una distribución t. Una vezt determinado el valor de, el valor p se puede encontrar buscando en una tabla t.
Distribuciones t Student
| Probabilidad de una cola | 0.4 | 0.25 | 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0005 |
| Probabilidad de dos colas | 0.8 | 0.5 | 0.2 | 0.1 | 0.05 | 0.02 | 0.01 | 0.001 |
| Nivel de Confianza | 20% | 50% | 80% | 90% | 95% | 98% | 99% | 99.9% |
| df | ||||||||
| 1 | 0.325 | 1.000 | 3.078 | 6.314 | 12.706 | 31.821 | 63.656 | 636.578 |
| 2 | 0.289 | 0.816 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 31.600 |
| 3 | 0.277 | 0.765 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 12.924 |
| 4 | 0.271 | 0.741 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 8.610 |
| 5 | 0.267 | 0.727 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 6.869 |
| 6 | 0.265 | 0.718 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 5.959 |
| 7 | 0.263 | 0.711 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 5.408 |
| 8 | 0.262 | 0.706 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 5.041 |
| 9 | 0.261 | 0.703 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 4.781 |
| 10 | 0.260 | 0.700 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.587 |
| 11 | 0.260 | 0.697 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 4.437 |
| 12 | 0.259 | 0.695 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 4.318 |
| 13 | 0.259 | 0.694 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 4.221 |
| 14 | 0.258 | 0.692 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 4.140 |
| 15 | 0.258 | 0.691 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 4.073 |
| 16 | 0.258 | 0.690 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 4.015 |
| 17 | 0.257 | 0.689 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.965 |
| 18 | 0.257 | 0.689 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.922 |
| 19 | 0.257 | 0.688 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.883 |
| 20 | 0.257 | 0.687 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.850 |
| 21 | 0.257 | 0.686 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.819 |
| 22 | 0.256 | 0.686 | 1.321 | 1.717 | 2.074 | 2.608 | 2.819 | 3.792 |
| 23 | 0.256 | 0.685 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.768 |
| 24 | 0.256 | 0.685 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.745 |
| 25 | 0.256 | 0.684 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.745 |
| 26 | 0.256 | 0.684 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.707 |
| 27 | 0.256 | 0.684 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.689 |
| 28 | 0.256 | 0.683 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.674 |
| 29 | 0.256 | 0.683 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.660 |
| 30 | 0.256 | 0.683 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.646 |
| 40 | 0.255 | 0.681 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 3.551 |
| 60 | 0.254 | 0.679 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.460 |
| 120 | 0.254 | 0.677 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 3.373 |
| z∗ | 0.253 | 0.674 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 3.290 |
Una suposición cuando se utilizan distribuciones t con un tamaño de muestra pequeño es que la muestra se extrae de una población normalmente distribuida. Si bien algunos investigadores creen que esta estadística de prueba es lo suficientemente robusta como para tolerar alguna violación de esta suposición, como mínimo, se debe ver un histograma de los datos para ver si la suposición parece realista. De no ser así, deberán perseguirse otros métodos de análisis no discutidos en este texto.
La forma en que se usa esta tabla t para determinar un valor p es encontrar primero la fila con el número apropiado de grados de libertad. En esa fila, localice el rango que contendría el estadístico de prueba. Sube a la primera fila si estás haciendo una prueba de una cola o la segunda fila si es una prueba de dos colas. A continuación, identificar la ubicación del alfa. Si tu valor p es mayor que alfa entonces usa un símbolo de desigualdad para mostrarlo. Si tu valor p es menor que alfa, entonces muéstralo con un símbolo de desigualdad. Si se puede proporcionar mayor detalle, debería serlo. Dado que las distribuciones t son simétricas, los valores t negativos se pueden encontrar en esta tabla ignorando los signos negativos y asumiendo que las áreas de la primera fila están a la izquierda. A continuación se presentan 2 ejemplos. En cada ejemplo se proporciona el signo en la hipótesis alternativa, el nivel de significancia, los grados de libertad y el valor t.
1. H1:>α=0.05df = 6, t = 2.3
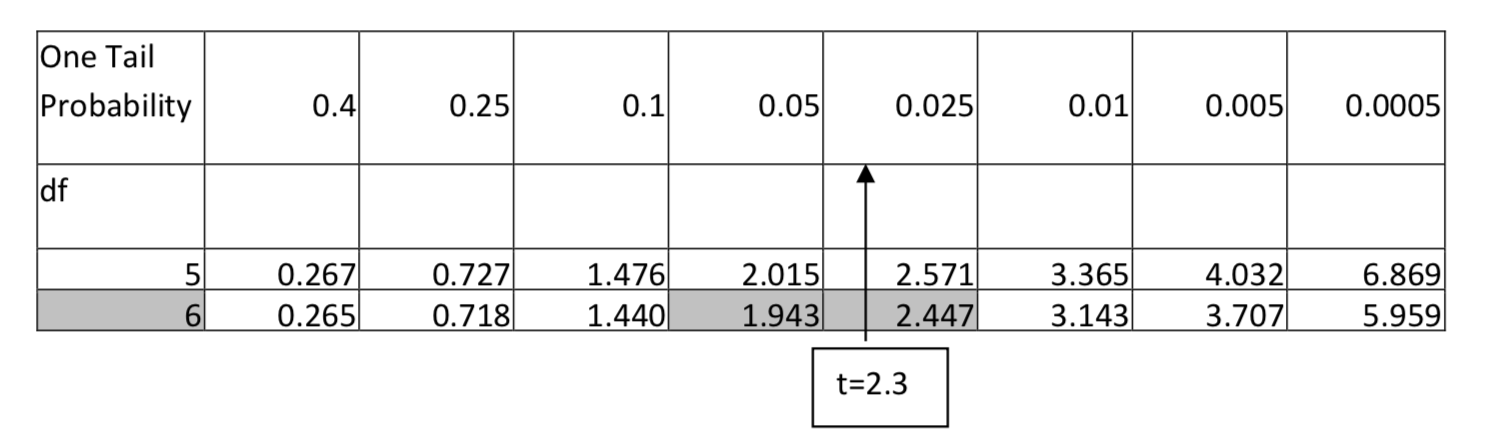
Para 6 grados de libertad, 2.3 cae entre 1.943 y 2.447, lo que significa que tiene un área en la cola que está entre 0.05 y 0.025. El valor p se reportaría como p < 0.05.
2. H1:≠α=0.01df = 18, t = -1.26
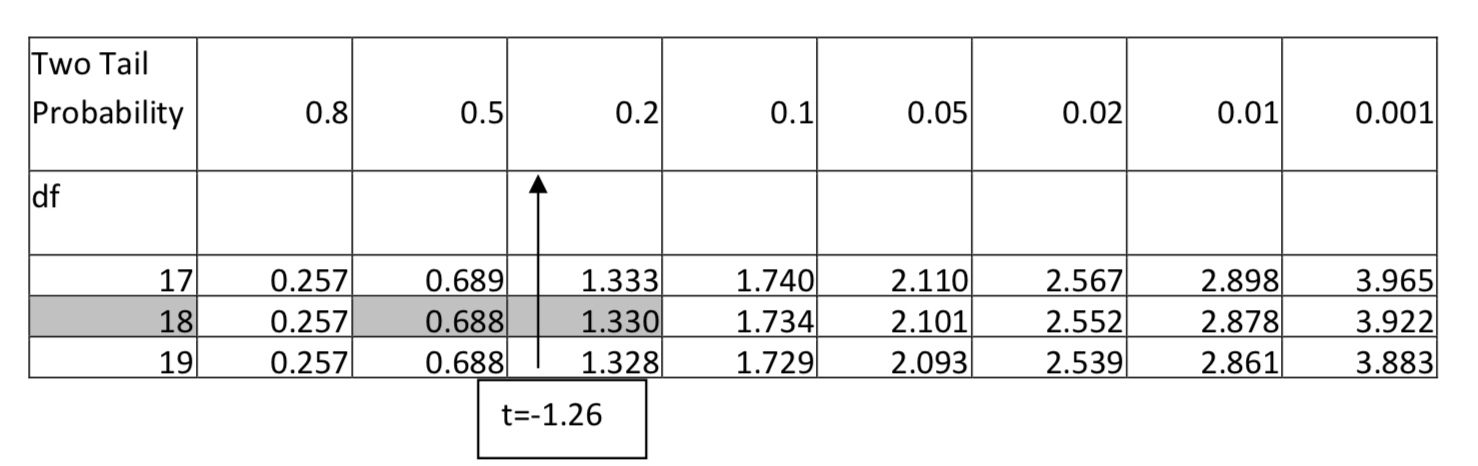
Para 18 grados de libertad, -1.26 cae entre 0.688 y 1.328 si se ignora el signo negativo, por lo que el área en dos colas cae entre 0.5 y 0.2. Dado que cualquier valor en este rango no sería significativo en el nivel 0.01, entonces el valor p es mayor que 0.01. Sin embargo, se puede proporcionar mayor detalle indicando que el valor p es mayor que 0.2. Sería incorrecto decir que el valor p es menor que 0.5 porque eso no nos dice si es mayor o menor que 0.01.
Hay dos enfoques inferenciales diferentes que se pueden tomar. A lo largo de la mayor parte de este texto se ha centrado en el concepto de probar hipótesis. Eso significa que en realidad hay una hipótesis de lo que se encontraría de un censo. El enfoque inferencial alternativo ocurre cuando no hay hipótesis. En tales casos el objetivo es estimar el parámetro en lugar de determinar si la hipótesis al respecto es correcta. Debido a que todo el enfoque del libro ha estado en probar hipótesis, comenzaremos ahí y luego abordaremos la idea de estimar el parámetro en el siguiente capítulo. Hay un número considerable de situaciones de prueba de hipótesis y fórmula, pero nos centraremos en sólo cuatro de ellas en este capítulo y luego agregaremos algunas más en capítulos posteriores. La explicación se proporcionará con una discusión de ejercicio.
Briefing 5.1 Ejercicio
El gobierno de Estados Unidos recomienda que las personas realicen 2.5 horas de ejercicio aeróbico moderadamente intenso cada semana o 1.25 horas de ejercicio vigoroso-intenso cada semana junto con algunos entrenamientos de fuerza como pesas o flexiones. El ejercicio ayuda a reducir el riesgo de diabetes, enfermedades cardíacas, algunos tipos de cáncer y mejora la salud mental. (www.cbsnews.com/8301-204_162-... nded-ejercicio/)
Con estas cinco preguntas se ilustrarán las cuatro fórmulas hipotésis-test que se mostrarán en este capítulo. A medida que leas las preguntas, trata de determinar cualquier similitud o diferencia entre ellas, ya que eso finalmente te guiará hacia qué fórmula se debe usar.
- ¿La proporción de personas que hacen ejercicio es suficiente para cumplir con la recomendación del gobierno menos de 0.25?
- ¿La proporción de personas con un problema de salud como diabetes, enfermedades cardíacas o cáncer es menor para quienes cumplen con la recomendación de ejercicio del gobierno que para quienes no?
- ¿La cantidad promedio de ejercicio que hace un estudiante universitario en una semana es mayor a 2.5 horas?
- ¿El peso promedio de una persona es menor después de un mes de nuevo programa regular de acondicionamiento físico aeróbico?
- Para quienes hacen ejercicio regularmente, ¿la cantidad promedio de ejercicio que hace un egresado universitario en una semana es diferente a alguien que no se gradúa de la universidad?
Hay dos cosas diferentes a buscar a la hora de determinar similitudes y diferencias. El primero es si el parámetro que se menciona es una media o proporción. El segundo es el número de poblaciones. En la siguiente tabla se reafirman las preguntas, se proporciona el parámetro de interés, el número de poblaciones y un ejemplo de las hipótesis.
|
Pregunta |
Parámetro |
Poblaciones |
Hipótesis |
|
¿La proporción de personas que hacen ejercicio es suficiente para cumplir con la recomendación del gobierno menos de 0.25? |
proporción |
1 |
H0:P=0.25 |
|
¿La proporción de personas con un problema de salud como diabetes, enfermedades cardíacas o cáncer es menor para quienes cumplen con la recomendación de ejercicio del gobierno que para quienes no? |
proporción |
2 |
H0:Pexercise=Pdon’t |
|
¿La cantidad promedio de ejercicio que hace un estudiante universitario en una semana es mayor a 2.5 horas? |
media |
1 |
H0:μ=2.5 |
|
¿El peso promedio de una persona es menor después de un mes de nuevo programa regular de acondicionamiento físico aeróbico? |
media |
1 |
H0:μ=0 |
|
Para quienes hacen ejercicio regularmente, ¿la cantidad promedio de ejercicio que hace un egresado universitario en una semana es diferente a alguien que no se gradúa de la universidad? |
media |
2 |
H0:μcollege grad=μnot college grad |
Se necesitarán datos categóricos para preguntas sobre una proporción; se necesitarán datos cuantitativos para preguntas sobre una media. Se necesita una breve explicación para la cuarta cuestión. Para determinar la cantidad de cambio en una persona después de iniciar un programa de acondicionamiento físico, es necesario recolectar dos conjuntos de datos. La persona deberá ser pesada antes del programa de acondicionamiento físico y luego nuevamente después de un mes. Estos datos son dependientes, lo que significa que tienen que aplicar a la misma persona. En definitiva, los datos que se analizarán son la diferencia entre el peso del antes y el después de una persona. Por lo tanto, dos valores de datos se comprimen en un valor por resta. Si la diferencia de peso después de menos antes es 0, entonces no ha habido ningún cambio. Si es menor a 0, se ha perdido peso.
Dado que la evidencia para ayudar a decidir qué hipótesis es apoyada por los datos provendrá de una muestra, y esa muestra es solo uno de los muchos resultados de muestra posibles que forman una distribución de muestreo normalmente distribuida, entonces podemos usar lo que se sabe sobre la distribución de muestreo para determinar la probabilidad que hubiéramos seleccionado los datos que obtuvimos, o datos más extremos (valor p).
A pesar de la naturaleza teórica de una distribución muestral, es la fuente para determinar las probabilidades. Por lo tanto, primero definiremos qué contienen las distribuciones y las fórmulas importantes relacionadas con esta distribución.
La primera vez que encontramos la distribución normal fue cuando se utilizó como aproximación para la distribución binomial. En este caso los datos consistieron en recuentos.
La media de esta distribución se encuentra a partir deμ=np. La desviación estándar esσ=√npq. La fórmula para determinar el número de desviaciones estándar a partir de la media es un valorz=x−μσ.
Los recuentos finalmente se convirtieron en proporciones dividiendo los recuentos por el tamaño de la muestra. La distribución consistió en todas las proporciones de muestra posibles.
La distribución de las proporciones muestrales tiene una media deμˆp=p y una desviación estándar deσˆp=p(1−p)n. La fórmula para determinar el número de desviaciones estándar una proporción muestral es a partir de la media esz=ˆp−p√p(1−p)n.
La siguiente vez que nos encontramos con la distribución normal fue cuando teníamos datos cuantitativos en cuyo caso la distribución estaba compuesta por medias muestrales.
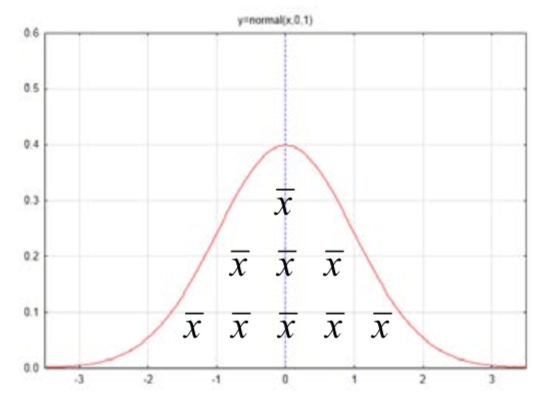
La media de todas las medias de muestra posibles esμˉx=μ y el error estándar esσˉx=σ√n. La fórmula para determinar el número de desviaciones estándar que es una media muestral a partir de la media poblacional hipotética esz=ˉx−μσ√n. Debido a que noσ se conoce, se estima con s, de manera que el error estándar estimado essˉx=s√n y la fórmula Z se sustituye por la fórmula t dondet=ˉx−μs√n.
Las distribuciones y fórmulas que acaban de mostrarse son las mismas o similares a las que usted vio en el Capítulo 5 y que son apropiadas para las preguntas 1, 3 y 4. Por otro lado, las preguntas 2 y 5 tienen hipótesis distintas a las encontradas anteriormente y por lo tanto es necesario un esfuerzo para definir las distribuciones relevantes y sus medias y desviaciones estándar. Estos se basarán en tres resultados estadísticos que no se probarán aquí:
1. La media de la diferencia de dos variables aleatorias es la diferencia de las medias.
2. La varianza de la diferencia de dos variables aleatorias independientes es la suma de las varianzas.
3. La diferencia de dos variables aleatorias independientes normalmente distribuidas también se distribuye normalmente. (Aliaga, Martha y Brenda Gunderson. Estadísticas Interactivas. Upper Saddle River, NJ: Pearson Prentice Hall, 2006. Imprimir.)
Comenzaremos con la pregunta de si la proporción de personas con un problema de salud como diabetes, cardiopatías o cáncer es menor para quienes cumplen con la recomendación de ejercicio del gobierno que para quienes no lo hacen, lo que significa que hay dos poblaciones, la población que ejerce arriba niveles recomendados por el gobierno y la población que no. Dentro de cada población, se encontrará la proporción de personas con un problema de salud. Se utilizará una prueba de hipótesis para determinar si las personas que hacen ejercicio en los niveles recomendados tienen menos problemas de salud que las personas que no lo hacen.
H0:Pexercise=Pdon't
H1:Pexercise<Pdon't
Escribir hipótesis de esta manera es fácil de interpretar, pero una manipulación algebraica de éstas nos dará una idea de la distribución que se utilizaría para representar la hipótesis nula. Pdon’tse restarán de ambos lados.
H0:Pexercise−Pdon't=0
H1:Pexercise−Pdon't<0
Dado que ningunoPexercise oPdon’t se sabe porque estos son parámetros, lo mejor que se puede hacer es estimarlos usando proporciones de muestra. Por lo tanto seˆpexercise utilizará como estimación dePexercise y seˆpdon′t utilizará como estimación dePdon’t. Entoncesˆpexercise−ˆpdon′t como estimación paraPexercise−Pdon’t.
La distribución de interés para nosotros es la que consiste en la diferencia entre proporciones de muestra, genéricamente mostrada comoˆpA−ˆpB.
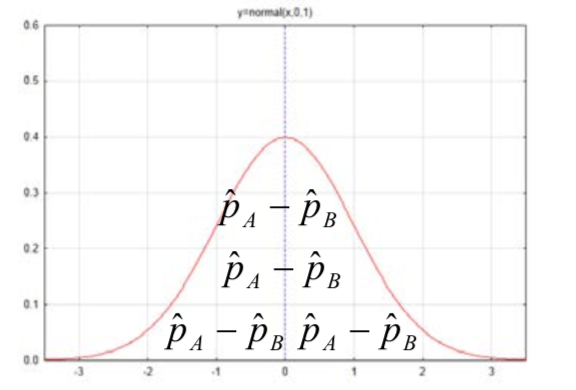
La media de esta distribución espA−pB y la desviación estándar es√pA(1−pA)nA+pB(1−pB)nB. Dado que lo único que se sabepA ypB es que son iguales, es necesario estimar su valor para que realmente se pueda calcular la desviación estándar. Para ello, se combinarán las proporciones muestrales. La proporción combinada se define como
ˆpc=xA+xBnA+nB.
SustituciónpA ypB conˆpc resultados en la fórmula para el error estándar estimado de
√ˆpc(1−ˆpc)nA+ˆpc(1−ˆpc)nB or √ˆpc(1−ˆpc)(1nA+1nB)
Ahora podemos sustituir en laz fórmula,z=x−μσ para obtener el estadístico de prueba utilizado al probar la diferencia entre dos proporciones de población,
z=(ˆpA−ˆpB)−(pA−pB)√ˆpc(1−ˆpc)(1nA+1nB)
Esto se puede escribir un poco más simple en los casos en que la hipótesis nula esPA=PB lo que significa esopA–pB=0, para que ese término pueda ser eliminado para dar el estadístico de prueba
z=(ˆpA−ˆpB)√ˆpc(1−ˆpc)(1nA+1nB)
Para este estadístico de prueba, ambos tamaños de muestra deben ser suficientemente grandes (n>20) con un mínimo de 5 éxitos y 5 fracasos.
Se tomará un enfoque similar con la pregunta 4, que pregunta si la cantidad promedio de ejercicio que hace un egresado universitario en una semana es diferente a alguien que no se gradúa de la universidad? Se comparan dos poblaciones, la población de egresados universitarios y la población de egresados no universitarios. Se comparará la cantidad promedio de ejercicio en cada una de estas poblaciones.
Cuando se comparan las medias de dos poblaciones, las hipótesis se escriben como:
H0:μcollege grad=μnot college grad
H1:μcollege grad≠μnot college grad
Escribir hipótesis de esta manera es fácil de interpretar, pero una manipulación algebraica de éstas nos dará una idea de la distribución que se utilizaría para representar la hipótesis nula.
μnot college gradse restarán de ambos lados.
H0:μcollege grad−μnot college grad=0
H1:μcollege grad−μnot college grad≠0
Ya quen cualquieraμcollege grad oμnot college grad son conocidos porque estos son parámetros, lo mejor que se puede hacer es estimarlos usando medias de muestra. Por lo tanto seˉxcollege grad utilizará como estimación deμcollege grad y seˉxcollege grad utilizará como estimación deμnot college grad. Entoncesˉxcollege grad−ˉxnot college grad
La distribución de interés para nosotros es la que consiste en la diferencia entre medias muestrales, genéricamente mostradas comoˉxA−ˉxB.
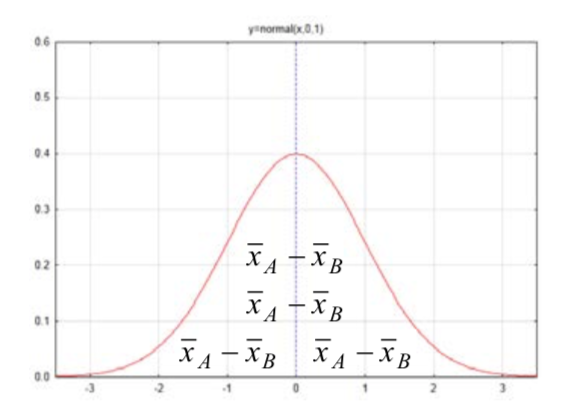
La media de esta distribución esμA−μB y la desviación estándar es√σ2AnA+σ2BnB. Una vez más nos encontramos con el problema de que la desviación estándar de las poblacionesσA y noσB se conocen, por lo que deben estimarse con la desviación estándar muestral sA y sB. Un problema adicional es que no se sabe si las varianzas para las dos poblaciones son iguales (homogéneas). Las varianzas desiguales (heterogéneas) aumentan la tasa de error de Tipo I. (Sheskin, David J. Manual de Procedimientos Estadísticos Paramétricos y No Paramétricos. Boca Ratón: Chapman & Hall/CRC, 2000. Imprimir.)
Se utiliza lat Prueba para Dos Muestras Independientes para probar la hipótesis. Esta prueba depende de los siguientes supuestos.
- Cada muestra se selecciona aleatoriamente de la población que representa.
- La distribución de los datos en la población de la que se extrajo la muestra es normal
- Las varianzas de las dos poblaciones son iguales. Esta es la hipótesis de homogeneidad de varianza. (Sheskin, David J. Manual de Procedimientos Estadísticos Paramétricos y No Paramétricos. Boca Ratón: Chapman & Hall/ CRC, 2000. Imprimir.)
El estadístico de prueba sigue el mismo patrón básico que las otras pruebas, lo que implica encontrar el número de errores estándar que un estadístico está lejos del parámetro hipotético.
t=(ˉxA−ˉxB)−(μA−μB)√s21n1+s22n2
El supuesto con esta fórmula es que los dos tamaños de muestra son iguales. Si se usa esta fórmula cuando los tamaños de muestra no son iguales, hay una mayor probabilidad de cometer un error de Tipo I. En tales casos, se utiliza una fórmula alternativa que incluye el promedio ponderado de las varianzas poblacionales estimadas de los dos grupos. El promedio ponderado se basa en el número de grados de libertad en cada muestra. Esta fórmula se puede utilizar para tamaños de muestra iguales y no iguales.
t=(ˉxA−ˉxB)−(μA−μB)√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB]
Debido a que dos parámetros (σAyσB) son reemplazados porsA ysB, se pierden dos grados de libertad. Así, el número de grados de libertad para este estadístico de prueba esn1+n2−2.
En este capítulo se presentan cuatro pruebas de hipótesis diferentes. Las hipótesis y los estadísticos de las pruebas se resumen en la siguiente tabla.
| Proporciones (para datos categóricos) | Medios (para datos cuantitativos) | |
| 1 - muestra | H0:p=p0 H1:p<p0op>p0 op≠p0 z=ˆp−p√p(1−p)n Supuestos: np≥5,n(1−p)≥5 |
H0:μ=μ0 H1:μ<μ0μ>μ0oμ≠μ0 t=ˉx−μs√n df = n - 1 Supuestos: Sin<30, la población está aproximadamente distribuida normalmente. |
| 2 - muestras | H0:pA=pB H1:pA<pBopA>pB opA≠pB z=(ˆpA−ˆpB)−(pA−pB)√ˆpc(1−ˆpc)(1nA+1nB) dondeˆpc=xA+xBnA+nB Supuestos: np≥5,n(1−p)≥5 para ambas poblaciones |
H0:μA=μB H1:μA<μBμA>μBoμA≠μB t=(ˉxA−ˉxB)−(μA−μB)√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB] df =nA+nB−2 Supuestos: Sin<30, la población está aproximadamente distribuida normalmente. |
Para cada situación de prueba de hipótesis, tendrás que decidir qué fórmula y qué tabla usar. Observe que cuando las hipótesis son sobre proporciones, se utiliza laz distribución normal estándar. Cuando las hipótesis son sobre medias, se utilizan las distribuciones t.
Ahora volveremos a nuestras cinco preguntas originales. Las estadísticas dadas en este problema son ficticias.
- ¿La proporción de personas que hacen ejercicio es suficiente para cumplir con la recomendación del gobierno menos de 0.25?
Supongamos que se tomó una muestra aleatoria de 800 adultos. De estos, 184 aseguraron que cumplieron con la recomendación de ejercicio del gobierno. ¿Podemos concluir que la proporción que cumple con esta recomendación es menor al 25%? Utilizar un nivel de significancia de 0.05.
Las hipótesis son:
H0:p=0.25
H1:p<0.25
La proporción muestral esˉp=xn=184800=0.23
El estadístico de prueba esz=ˆp−p√p(1−p)n. Con sustituciónz=0.23−0.25√0.25(1−0.25)800=−1.31
Consulte la tabla de distribución normal estándar para encontrar el área a la izquierda es de 0.0951. Este es el valor p porque la dirección del extremo es hacia la izquierda. Dado que el valor p es mayor que el nivel de significancia, los datos son consistentes con la hipótesis nula. Se concluye que en el nivel 0.05 de significancia, la proporción de adultos que cumplen con las recomendaciones del gobierno para el ejercicio no es significativamente menor al 25% (z= -1.31,p = 0.0951,n = 800). - ¿La proporción de personas con un problema de salud como diabetes, enfermedades cardíacas o cáncer es menor para quienes cumplen con la recomendación de ejercicio del gobierno que para quienes no?
Supongamos que se toma una muestra aleatoria de ambas poblaciones. Para las personas que cumplen con la cantidad recomendada de ejercicio, 84 de 560 tuvieron un problema de salud. Para las personas que no hicieron suficiente ejercicio, 204 de 850 tenían un problema de salud.
Las hipótesis son:
H0:Pexercise=Pdon't
H1:Pexercise<Pdon't
Las proporciones muestrales sonˆpexercise=xn=84560=0.15 yˆpdon′t=xn=204850=0.24
La proporción agrupada es ˆpc=xA+xBnA+nB=84+204560+850=0.204
El estadístico de prueba esz=(ˆpA−ˆpB)−(pA−pB)√ˆpc(1−ˆpc)(1nA+1nB)
con sustituciónz=(0.15−0.24)√0.204(1−0.204)(1560+1850)=−4.10
Comprobando la tabla de distribución normal estándar, elz valor de -4.10 está por debajo del valor más bajo en la tabla (-3.49) por lo tanto el área en la cola izquierda es menor a 0.0002. Se concluye que en el nivel 0.05 de significancia, la proporción de problemas de salud para las personas que cumplen con la recomendación del gobierno para hacer ejercicio es significativamente menor que para las personas que no hacen tanto ejercicio (z= -4.10, p < 0.0002,nexercise=560,ndon’t=850). - ¿La cantidad promedio de ejercicio que hace un estudiante universitario en una semana es mayor a 2.5 horas?
Para esta pregunta, la evidencia que hay que reunir son horas de ejercicio en una semana. Eso es datos cuantitativos. Para usar la prueba t, necesitamos asegurarnos de que los datos en la muestra estén aproximadamente distribuidos normalmente. Las hipótesis que se probarán son:
H0:μ=2.5
H1:μ>2.5
El nivel de significancia es 0.10.
El número de horas de ejercicio por 20 estudiantes seleccionados al azar se muestra en la siguiente tabla.3.7 2 7.1 1.7 0 0 2.1 2.9 4 3.2 3.4 1.3 1 4.2 0 1.3 2.9 5.3 4.4 2.3 Un histograma para estos datos muestra que se distribuye aproximadamente normalmente. La mayor desviación de la normalidad se encuentra en la cola izquierda ya que no es posible hacer ejercicio menos de 0 horas a la semana.
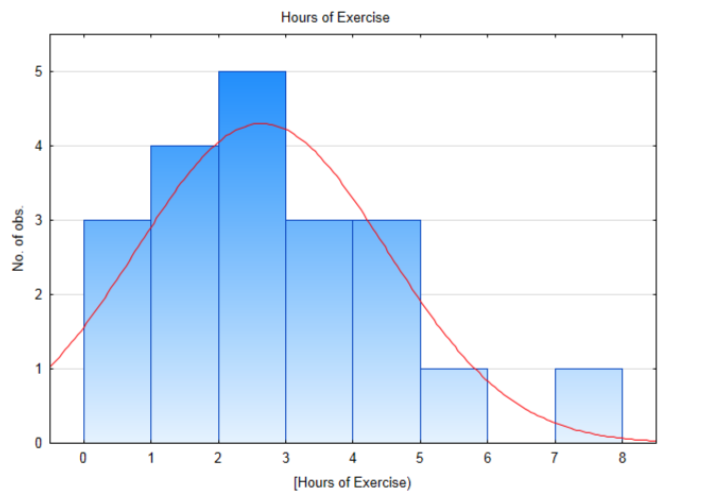
La media de la muestra y la desviación estándar son 2.64 horas y 1.855 horas, respectivamente. El estadístico de prueba es:t=ˉx−μs√n, con sustitución,t=2.64−2.51.855√20. Después de la simplificación, t = 0.338. Hay 19 grados de libertad (20 — 1). Usa la tabla t, en la fila con 19 grados de libertad, encuentra la ubicación de 0.338. A continuación se muestra un extracto de la tabla. Observe que 0.338 cae entre 0.257 y 0.688 por lo que consecuentemente la tabla muestra que el área en la cola derecha está entre 0.25 y 0.40. Dado que el nivel de significancia es 0.1, y dado que el área en la cola es mayor que 0.1 y más específicamente mayor que 0.25, reportaríamos que el valor p es mayor que 0.25.
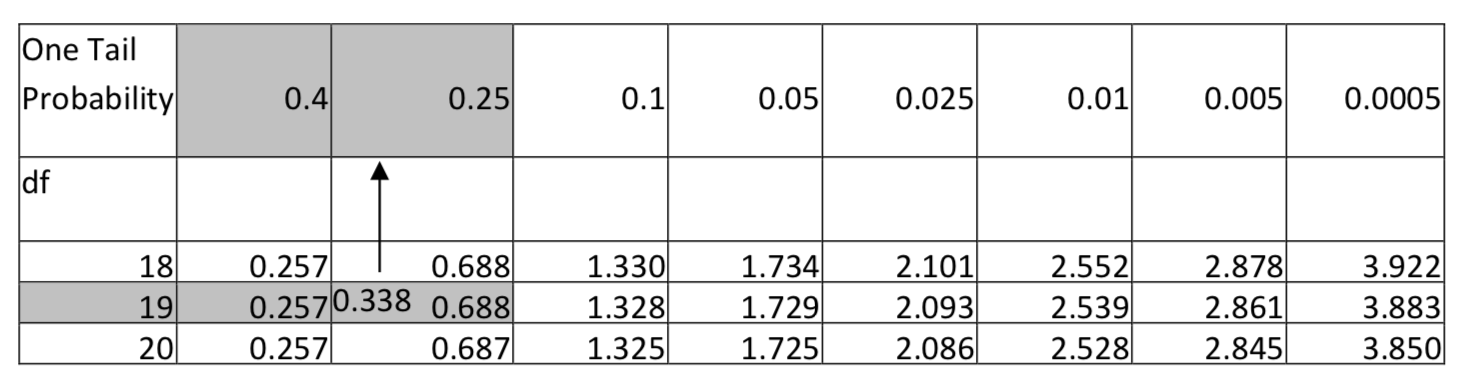
Conclusión: en el nivel de significancia 0.10, el tiempo promedio que los estudiantes universitarios ejercen no es significativamente mayor a 2.5 horas (t= 0.338,p > 0.25,n = 20). - ¿El peso promedio de una persona es menor después de un mes de nuevo programa regular de acondicionamiento físico aeróbico?
Para esta pregunta, se deben recolectar dos conjuntos de datos, el peso antes y el peso después. El peso antes se restará del peso posterior para determinar el cambio de peso. Debido a que en última instancia solo habrá un conjunto de datos, se utilizará la prueba t para una media poblacional.
H0:μ=0
H1:μ<0
El nivel de significancia es 0.10.Sujeto 1 2 3 4 5 6 7 8 9 Antes del peso 158 213 142 275 184 136 172 263 205 Después del peso 154 213 135 278 180 134 171 258 199 Después Antes -4 0 -7 3 -4 -2 -1 -5 -6 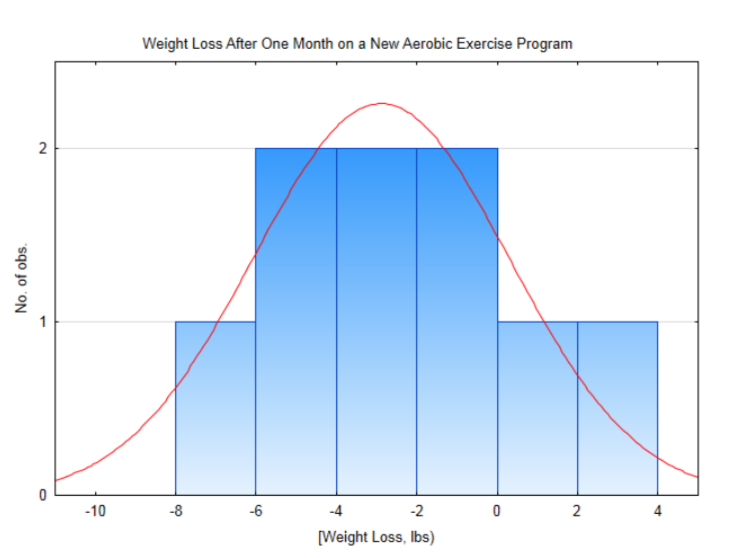
Esta distribución es aproximadamente normal, por lo que es apropiado utilizar la prueba t para una media poblacional. La media muestral es de -2.89 lbs con una desviación estándar de 3.18 lbs El estadístico de prueba es:t=ˉx−μs√n, con sustitución,t=−2.89−03.18√9. Después de la simplificación, t = -2.726. Hay 8 grados de libertad (9-1). Dado que -2.726 cae entre 2.306 y 2.896 en la fila para 8 grados de libertad y dado que el nivel de significancia es 0.1 pero el área en la cola a la izquierda de -2.726 es menor de 0.025, entonces la conclusión es que el nuevo peso es significativamente menor que el peso original (t= -2.726,p < 0.025,n = 9). Concluimos que las personas perdieron peso.
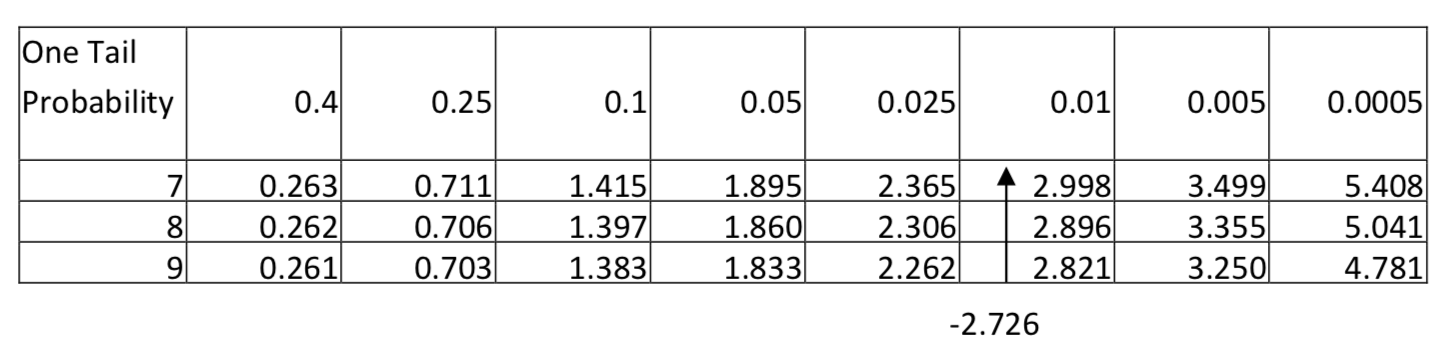
- Para quienes hacen ejercicio regularmente, ¿la cantidad promedio de ejercicio que hace un egresado universitario en una semana es diferente a alguien que no se gradúa de la universidad?
Supongamos que se toma una muestra aleatoria para la población de egresados universitarios que hacen ejercicio regularmente y se toma una muestra aleatoria diferente de la población de no egresados que hacen ejercicio regularmente. También supongamos que la cantidad de ejercicio se distribuye normalmente para ambos grupos y que la varianza es homogénea. A continuación se muestran las hipótesis. Utilizar un nivel de significancia de 0.05.
H0:μcollege grad=μnot college grad
H1:μcollege grad≠μnot college grad
La siguiente tabla muestra la media, la desviación estándar y el tamaño de la muestra para las dos muestras.Unidades: horas/semana Egresados Universitarios Graduaciones no universitarias Media 4.2 3.8 Desviación estándar 1.3 1.2 Tamaño de la muestra,n 12 16 La diferencia en el tamaño de la muestra significa que necesitamos la fórmula estadística de prueba: la
t=(ˉxA−ˉxB)−(μA−μB)√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB]
cual se usa para poblaciones independientes. Sustituir en la fórmula da:
t=(4.2−3.8)−(0)√[(12−1)1.32+(16−1)1.2212+16−2][112+116]=0.842
Debido al signo de desigualdad en la hipótesis alternativa, esta es una prueba de dos colas. El estadístico de prueba de 0.842 produce un valor p entre 0.5 y 0.8. Dado que esto es claramente superior al nivel de significancia, la conclusión es que al nivel 0.05 de significancia, la cantidad de ejercicio para los egresados universitarios no es significativamente diferente a la cantidad para los no egresados (t= 0.842,p > 0.5,ncollege grads=12,nnot college grads=16). 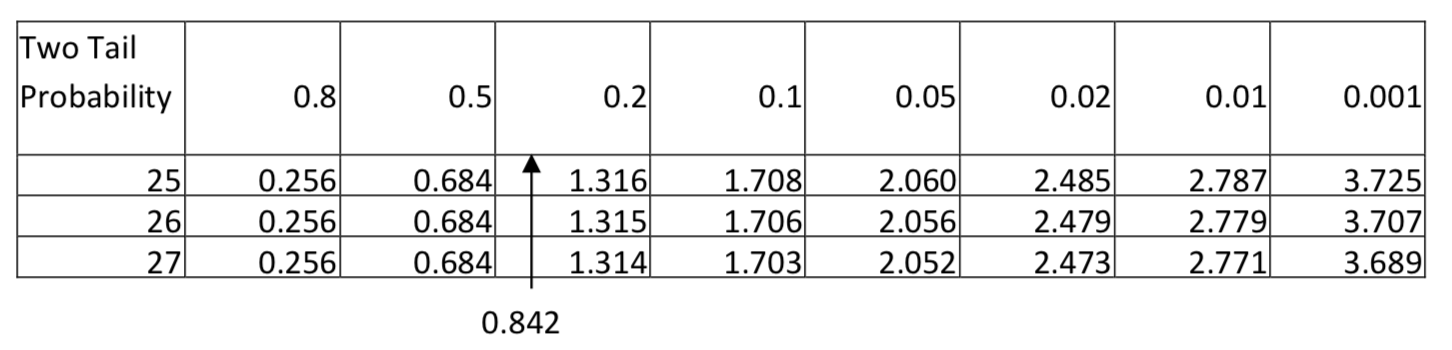
La prueba t para dos muestras independientes se ha basado en el supuesto de homogeneidad de varianza. Existen pruebas para determinar si la varianza es homogénea y modificaciones que se pueden hacer a los grados de libertad si no lo es, estas no están incluidas en este texto.
Todas estas pruebas se pueden hacer usando la calculadora TI84. Las pruebas se encuentran seleccionando la tecla STAT y luego usando las flechas del cursor para desplazarse hacia la derecha a PRUEBAS.
| Proporciones (para datos categóricos) | Medios (para datos cuantitativos) | |
| 1 - muestra | H0:p=p0 H1:p<p0p>p0op≠p0 Prueba 5:1- PropzTest |
H0:μ=μ0 H1:μ<μ0omu>μ0 omu≠μ0 Prueba 2: T- Test |
| 2 - muestras | H0:pA=pB H1:pA<pBopA>pB opA≠pB Prueba 6:2- PropzTest |
H0:μA=μB H1:μA<μBμA>μBoμA≠μB Prueba 4:2-SamptTest |


