10.7: Doble rendija

Esto corresponde a retornar al interferómetro de YoUNG. Por sencillez, vamos a pensar que $\mathbf{k}$ está en el plano $\xi z$ por lo que $k_{y}=0 \mathrm{y} k_{x}=k \sin \theta$ (quitamos una dimensión al problema). Trabajaremos en la aproximación de FRAUNHOFER.

$$\hat{u}\left(x^{\prime}\right) \propto \int t(\xi) u(\xi) e^{-i \frac{k}{f^{\prime}} x^{\prime} \xi} d \xi \notag$$

Figura $\PageIndex{1}$: Doble rendija. $\Sigma$ y $\Sigma^{\prime}$ son las rendijas de altura a (separadas una distancia $d$ ). Se iluminan por una oap que forma un ángulo $\theta$ con el eje. $\theta^{\prime}$ es el ángulo que parametriza el punto de observación en el plano focal imagen $\left(x^{\prime}\right) . z=0$ sobre el plano de las rendijas.

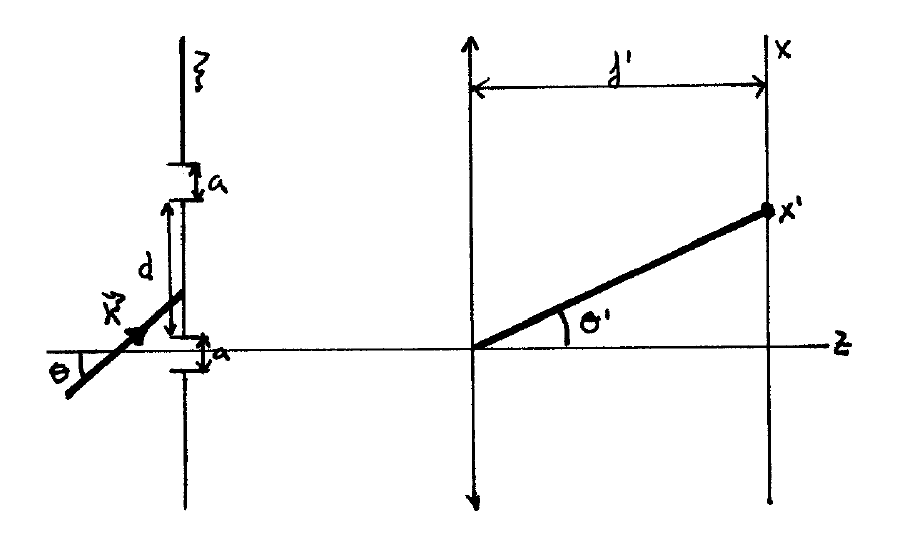
la función transmitancia es $t(\xi)=1$ si $\xi \in \Sigma \cup \Sigma^{\prime}$ y cero en otro caso. En cuanto a la iluminación (segundo dato necesario para usar las fórmulas de $\mathrm{FF}$ ):

$$\begin{aligned} u(\xi) &=u_{0} e^{i \mathbf{k} \cdot \mathbf{r}} \\ &=u_{0} e^{i k_{x} \xi} \\ &=u_{0} e^{i k \sin \theta \xi} \end{aligned}$$

En realidad tenemos dos integrales

$$\hat{u}\left(x^{\prime}\right) \propto \int_{-\frac{a}{2}}^{\frac{a}{2}} e^{i k \sin \theta \xi} e^{-i \frac{k}{f^{\prime}} x^{\prime} \xi} d \xi+\int_{d-\frac{a}{2}}^{d+\frac{a}{2}} e^{i k \sin \theta \xi} e^{-i \frac{k}{f^{\prime}} x^{\prime} \xi} d \xi \notag$$

se pueden reorganizar los términos para extraer conclusiones interesantes. Para que las dos lleven el mismo dominio de integración cambiamos la variable muda en la segunda integral, de modo que el cálculo de una se reduzca al de otra. En efecto, si $\xi^{\prime}=\xi+d y$ operamos

$$\begin{aligned} \hat{u}\left(x^{\prime}\right) \propto & \int_{-\frac{a}{2}}^{\frac{a}{2}} e^{i k \sin \theta \xi} e^{-i k \frac{x^{\prime}}{f^{\prime}} \xi} d \xi \\ &+e^{i\left(k \sin \theta-k \frac{x^{\prime}}{f^{\prime}}\right) d} \int_{-\frac{a}{2}}^{\frac{a}{2}} e^{i\left(k \sin \theta-k \frac{x^{\prime}}{f^{\prime}}\right) \xi} d \xi \end{aligned}$$

(el factor delante de la segunda integral es debido al cambio de variable). Ahora, sacando factor común

$$\hat{u}\left(x^{\prime}\right) \propto\left(1-e^{-i \varphi}\right) \operatorname{sinc}(\phi) \notag$$

Figura $\PageIndex{2}$: Doble rendija. Interpretación de $\varphi$ en el factor interferencial.

donde

$$\begin{aligned} \varphi &=\left(k \frac{x^{\prime}}{f^{\prime}}-k \sin \theta\right) d \\ \phi &=\left(k \frac{x^{\prime}}{f^{\prime}}-k \sin \theta\right) \frac{a}{2} \end{aligned}$$

como en todos los problemas anteriores estamos interesados más bien en la distribución de intensidades

$$\begin{aligned} I\left(x^{\prime}\right) & \propto\left|\hat{u}\left(x^{\prime}\right)\right|^{2} \\ & \propto(1+\cos \varphi) \operatorname{sinc}^{2}(\phi) \end{aligned}$$

1. El primer paréntesis (lo llamamos factor $I_{d}$ porque sólo depende de la separación de las rendijas) se puede identificar como la interferencia de dos ondas con desfase $\varphi$ (era de esperar).

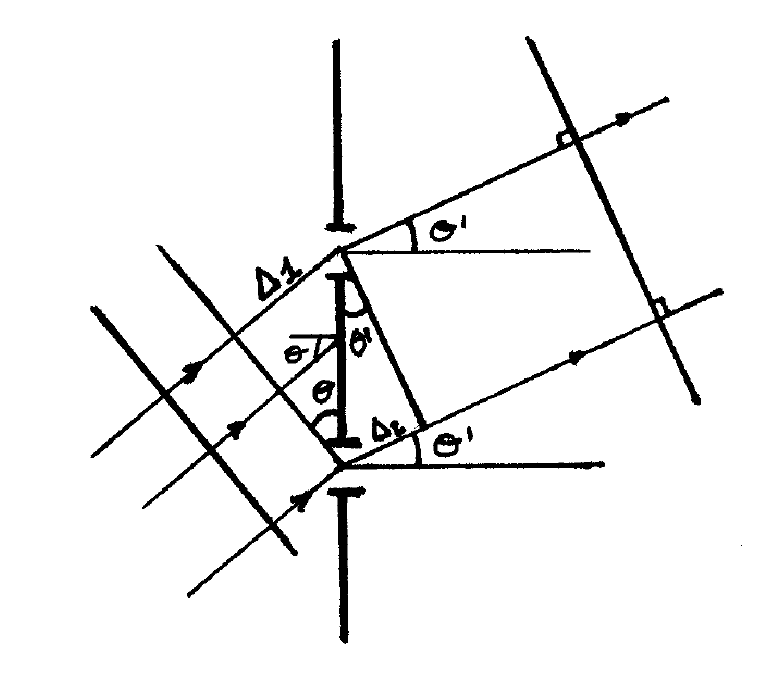
Como se ve en la figura, los rayos que partiendo de la abertura convergen tras pasar por la lente, deben salir de la abertura paralelos entre sí. Hasta ahora el plano focal imagen lo hemos parametrizado mediante $x^{\prime}$. Pero nos va a ser más cómodo hacerlo mediante el ángulo $\theta^{\prime}$, variable que determina el punto de la pantalla cuya intensidad queremos saber (o, dicho de otro modo, la dirección en la que observamos). Para una onda plana las equifases son planos que forman un ángulo $\theta$ con el plano de las aberturas. Siguiendo el razonamiento del $\mathrm{FP}$, la diferencia de camino óptico es $\Delta_{1}-\Delta_{2}$. Con la trigonometría apropiada,

$$\begin{aligned} \sin \theta &=\frac{\Delta_{1}}{d} \\ \sin \theta^{\prime} &=\frac{\Delta_{2}}{d} \end{aligned}$$

Figura $\PageIndex{3}$: Doble rendija. Los dos factores por separado. $\varphi=2 \pi M$ para los máximos de $I_{d}$, que varía más deprisa (ya que $d>a$ ) que la $I_{a}$, para la que el máximo central está en $x^{\prime}=f^{\prime} \sin \theta$ (y vale 1 , nótese la ampliación de los detalles finos a ambos lados del máximo central que hemos efectuado). Se ha utilizado $\varphi=4 \phi$

la diferencia de camino se convierte en diferencia de fase multiplicando por $\frac{2 \pi}{\lambda}$ :

$$\begin{aligned} \varphi &=\frac{2 \pi}{\lambda}\left(\Delta_{2}-\Delta_{1}\right) \\ &=\frac{2 \pi}{\lambda} d\left(\sin \theta^{\prime}-\sin \theta\right) \end{aligned}$$

el objeto de todos estos cálculos es identificar este $\varphi$ con el que aparece en $1+\cos \varphi$, el factor de interferencia. Comparando las expresiones, concluimos que la igualdad entre ambos cálculos exigiría que $\sin \theta^{\prime}=\frac{x^{\prime}}{f^{\prime}}$, cosa que es falsa en general, ya que vemos en la figura que $\frac{x^{\prime}}{f^{\prime}}=\tan \theta^{\prime}$. Pero hay que recordar que el cálculo lo hemos hecho usando la aproximación de FF, que viene de la aproximación paraxial de FRESNEL. Es decir, que si los ángulos $\theta^{\prime}$ son pequeños coinciden el cálculo exacto y el aproximado

$$\sin \theta^{\prime} \simeq \tan \theta^{\prime}=\frac{x^{\prime}}{f^{\prime}} \notag$$

En lo que sigue utilizaremos $\varphi$ en su expresión más exacta (sustituiremos $\frac{x^{\prime}}{f^{\prime}}$ por $\sin \theta^{\prime}$ ), para ampliar el dominio de validez de los cálculos.

2. El segundo factor es la difracción causada por una rendija. Lo llamaremos $I_{a}$, porque sólo depende del tamaño de la rendija.

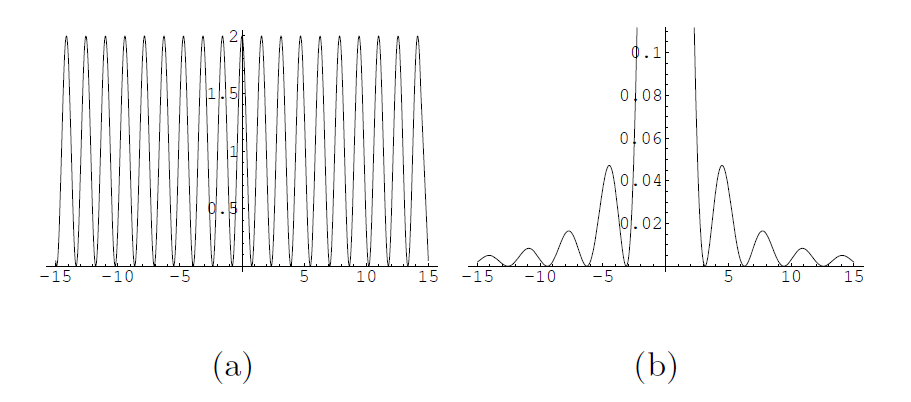
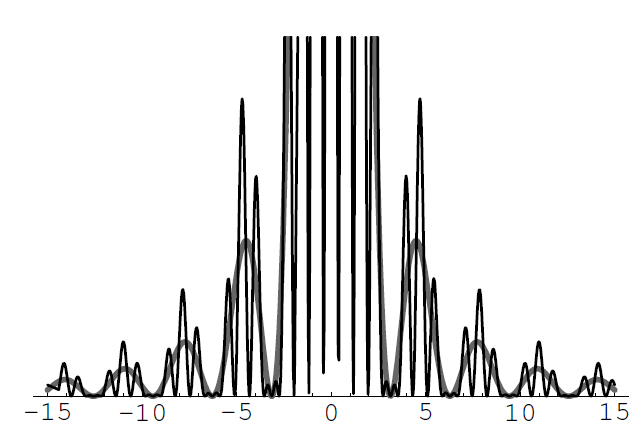
Como vemos, el problema está diseccionado en un factor de interferencia $I_{d}$ y otro de difracción $I_{a}$. El aspecto de cada factor se muestra en la figura 10.21. Como la $I_{d}$ varía más deprisa que la $I_{a}$ podemos considerar que lo que hace esta última es modular la $I_{d}$, como se muestra en la figura 10.22. El término de difracción lo que hace es limitar el número de máximos de interferencia que podemos ver (prácticamente sólo podremos ver los que estén dentro de la campana central).

Figura $\PageIndex{4}$: Doble rendija. $I\left(x^{\prime}\right)=I_{d} \times I_{a}$. El máximo central es el $M=0$ de $I_{d}$. De nuevo se han ampliado los detalles finos a los lados del máximo principal. Se ha utilizado $\varphi=8 \phi$.

Mirando las integrales

$$\begin{aligned} \hat{u}\left(x^{\prime}\right) \propto & \int_{-\frac{a}{2}}^{\frac{a}{2}} e^{i k \sin \theta \xi} e^{-i \frac{k}{f^{\prime}} x^{\prime} \xi} d \xi \\ &+\int_{d-\frac{a}{2}}^{d+\frac{a}{2}} e^{i k \sin \theta \xi} e^{-i \frac{k}{f^{\prime}} x^{\prime} \xi} d \xi \end{aligned}$$

podemos identificar el primer término como $\hat{u}_{1}$ y el segundo como $\hat{u}_{2}$, los términos de difracción de cada una de las rendijas. Al considerar la intensidad vemos que aparece el fenómeno de difracción, puesto que una onda no difiere de la otra más que en la exponencial compleja $e^{-i \varphi}$

$$\hat{u}_{2}=e^{-i \varphi} \hat{u}_{1} \notag$$

Es decir que se dan las condiciones de interferencia puesto que son ondas iguales salvo diferencia de fase.

Si ocultásemos una de las rendijas, se presentaría $I_{1} \propto\left|\hat{u}_{1}\right|^{2}$ o $I_{2} \propto\left|\hat{u}_{2}\right|^{2}$ (en función de cuál tapemos). Pero sabemos que

$$I_{2} \propto\left|\hat{u}_{2}\right|^{2}=\left|\hat{u}_{1}\right|^{2} \notag$$

de donde

$$I_{1}=I_{2}=\operatorname{sinc}^{2} \phi \notag$$

Las distribuciones de intensidades debidas a las rendijas separadamente son iguales. Es decir, en FF, la figura de difracción de una rendija no depende de si está más arriba o más abajo en el el plano de las aberturas. Lo único que cambia es la fase que separa a las ondas. Mover la rendija no desplaza la figura de difracción. Ambas ondas comparten el factor de difracción. Se solapan sobre la pantalla, sólo distintas por la fase.

Al separar mucho las rendijas se acaba perdiendo la interferencia, ya que desaparece la condición necesaria de coherencia espacial entre las dos ondas. Obsérvese que no por utilizar incidencia normal se pierde la inteferencia, ya que el desfase entre las dos ondas tiene dos términos:

Figura $\PageIndex{1}$: Red de difracción de $N$ rendijas de anchura $a$.

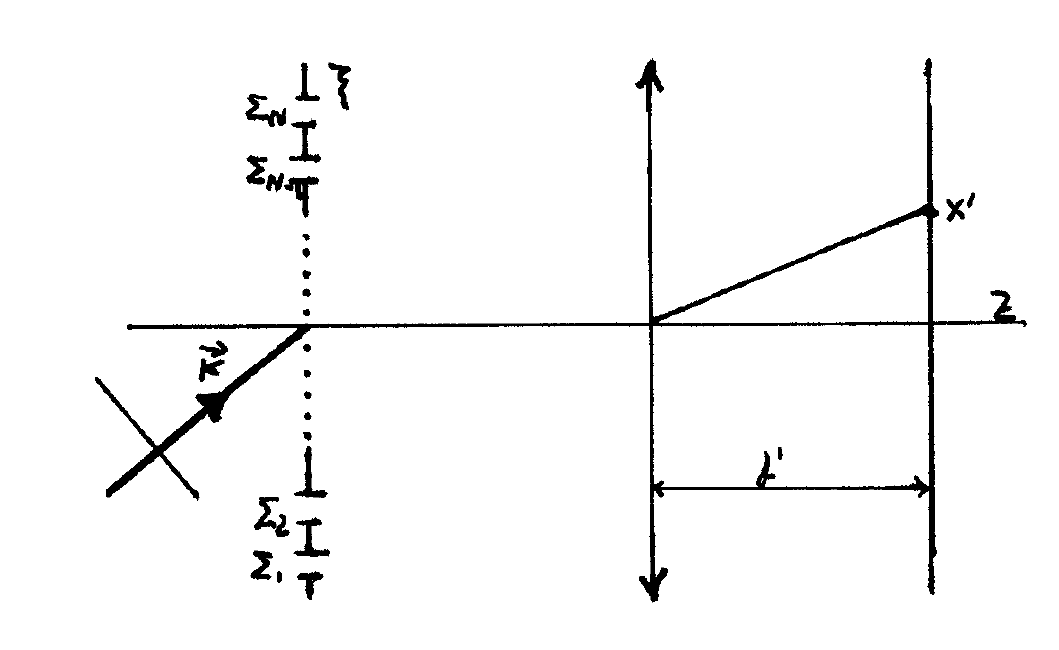
1. lo que las ondas llevan de desfase al llegar al plano de las aberturas, que, como depende de $\sin \theta$, se hace cero cuando la incidencia es normal.
2. lo que acumulan al llegar desde diferentes puntos del plano de las aberturas al plano de la imagen, que no depende de si la incidencia es normal o no.