2.5: Secciones Cónicas
- Page ID
- 130950
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hasta ahora hemos definido una elipse, una parábola y una hipérbola sin ninguna referencia a un cono. Muchos lectores sabrán que una sección plana de un cono es o bien una elipse, una parábola o una hipérbola, dependiendo de si el ángulo que hace el plano con la base del cono es menor que, igual o mayor que el ángulo que el generador del cono hace con su base. No obstante, dadas las definiciones de elipse, parábola e hipérbola que hemos dado, se requiere prueba de que en realidad son secciones cónicas. También se podría mencionar en este punto que una sección plana de un cilindro circular es también una elipse. También, por supuesto, si el plano es paralelo a la base del cono, o perpendicular al eje del cilindro, la elipse se reduce a un círculo.
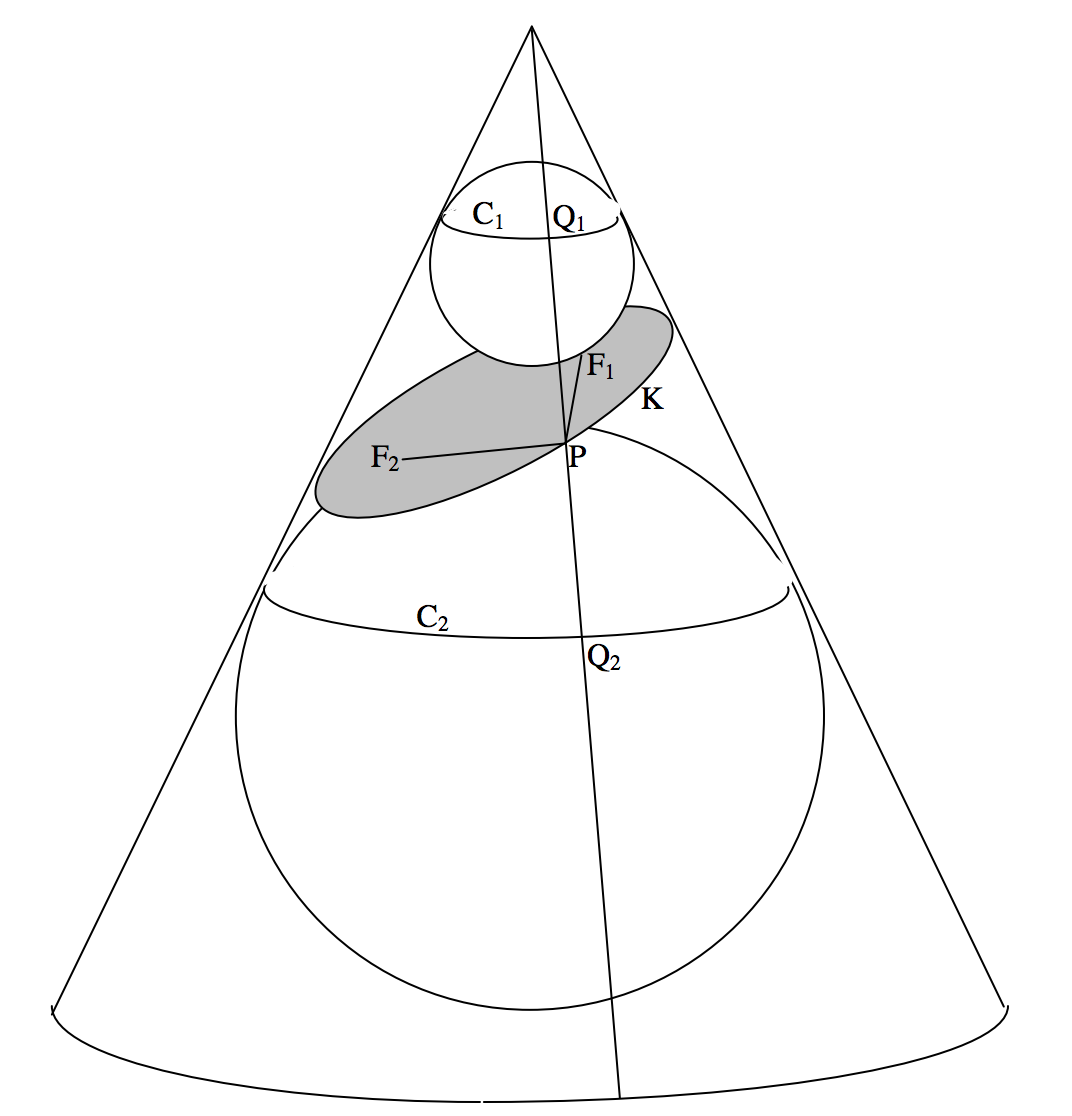
\(\text{FIGURE II.36}\)
Una prueba sencilla y notable se puede dar en el clásico euclidiano “Dado. Requerido. Construcción. Comprobante. Estilo Q.E.D.”.
Prueba
Dado: Un cono y un plano tal que el ángulo que hace el plano con la base del cono es menor que el ángulo que hace el generador del cono con su base, y el plano corta el cono en una curva cerrada\(\text{K}\). Figura\(\text{II.36}\).
Requerido: Para probar que\(\text{K}\) es una elipse.
Construcción: Construir una esfera por encima del plano, que toque el cono internamente en el círculo\(\text{C}_1\) y el plano en el punto\(\text{F}_1\). Construye también una esfera debajo del plano, que toque el cono internamente en el círculo\(\text{C}_2\) y el plano en el punto\(\text{F}_2\).
Unir un punto\(\text{P}\) en la curva\(\text{K}\) hacia\(\text{F}_1\) y hacia\(\text{F}_2\).
Dibuja el generador que pasa por el punto\(\text{P}\) y que se cruza\(\text{C}_1\) en\(\text{Q}_1\) y\(\text{C}_2\) en\(\text{Q}_2\).
Prueba:\(\text{PF}_1 = \text{PQ}_1\) (Tangentes a una esfera desde un punto externo.)
\(\text{PF}_2 = \text{PQ}_2\)(Tangentes a una esfera desde un punto externo.)
\(\therefore \text{PF}_1 + \text{PF}_2 = \text{PQ}_1 + \text{PQ}_2 = \text{Q}_1 \text{Q}_2\)
y\(\text{Q}_1\text{Q}_2\) es independiente de la posición de\(\text{P}\), ya que es la distancia entre los círculos\(\text{C}_1\) y\(\text{C}_2\) medida a lo largo de un generador.
\[\therefore \ \text{K is an ellipse and } \text{F}_1 \text{ and } \text{F}_2 \text{ are its foci}. \tag{Q.E.D.}\]
Un argumento similar mostrará que una sección plana de un cilindro también es una elipse.
El lector también puede idear dibujos que mostrarán que una sección plana de un cono paralelo a un generador es una parábola, y que un plano más empinado que un generador corta el cono en una hipérbola. Los dibujos son más fáciles de hacer con papel, lápiz, brújula y regla, y requerirán algo de ingenio. Si bien he visto la prueba anterior para una elipse en varios libros, no he visto las pruebas correspondientes para una parábola y una hipérbola, pero sí se pueden hacer, y el lector debería encontrarle un reto interesante. Si el lector puede usar una computadora para hacer los dibujos y puede hacerlo mejor que mi pobre esfuerzo con la figura\(\text{II.36}\), es bastante bueno con una computadora, lo cual es una señal de una juventud mal gastada.