1.2: Posición, Desplazamiento, Velocidad

La cinemática es la parte de la mecánica que se ocupa de la descripción matemática del movimiento, dejando de lado la cuestión de qué causa que un objeto se mueva de cierta manera. La cinemática, por lo tanto, no incluye cosas como las fuerzas o la energía, que en cambio caen bajo el epígrafe de la dinámica. Se puede decir, entonces, que la cinemática por sí misma no es verdadera física, sino solo matemática aplicada; sin embargo, sigue siendo una parte esencial de la mecánica clásica, y su punto de partida más natural. Este capítulo (y partes del siguiente) introducirá los conceptos y métodos básicos de la cinemática en una dimensión.

Posición

Como se indicó en el apartado anterior, inicialmente nos interesa únicamente describir el movimiento de una “partícula”, que puede considerarse como un punto matemático en el espacio. (Más adelante veremos que, incluso para un objeto o sistema extendido, a menudo es útil considerar el movimiento de un punto específico que llamamos centro de masa del sistema). Un punto en tres dimensiones se puede ubicar dando tres números, conocidos como sus coordenadas cartesianas (o, más simplemente, sus coordenadas). En dos dimensiones, esto funciona como se muestra en la Figura\(\PageIndex{1}\) a continuación. Como puedes ver, las coordenadas de un punto solo nos dicen cómo encontrarlo moviendo primero una cierta distancia\(x\), desde un origen previamente acordado, a lo largo de un eje horizontal (o\(x\)), y luego una cierta distancia\(y\) a lo largo de un eje vertical (o\(y\)). (O, por supuesto, igualmente bien podrías primero moverte verticalmente y luego horizontalmente).

Figura\(\PageIndex{1}\): El vector de posición\( \vec r\),, de un punto,\(x\) y sus\(y\) componentes (las coordenadas del punto).

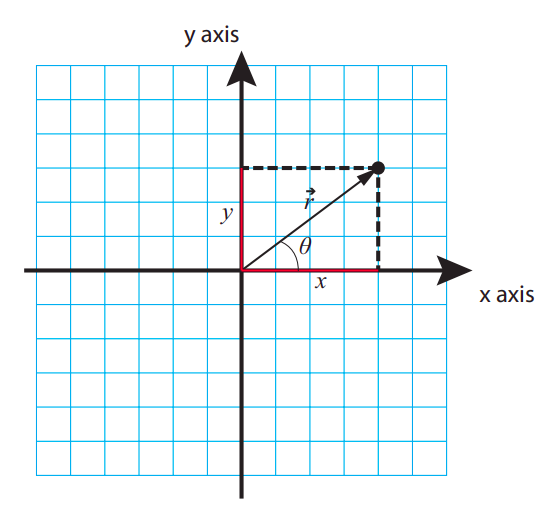
Las cantidades\(x\) y\(y\) se toman para ser positivas o negativas dependiendo de qué lado del origen se encuentre el punto. Normalmente, siempre comenzaremos eligiendo una dirección positiva para cada eje, ya que la dirección a lo largo de la cual aumenta el valor algebraico de la coordenada correspondiente. Esto a menudo se elige para estar a la derecha para el eje horizontal, y hacia arriba para el eje vertical, pero no hay nada que diga que no podemos elegir una convención diferente si resulta ser más conveniente. En la Figura\(\PageIndex{1}\), las flechas en los ejes denotan la dirección positiva para cada uno. Pasando por la cuadrícula, las coordenadas del punto mostrado son\(x\) = 4 unidades,\(y\) = 3 unidades.

En dos o tres dimensiones (e incluso, en cierto sentido, en una dimensión), las coordenadas de un punto pueden interpretarse como los componentes de un vector que llamamos vector de posición del punto, y denotan por\(\vec r\) (a veces se usan letras negritas para vectores, en lugar de una flecha en top; en ese caso, el vector de posición sería denotado por r). Un vector es un objeto matemático, con propiedades geométricas y algebraicas específicas, que los físicos utilizan para representar una cantidad que tiene tanto una magnitud como una dirección. La magnitud del vector de posición en la Figura\(\PageIndex{1}\) es solo la longitud de la flecha, es decir, 5 unidades de longitud (según el teorema de Pitágoras, la longitud de\(\vec r\), que a menudo escribiremos usando barras de valor absoluto como\(|\vec{r}|\), es igual a\( \sqrt{x^{2}+y^{2}} \)); esto es solo la recta -línea distancia del punto al origen. La dirección de\(\vec r\), por otra parte, se puede especificar de varias maneras; una convención común es dar el valor del ángulo que hace con el\(x\) eje positivo, que he denotado en la figura como\(\theta\) (en este caso, se puede verificar que\( \theta=\tan ^{-1}(y / x)=36.9^{\circ} \)). En tres dimensiones, se necesitarían dos ángulos para especificar completamente la dirección de\(\vec r\).

Como se puede ver, dar la magnitud y dirección de\(\vec r\) es una manera de ubicar el punto que es completamente equivalente a dar sus coordenadas\(x\) y\(y\). De la misma manera, las coordenadas\(x\) y\(y\) son una forma de especificar el vector\(\vec r\) que es completamente equivalente a dar su magnitud y dirección. Como dije anteriormente, llamamos a x e y a los componentes (o a veces, para ser más específicos, los componentes cartesianos) del vector\(\vec r\). En cierto sentido todos los vectores que se introducirán más adelante en este semestre derivarán sus propiedades geométricas y algebraicas a partir del vector de posición\(\vec r\), así que una vez que sepas tratar con un vector, podrás lidiar con todos ellos. Las propiedades geométricas (por lo que quiero decir, cómo relacionar los componentes de un vector con su magnitud y dirección) acabo de cubrir, y volveré a más adelante en este capítulo, y nuevamente en el Capítulo 8; las propiedades algebraicas (cómo sumar vectores y multiplicarlos por números ordinarios, que son llamados escalares en este contexto) Voy a introducir en el camino.

Para los primeros capítulos de este semestre, vamos a estar principalmente preocupados por el movimiento en una dimensión (es decir, a lo largo de una línea recta, hacia atrás o hacia adelante), en cuyo caso todo lo que necesitamos para ubicar un punto es un número, su\(x\) (o\(y\), o\(z\)) coordenada; entonces no necesitamos preocuparse particularmente por el álgebra vectorial. Alternativamente, podemos decir simplemente que un vector en una dimensión es esencialmente el mismo que su único componente, que es solo un número positivo o negativo (siendo la magnitud del número la magnitud del vector, y su signo que indica su dirección), y tiene las propiedades algebraicas que siguen naturalmente de eso.

La descripción del movimiento que pretendemos es encontrar una función del tiempo, que denotamos por\(x(t)\), que nos dé la posición del punto (es decir, el valor de\(x\)) para cualquier valor del parámetro de tiempo,\(t\). (Ver Ecuación (\ ref {eq:10}), a continuación, para un ejemplo.) Recuerda que\(x\) representa un número que puede ser positivo o negativo (dependiendo del lado del origen en el que esté el punto), y tiene dimensiones de longitud, por lo que al darle un valor numérico para ello siempre debes incluir las unidades apropiadas (metros, centímetros, millas...). De igual manera,\(t\) representa el tiempo transcurrido desde algún “origen del tiempo” más o menos arbitrario, o tiempo cero. Normalmente siempre\(t\) debe ser positivo, pero en casos especiales puede tener sentido considerar tiempos negativos (piense en cómo contamos los años: “AD” correspondería a “positivo” y “BC” correspondería a negativo, ¡la diferencia es que en realidad no hay año cero!). De todas formas,\(t\) también es un número con dimensiones, y se debe reportar con sus unidades apropiadas: segundos, minutos, horas, etc.

Figura\(\PageIndex{2}\): Un posible gráfico de posición vs. tiempo para un objeto que se mueve en una dimensión

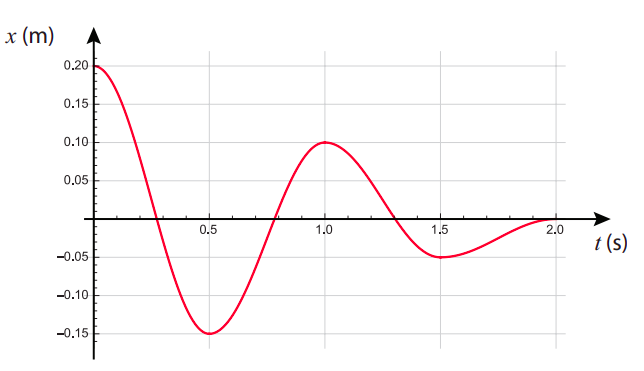
A menudo nos interesará trazar la posición de un objeto en función del tiempo, es decir, la gráfica de la función\(x(t)\). Esto puede, en principio, tener cualquier forma, como se puede ver en la Figura\(\PageIndex{2}\) anterior. En el laboratorio, tendrás la oportunidad de usar un sensor de posición que generará automáticamente gráficos como ese para ti en la computadora, para cualquier objeto en movimiento al que apuntes el sensor de posición. Por lo tanto, es importante que aprendas a “leer” tales gráficas. Por ejemplo, la Figura\(\PageIndex{2}\) muestra un objeto que inicia, en el tiempo\(t\) = 0, una distancia 0.2 m de distancia y a la derecha del origen (así\(x(0)\) = 0.2 m), luego se mueve en la dirección negativa a\(x\) = −0.15 m, que alcanza en\(t\) = 0.5 s; luego gira hacia atrás y se mueve en sentido contrario dirección hasta que alcanza el punto\(x\) = 0.1 m, vuelve a girar, y así sucesivamente. Físicamente, esto podría ser rastrear las oscilaciones amortiguadas de un sistema como un objeto unido a un resorte y deslizarse sobre una superficie que ejerce una fuerza de fricción sobre él (ver Ejemplo 11.5.1).

Desplazamiento

En una dimensión, el desplazamiento de un objeto durante un intervalo de tiempo dado es una cantidad que denotamos como\(\Delta x\), e iguala la diferencia entre las posiciones inicial y final del objeto (en una dimensión, a menudo llamaremos a la “coordenada de posición” simplemente la “posición”, para abreviar):

\[ \Delta x=x_{f}-x_{i} \label{eq:1} \]

Aquí el subíndice\(i\) denota la posición del objeto al inicio del intervalo de tiempo considerado, y el subíndice\(f\) su posición al final del intervalo. El símbolo se\(\Delta\) utilizará consistentemente a lo largo de este libro para denotar un cambio en la cantidad que sigue al símbolo, es decir, la diferencia entre su valor inicial y su valor final. El intervalo de tiempo en sí se escribirá como ∆t y se puede expresar como

\[ \Delta t=t_{f}-t_{i} \]

donde de nuevo\(t_i\) y\(t_f\) son los valores iniciales y finales del parámetro de tiempo (imagina, por ejemplo, que estás leyendo el tiempo en segundos en un reloj digital, y te interesa el cambio en la posición del objeto entre el segundo 130 y el segundo 132: entonces\(t_i\) = 130 s,\(t_2\) = 132 s, y\(\Delta t\) = 2 s).

Se puede practicar la lectura de los desplazamientos de la Figura\(\PageIndex{2}\). El desplazamiento entre\(t_i\) = 0.5 s y\(t_f\) = 1 s, por ejemplo, es 0.25 m (\(x_i\)= −0.15 m,\(x_f\) = 0.1 m). Por otro lado, entre\(t_i\) = 1 s y\(t_f\) = 1.3 s, el desplazamiento es\(\Delta x\) = 0 − 0.1 = −0.1 m

Observe dos cosas importantes sobre el desplazamiento. Primero, puede ser positivo o negativo. Positivo significa que el objeto se movió, en general, en la dirección positiva; negativo significa que se movió, en general, en la dirección negativa. En segundo lugar, incluso cuando es positivo, el desplazamiento no siempre es igual a la distancia recorrida por el objeto (la distancia, por supuesto, siempre se define como una cantidad positiva), porque si el objeto “dobla hacia atrás” en sus pistas por alguna distancia, esa distancia no cuenta para el desplazamiento general. Por ejemplo, mirando nuevamente a la Figura\(\PageIndex{2}\), entre los tiempos\(t_i\) = 0.5 s y\(t_f\) = 1.5 s el objeto se movió primero 0.25 m en la dirección positiva, y luego 0.15 m en la dirección negativa, para una distancia total recorrida de 0.4 m; sin embargo, el desplazamiento total fue de apenas 0.1 m.

A pesar de estas peculiaridades, el desplazamiento total es, matemáticamente, una cantidad útil, porque muchas veces tendremos una manera (es decir, una ecuación) de calcular\(\Delta x\) para un intervalo dado, y luego podremos reescribir la Ecuación (\ ref {eq:1}) para que se lea

\[ x_{f}=x_{i}+\Delta x .\]

Es decir, si sabemos dónde empezó el objeto, y tenemos una forma de calcular\(\Delta x\), podemos averiguar fácilmente dónde terminó. Verás ejemplos de este tipo de cálculo en la tarea más adelante.

Extensión a Dos Dimensiones

En dos dimensiones, escribimos el desplazamiento como el vector

\[ \Delta \vec{r}=\vec{r}_{f}-\vec{r}_{i} .\]

Los componentes de este vector son solo las diferencias en las coordenadas de posición de los dos puntos involucrados; es decir,\( (\Delta \vec r)_x \) (un subíndice\(x\),\(y\), etc., es una forma estándar de representar el componente\(x\),\(y\).. de un vector) es igual a\(x_f - x_i\), y de manera similar \((\Delta \vec{r})_{y}=y_{f}-y_{i}\).

Figura\(\PageIndex{3}\): El vector de desplazamiento para una partícula que inicialmente estaba en un punto con vector de posición\(\vec r_i\) y terminó en un punto con vector de posición\(\vec r_f\) es la diferencia de los vectores de posición.

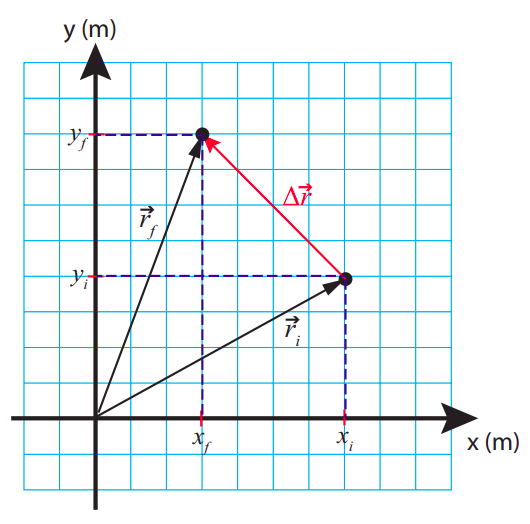
La figura\(\PageIndex{3}\) muestra cómo esto tiene sentido. El\(x\) componente de\(\Delta \vec r\) en la figura es\(\Delta x\) = 3 − 7 = −4 m; el\(y\) componente es\(\Delta y\) = 8 − 4 = 4 m. Esto básicamente te muestra cómo restar (y, por extensión, sumar, ya\( \vec{r}_{f}=\vec{r}_{i}+\Delta \vec{r}\)) vectores: simplemente restas (o sumas) los componentes correspondientes. Observe cómo, según el teorema de Pitágoras, la longitud (o magnitud) del vector de desplazamiento\( |\Delta \vec{r}| = \sqrt{\left(x_{f}-x_{i}\right)^{2}+\left(y_{f}-y_{i}\right)^{2}} \),, es igual a la distancia en línea recta entre el punto inicial y el punto final, al igual que en una dimensión; por supuesto, la partícula podría haber seguido un camino muy diferente desde el inicial hasta el punto final, y por lo tanto recorrió una distancia diferente.

Velocity

Velocidad Media

Si conduces desde Fayetteville a Fort Smith en 50 minutos, tu velocidad promedio para el viaje se calcula dividiendo la distancia de 59.2 mi por el intervalo de tiempo:

\[ \text { average speed }=\frac{\text { distance }}{\Delta t}=\frac{59.2 \: \mathrm{mi}}{50 \: \mathrm{min}}=\frac{59.2 \: \mathrm{mi}}{50 \: \mathrm{min}} \times \frac{60 \: \mathrm{min}}{1 \: \mathrm{hr}}=71.0 \: \mathrm{mph} \label{eq:5} \]

(esta ecuación, por cierto, también te muestra cómo convertir unidades, y cómo se espera que trabajes con cifras significativas este semestre: la regla general es, mantener cuatro cifras significativas en todos los cálculos intermedios y reportar tres en el resultado final).

La forma en que definimos la velocidad promedio es similar a la velocidad promedio, pero con una diferencia importante: usamos el desplazamiento, en lugar de la distancia. Entonces, la velocidad promedio\(v_{av}\) de un objeto, moviéndose a lo largo de una línea recta, a lo largo de un intervalo de tiempo\(\Delta t\) es

\[ v_{a v}=\frac{\Delta x}{\Delta t} \label{eq:6} .\]

Esta definición tiene todas las ventajas y peculiaridades del propio desplazamiento. Por un lado, automáticamente viene con una señal (la misma señal que el desplazamiento, ya que siempre\(\Delta t\) será positiva), que nos dice en qué dirección hemos estado viajando. Por otro lado, puede que no sea una estimación precisa de nuestra velocidad promedio, si duplicamos en absoluto. En el caso más extremo, para un viaje de ida y vuelta (salir de Fayetteville y regresar a Fayetteville), la velocidad promedio sería cero, ya que\(x_f = x_i\) y por lo tanto\(\Delta x\) = 0.

Es claro que este concepto no va a ser muy útil en general, si el objeto que estamos rastreando tiene la posibilidad de doblarse hacia atrás en el intervalo de tiempo\(\Delta t\). Una forma de evitar que esto suceda, y también obtener una estimación más significativa de la velocidad del objeto en cualquier instante, es hacer que el intervalo de tiempo sea muy pequeño. Esto lleva a un nuevo concepto, el de la velocidad instantánea.

Velocidad instantánea

Definimos la velocidad instantánea de un objeto (una “partícula”), en su momento\(t = t_i\), como el límite matemático

\[ v=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t} \label{eq:7} .\]

El significado de esto es el siguiente. Supongamos que calculamos la relación en intervalos de\(\Delta x/\Delta t\) tiempo sucesivamente más pequeños\(\Delta t\) (todos ellos comenzando al mismo tiempo\(t_i\)). Por ejemplo, podemos comenzar por hacer\(t_f = t_i + 1\: s\), luego intentar\(t_f = t_i + 0.5 \: s\), luego\(t_f = t_i + 0.1 \: s\), y así sucesivamente. Naturalmente, a medida que el intervalo de tiempo se vuelve más pequeño, el desplazamiento correspondiente también se volverá más pequeño: la partícula tiene cada vez menos tiempo para alejarse de su posición inicial,\(x_i\). La esperanza es que los ratios\(\Delta x/\Delta t\) sucesivos converjan a un valor definido: es decir, que en algún momento empezaremos a obtener valores muy similares, y que más allá de cierto punto haciendo\(\Delta t\) cualquier menor no cambie ninguno de los dígitos significativos del resultado que nos importa acerca de. Este valor límite es la velocidad instantánea del objeto en ese momento\(t_i\).

Cuando se piensa en ello, hay algo casi un poco contradictorio en el concepto de velocidad instantánea. No se puede (en la práctica) determinar la velocidad de un objeto si todo lo que se le da es un instante literal. Ni siquiera puedes decir si el objeto se está moviendo, ¡si todo lo que tienes es un instante! El movimiento requiere más de un instante, el paso del tiempo. De hecho, todas las velocidades “instantáneas” que podemos medir, con cualquier instrumento, son siempre velocidades realmente medias, solo la media se toma en intervalos de tiempo muy cortos. Sin embargo, el hecho es que para cualquier función de posición razonablemente bien comportada\(x(t)\), el límite en la ecuación (\ ref {eq:7}) está matemáticamente bien definido, y es igual a lo que llamamos, en cálculo, la derivada de la función\(x(t)\):

\[ v=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t} \label{eq:8} .\]

Figura\(\PageIndex{4}\): La pendiente del segmento verde es la velocidad promedio para el intervalo de tiempo\(\Delta t\) mostrado. A medida que\(\Delta t\) se vuelve más pequeño, esto se acerca a la pendiente de la tangente en el punto\((t_i, x_i)\)

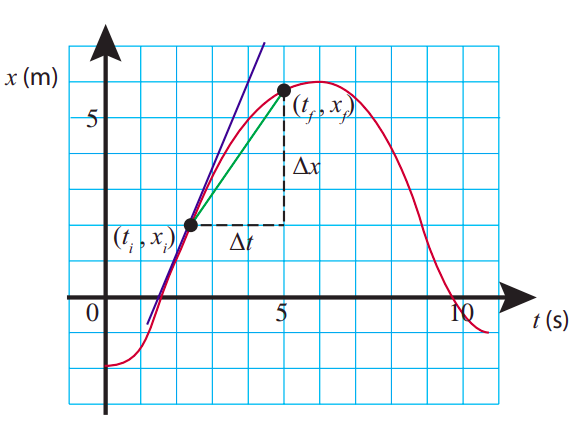
De hecho, hay una interpretación geométrica agradable para esta cantidad: es decir, es la pendiente de una línea tangente a la\(t\) curva\(x\) -vs- en el punto,\((t_i, x_i)\). Como\(\PageIndex{4}\) muestra la Figura, la velocidad promedio\(\Delta x/\Delta t\) es la pendiente (subida sobre carrera) de un segmento de línea dibujado desde el punto\((t_i, x_i)\) hasta el punto\((t_f, x_f)\) (la línea verde en la figura). A medida que hacemos el intervalo de tiempo más pequeño,\(t_f\) acercándonos a\(t_i\) (y por lo tanto, también,\(x_f\) más cerca de\(x_i\)), la pendiente de este segmento se acercará a la pendiente de la línea tangente en\((t_i, x_i)\) (la línea azul), y esta será, por definición (\ ref {eq:7}), la instantánea velocidad en ese punto.

Esta interpretación geométrica facilita la obtención de una sensación cualitativa, a partir del gráfico posición-vs-tiempo, para cuando la partícula se mueve más o menos rápido. Una gran pendiente significa una subida o caída pronunciada, y es entonces cuando la velocidad será mayor, en magnitud. Una subida pronunciada significa una gran velocidad positiva, mientras que una caída pronunciada significa una gran velocidad negativa, por lo que me refiero a una velocidad que viene dada por un número negativo que es grande en valor absoluto. En el futuro, para simplificar oraciones como esta, solo usaré la palabra “velocidad” para referirme a la magnitud (es decir, el valor absoluto) de la velocidad instantánea. Así, la velocidad (como la distancia) es siempre un número positivo, por definición, mientras que la velocidad puede ser positiva o negativa; y una pendiente pronunciada (positiva o negativa) significa que la velocidad es grande allí.

Por el contrario, mirando las\(t\) gráficas de muestra\(x\) -vs- de este capítulo, puede notar que hay momentos en que la tangente es horizontal, es decir, tiene pendiente cero, y así la velocidad instantánea en esos momentos es cero (por ejemplo, en el tiempo\(t\) = 1.0 s en la Figura\(\PageIndex{2}\)). Esto tiene sentido cuando piensas en lo que realmente está haciendo la partícula en esos momentos especiales: simplemente está cambiando de dirección, por lo que su velocidad va, por ejemplo, de positiva a negativa. La forma en que esto sucede es, se ralentiza, baja... la velocidad se hace cada vez más pequeña, y luego, por un instante (literalmente, un punto matemático en el tiempo), se vuelve cero antes, al siguiente instante, va negativo.

Volveremos a esta “lectura de gráficas” en el laboratorio y la tarea, así como en el siguiente capítulo, cuando introduzcamos el concepto de aceleración.

Movimiento con velocidad constante

Si la velocidad instantánea de un objeto nunca cambia, significa que siempre se mueve en la misma dirección con la misma velocidad. En ese caso, la velocidad instantánea y la velocidad promedio coinciden, y eso significa que podemos escribir\(v = \Delta x/ \Delta t\) (donde el tamaño del intervalo ahora\(\Delta t\) podría ser cualquier cosa), y reescribir esta ecuación en la forma

\[ \Delta x = v \Delta t \label{eq:9} \]

que es lo mismo que

\[ x_{f}-x_{i}=v\left(t_{f}-t_{i}\right) \nonumber \]

Ahora supongamos que nos mantenemos\(t_i\) constantes (es decir, fijamos el instante inicial) pero permitimos que el tiempo\(t_f\) cambie, así que solo escribiremos\(t\) para un valor arbitrario de\(t_f\), y\(x\) para el valor correspondiente de\(x_f\). Terminamos con la ecuación

\[ x-x_{i}=v\left(t-t_{i}\right) \nonumber \]

que también podemos escribir como

\[ x(t)=x_{i}+v\left(t-t_{i}\right) \label{eq:10}\]

después de algunos reordenamientos, y donde se\(x(t)\) ha introducido la notación para enfatizar que queremos pensar\(x\) como una función de\(t\). Esta es, no es sorprendente, la ecuación de una línea recta, una “curva” que es su propia tangente y siempre tiene la misma pendiente.

(Por favor, asegúrese de que no está confundido por la notación en la ecuación (\ ref {eq:10}). Los paréntesis alrededor del\(t\) lado izquierdo significan que estamos considerando la posición\(x\) como una función de\(t\). Por otro lado, los paréntesis alrededor de la cantidad\(t − t_i\) en el lado derecho significan que estamos multiplicando esta cantidad por\(v\), lo que aquí es una constante. Esta distinción será particularmente importante cuando introduzcamos la función a\(v(t)\) continuación.)

Cualquiera de las ecuaciones (\ ref {eq:9}) o (\ ref {eq:11}) puede ser utilizada para resolver problemas que involucran movimiento con velocidad constante, y nuevamente verás ejemplos de esto en la tarea.

Movimiento con cambio de velocidad

Si la velocidad cambia con el tiempo, obtener una expresión para la posición del objeto en función del tiempo puede ser una tarea no trivial. En el siguiente capítulo estudiaremos un caso especial importante, a saber, cuando la velocidad cambia a un ritmo constante (aceleración constante).

Para el caso más general, un método gráfico que a veces resulta útil es el siguiente. Supongamos que conocemos la función\(v(t)\), y la graficamos, como en la Figura\(\PageIndex{5}\) a continuación. Entonces el área bajo la curva entre dos instantes cualesquiera, digamos\(t_i\) y\(t_f\), es igual al desplazamiento total del objeto a lo largo de ese intervalo de tiempo.

La idea involucrada se conoce en el cálculo como integración, y va de la siguiente manera. Supongamos que rompo

Figura\(\PageIndex{5}\): Cómo obtener el desplazamiento del área bajo la\(t\) curva\(v\) -vs-.

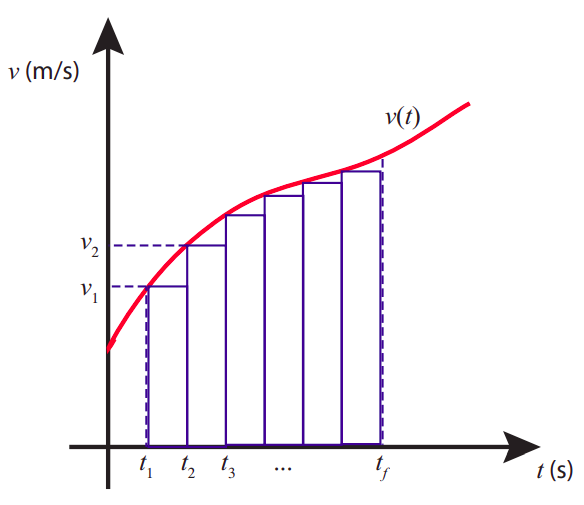
bajando el intervalo de\(t_i\) a\(t_f\) en subintervalos igualmente espaciados, comenzando por el tiempo\(t_i\) (que yo soy, equivalentemente, voy a llamar\(t_1\), es decir,\(t_{1} \equiv t_{i}\), así que tengo ahora\(t_1\),\(t_2\),\(t_3\),... \(t_f\)). Ahora supongamos que trato el movimiento del objeto sobre cada subintervalo como si se tratara de un movimiento a velocidad constante, siendo la velocidad esa al inicio del subintervalo. Esto, por supuesto, es solo una aproximación, ya que la velocidad cambia constantemente; pero, si miras Figura\(\PageIndex{5}\), puedes convencerte de que se convertirá en una aproximación cada vez mejor a medida que aumente el número de puntos intermedios y los rectángulos mostrados en la figura se vuelvan más estrechos y más estrecho. En esta aproximación, el desplazamiento durante el primer subintervalo sería

\[ \Delta x_{1}=v_{1}\left(t_{2}-t_{1}\right) \label{eq:11} \]

donde\(v_1 = v(t_1)\); de manera similar\(\Delta x_2 = v_2(t_3 − t_2)\),, y así sucesivamente.

Sin embargo, la Ecuación (\ ref {eq:11}) es solo el área del primer rectángulo que se muestra bajo la curva en la Figura\(\PageIndex{5}\) (la base del rectángulo tiene “longitud”\(t_2 − t_1\), y su altura es\(v_1\)). De manera similar para el segundo rectángulo, y así sucesivamente. Entonces la suma\(\Delta x_1+\Delta x_2+...\) es tanto una aproximación al área bajo la\(t\) curva\(v\) -vs-, como una aproximación al desplazamiento total\(\Delta t\). A medida que la subdivisión se vuelve cada vez más fina, y los rectángulos cada vez más estrechos (y más numerosos), ambas aproximaciones se vuelven cada vez más precisas. En el límite de “infinitamente muchos”, rectángulos infinitamente estrechos, se obtiene exactamente tanto el desplazamiento total como el área bajo la curva, y ambos son iguales entre sí. Matemáticamente, escribiríamos

\[ \Delta x=\int_{t_{i}}^{t_{f}} v(t) d t \label{eq:12} \]

donde la “S” estilizada (para “suma”) en el lado derecho es el símbolo de la operación conocida como integración en cálculo. Esto es esencialmente lo inverso del proceso conocido como diferenciación, por el cual obtuvimos la función de velocidad de la función de posición, de vuelta en Ecuación (\ ref {eq:8}).

Este método gráfico para obtener el desplazamiento de la función de velocidad a veces es útil, si se puede estimar el área bajo la\(t\) gráfica\(v\) -vs- de manera confiable. Un punto importante a tener en cuenta es que los rectángulos bajo el eje horizontal (correspondientes a velocidades negativas) tienen que agregarse como teniendo área negativa (ya que el desplazamiento correspondiente es negativo); ver ejemplo 1.5.1 al final de este capítulo.

Extensión a Dos Dimensiones

En dos (o más) dimensiones, se define el vector de velocidad promedio como un vector\(\vec v_{av}\) cuyos componentes son\(v_{av,x} = \Delta x/ \Delta t\),\(v_{av,y} = \Delta y/ \Delta t\), y así sucesivamente (donde\(\Delta x\),\(\Delta y\),... son los componentes correspondientes del vector de desplazamiento\(\Delta \vec r \)). Esto se puede escribir de manera equivalente como la ecuación de un solo vector

\[ \vec{v}_{a v}=\frac{\Delta \vec{r}}{\Delta t} \label{eq:13} .\]

Esto te dice cómo multiplicar (o dividir) un vector por un número ordinario: simplemente multiplicas (o divides) cada componente por ese número. Tenga en cuenta que, si el número en cuestión es positivo, esta operación no cambia en absoluto la dirección del vector, simplemente lo escala hacia arriba o hacia abajo (razón por la cual los números ordinarios, en este contexto, se llaman escalares). Si el escalar es negativo, la dirección del vector se voltea como resultado de la multiplicación. Dado que\(\Delta t\) en la definición de velocidad siempre es positiva, se deduce que el vector de velocidad promedio siempre apunta en la misma dirección que el desplazamiento, lo cual tiene sentido.

Para obtener la velocidad instantánea, solo tomas el límite de la expresión (\ ref {eq:13}) como\(\Delta t \rightarrow 0\), para cada componente por separado. El vector resultante\(\vec v\) tiene componentes\(v_x = \lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t} \), etc., que también se pueden escribir como\(v_x = dx/dt, v_y = dy/dt\),...

Todos los resultados obtenidos anteriormente se mantienen para cada dimensión espacial y su componente de velocidad correspondiente. Por ejemplo, el método gráfico que se muestra en la Figura siempre se\(\PageIndex{5}\) puede utilizar para obtener\(\Delta x\) si\(v_x(t)\) se conoce la función, o equivalentemente para obtener\(\Delta y\) si se sabe\(v_y(t)\), y así sucesivamente.

Introducir el vector de velocidad en este punto causa un poco de dificultad notacional. Para cantidades como\(x\) y\(\Delta x\), es bastante obvio que son los\(x\) componentes de los vectores\(\vec r\) y\(\Delta \vec r\) respectivamente; sin embargo, la cantidad que hasta ahora hemos estado llamando simplemente\(v\) debería denotarse más adecuadamente como\(v_x\) (o\(v_y\) si el el movimiento es a lo largo del\(y\) eje). De hecho, existe una convención de que si usas el símbolo para un vector sin la flecha en la parte superior o alguna\(x\)\(y\),,... subíndices, debes significar la magnitud del vector. En este libro, sin embargo, he decidido no seguir esa convención, al menos no hasta que lleguemos al Capítulo 8 (e incluso entonces la utilizaré sólo para las fuerzas). Esto se debe a que pasaremos la mayor parte de nuestro tiempo tratando con el movimiento en una sola dimensión, y hace que la notación sea innecesariamente engorrosa seguir teniendo que escribir los\(y\) subíndices\(x\) o en cada componente de cada vector, cuando realmente solo tienes una dimensión de la que preocuparte en la primera lugar. Entonces, a lo largo de todo, se\(v\) referirá al componente relevante del vector de velocidad, para inferirse del contexto, hasta que lleguemos al Capítulo 8 y en realidad necesitamos tratar tanto con a como a\(v_y\) explícitamente.\(v_x\)

Finalmente, observe que la magnitud del vector de velocidad,\(|\vec{v}|=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}\), es igual a la velocidad instantánea, ya que, como\(\Delta t \rightarrow 0\), la magnitud del vector de desplazamiento,\(|\Delta vec r |\), se convierte en la distancia real recorrida por el objeto en el intervalo de tiempo\(\Delta t\).