1.3: Cambios en el Marco de Referencia y Movimiento Relativo

Todo hasta este punto supone que estamos utilizando un marco de referencia fijo, previamente acordado. Básicamente, esto es solo un origen y un conjunto de ejes a lo largo de los cuales medir nuestras coordenadas, como se muestra en la Figura 1.2.1.

Hay, sin embargo, una serie de situaciones en la física que requieren el uso de diferentes marcos de referencia, y, lo que es más importante, que nos requieren convertir varias cantidades físicas de un marco de referencia a otro. Por ejemplo, imagina que estás en un bote en un río, remando río abajo. Te estás moviendo con cierta velocidad en relación con el agua que te rodea, pero el agua misma fluye con una velocidad diferente en relación con la costa, y tu velocidad real relativa a la orilla es la suma de esas dos cantidades. Los barcos generalmente tienen que hacer este tipo de cálculo todo el tiempo, al igual que los aviones: la “velocidad del aire” es la velocidad de un avión en relación con el aire que lo rodea, pero ese aire suele moverse a una velocidad sustancial en relación con la tierra.

La forma en que tratamos todas estas situaciones es mediante la introducción de dos marcos de referencia, que aquí voy a llamar A y B. Uno de ellos, digamos A, está “en reposo” relativo a la tierra, y el otro está “en reposo” relativo a otra cosa, lo que significa, en realidad, moverse junto con esa otra cosa. (Por ejemplo, un marco de referencia en reposo “relativo al río” sería un marco que se mueve junto con el agua del río, como un trozo de madera flotante con la que podrías medir tu progreso en relación con.)

En cualquier caso, gráficamente, esto se verá como en la Figura\(\PageIndex{1}\), que he dibujado para el caso bidimensional porque creo que hace más fácil visualizar lo que está pasando:

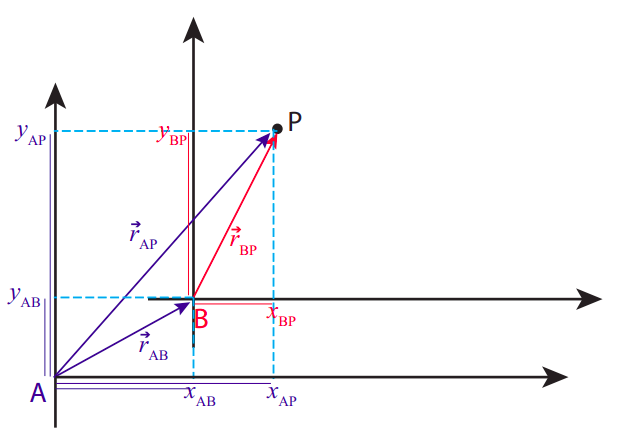
Figura\(\PageIndex{1}\): Vectores de posición y coordenadas de un punto P en dos marcos de referencia diferentes, A y B.

En el marco de referencia A, el punto P tiene coordenadas de posición\((x_{AP} , y_{AP})\). De igual manera, en el marco de referencia B, sus coordenadas son\((x_{BP} , y_{BP})\). Como puede ver, la notación elegida es tal que cada coordenada en A tendrá una “A” como primer subíndice, mientras que el segundo subíndice indica el objeto al que se refiere, y de manera similar para las coordenadas en B.

Las coordenadas\((x_{AB}, y_{AB})\) son especiales: son las coordenadas, en el marco de referencia A, del origen del marco de referencia B. Esto es suficiente para ubicar completamente el marco B en A, siempre y cuando los fotogramas no se roten uno con relación al otro.

Las finas líneas coloreadas que he dibujado a lo largo de los ejes de la Figura\(\PageIndex{1}\) están destinadas a dejar claro que las siguientes ecuaciones sostienen:

\ [\ begin {array} {l}
{x_ {A P} =x_ {A B} +x_ {B P}}\\
{x_ {A P} =x_ {A B} +x_ {B P}}
\ end {array}\ label {eq:14}\]

Si bien la figura está dibujada para el caso fácil donde todas estas cantidades son positivas, deberías poder convencerte de que las Eqs. (\ ref {eq:14}) mantener también cuando una o más de las coordenadas tienen valores negativos.

Todas estas coordenadas son también los componentes de los respectivos vectores de posición, mostrados en la figura y codificados por colores por marco de referencia (así, por ejemplo,\ (\ vec r_ {AP}\) es el vector de posición de P en el fotograma A), por lo que las ecuaciones (\ ref {eq:14}) pueden escribirse de manera más compacta como la única ecuación vectorial

\ [\ vec r_ {AP} =\ vec r_ {AB} +\ vec r_ {BP}\ etiqueta {eq:15}.\]

De todo esto puedes ver cómo agregar vectores: algebraicamente, solo agregas sus componentes por separado, como en Eqs. (\ ref {eq:14}); gráficamente, los dibujas para que la punta de un vector coincida con la cola del otro (a esto lo llamamos “punta a cola”), y luego dibujas el vector suma desde la cola del primero hasta la punta del otro. (En general, para obtener dos vectores arbitrarios punta a cola puede que necesites desplazar uno de ellos; esto está bien siempre que no cambies su orientación, es decir, siempre que solo lo desplaces, no lo rotes. Veremos cómo funciona esto en un momento con velocidades, y más adelante con fuerzas.)

Por supuesto, ya te mostré cómo restar vectores con la Figura 1.2.3: nuevamente, algebraicamente, solo restas las coordenadas correspondientes, mientras que gráficamente las dibujas con un origen común, y luego dibujas el vector de la punta del vector que estás restando a la punta del otro. Si vuelve a leer el párrafo anterior, puede ver que la Figura 1.2.3 puede ser igualmente utilizada para mostrar que\ (\ Delta\ vec r = \ vec r_f -\ vec r_f -\ vec r_i\), como para mostrar que\ (\ vec r_f =\ vec r_i +\ Delta\ vec r\).

De manera similar, se puede ver gráficamente a partir de la Figura\(\PageIndex{1}\) (o algebraicamente de la Ecuación (\ ref {eq:15}) que el vector de posición de P en el fotograma B viene dado por\(\vec r_{BP} = \vec r_{AP} − \vec r_{AB}\). El último término en esta expresión se puede escribir de una manera diferente, de la siguiente manera. Si sigo la convención que he introducido anteriormente, la cantidad \(x_{BA}\) (con el orden de los subíndices invertidos) sería la \(x\) coordenada del origen del fotograma A en el fotograma B, y algebraicamente eso sería igual a\(−x_{AB}\), y de manera similar \(y_{BA} = −y_{AB}\). De ahí que se mantenga la igualdad vectorial\ (\ vec r_ {AB} = −\ vec r_ {BA}\). Entonces,

\ [\ vec {r} _ {B P} =\ vec {r} _ {A P} -\ vec {r} _ {A B} =\ vec {r} _ {A P} +\ vec {r} _ {B A}\ etiqueta {eq:16}.\]

Esto es, en cierto modo, el “inverso” de la Ecuación (\ ref {eq:15}): nos dice cómo obtener la posición de P en el fotograma B si conocemos su posición en el fotograma A.

Déjame mostrarte a continuación cómo todo esto se extiende a los desplazamientos y velocidades. Supongamos que el punto P indica la posición de una partícula en ese momento\(t\). A lo largo de un intervalo de tiempo\(\Delta t\), tanto la posición de la partícula como la posición relativa de los dos marcos de referencia pueden cambiar. Podemos agregar otro subíndice,\(i\) o\(f\), (para inicial y final) a las coordenadas, y escribir, por ejemplo,

\ [\ begin {array} {l}
{x_ {A P, i} =x_ {A B, i} +x_ {B P, i}}\\
{x_ {A P, f} =x_ {A B, f} +x_ {B P, f}}
\ end {array}\ etiqueta {eq:17}\]

Restar estas ecuaciones nos da los desplazamientos correspondientes:

\ [\ Delta x_ {A P} =\ Delta x_ {A B} +\ Delta x_ {B P}\ etiqueta {eq:18}.\]

Dividiendo la ecuación (\ ref {eq:18}) por\ (\ Delta t\) obtenemos las velocidades promedio\(^1\), y luego tomando el límite \(\Delta t \rightarrow 0\) obtenemos las velocidades instantáneas. Esto se aplica de la misma manera a las\(y\) coordenadas, y el resultado es la ecuación vectorial

\ [\ vec {v} _ {A P} =\ vec {v} _ {B P} +\ vec {v} _ {A B}\ etiqueta {eq:19}.\]

He reorganizado los términos en el lado derecho para (ojalá) facilitar la visualización de lo que está pasando. En palabras: la velocidad de la partícula P relativa a (o medida en) el fotograma A es igual a la suma (vector) de la velocidad de la partícula medida en el cuadro B, más la velocidad del fotograma B en relación con el cuadro A.

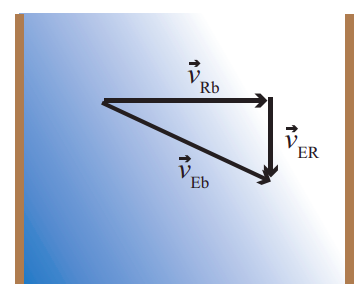
El resultado (\ ref {eq:19}) es justo lo que hubiéramos esperado de los ejemplos que mencioné al inicio de esta sección, como remar en un río o un avión volando al viento. Por ejemplo, para el avión\(\vec v_{BP}\) podría ser su “velocidad aerodinámica” (solo tiene que ser un vector, por lo que sería más como su “velocidad del aire”: es decir, su velocidad relativa al aire que lo rodea), y\(\vec v_{AB}\) sería la velocidad del aire relativa a la tierra (la velocidad del viento, a la ubicación del avión). En otras palabras, A representa el marco de referencia terrestre y B el marco de referencia de aire, o viento. Entonces,\ (\ vec v_ {AP}\) sería la velocidad “verdadera” del avión con relación a la tierra. Se puede ver cómo sería importante sumar estas cantidades como vectores, en general, considerando lo que sucede cuando vuelas en un viento cruzado, o intentas remar a través de un río, como en la Figura \(\PageIndex{2}\) a continuación.

Figura\(\PageIndex{2}\): Remar a través de un río. Si te dirijas “recto a través” del río (con vector de velocidad\(\vec v_{Rb}\) en el marco móvil del río, que fluye con velocidad\(\vec v_{ER}\) en el marco de la tierra), tu velocidad real relativa a la costa será el vector\(\vec v_{Eb}\). Esta es una instancia de la Ecuación (\ ref {eq:19}), con el marco A siendo E (la tierra), el marco B siendo R (el río), y “b” (para “barco”) de pie para el punto P que estamos rastreando.

Como puedes ver en este par de ejemplos, la Ecuación (\ ref {eq:19}) suele ser útil tal como está escrita, pero a veces la información que tenemos se nos da de una manera diferente: por ejemplo, se nos podría dar la velocidad del objeto en el fotograma A\((\vec v_{AP})\), y la velocidad del fotograma B como se ve en el cuadro A\((\vec v_{AB})\), y se le dijo que calculara la velocidad del objeto como se ve en el cuadro B. Esto se puede lograr fácilmente si observamos que el vector\(\vec v_{AB}\) es igual a\(-\vec v_{BA}\); es decir, la velocidad del fotograma B como se ve desde el fotograma A es justo lo contrario de la velocidad del fotograma A como se ve desde el cuadro B. Por lo tanto, la ecuación (\ ref {eq:19}) se puede reescribir como

\ [\ vec {v} _ {A P} =\ vec {v} _ {B P} -\ vec {v} _ {B A}\ etiqueta {eq:20}.\]

Para la mayoría de los próximos capítulos vamos a estar considerando solo el movimiento en una dimensión, y así escribiremos la Ecuación (\ ref {eq:19}) (o (\ ref {eq:20})) sin los símbolos vectoriales, y se entenderá que\(v\) se refiere al componente del vector a\(\vec v\) lo largo del eje de coordenadas de interés.

Una cantidad que será particularmente importante más adelante es la velocidad relativa de dos objetos, que podríamos etiquetar 1 y 2. La velocidad del objeto 2 en relación con el objeto 1 es, por definición, la velocidad que un observador que se mueve junto con 1 mediría para el objeto 2. Entonces es solo un simple cambio de marco: dejar que el marco de tierra sea el marco E y el marco que se mueve con el objeto 1 sea el fotograma 1, entonces la velocidad que queremos es \(v_{12}\) (“velocidad del objeto 2 en el fotograma 1"). Si hacemos el cambio\(\rightarrow\) A1, B\(\rightarrow\) E, y P \(\rightarrow\) 2 en la Ecuación (\ ref {eq:20}), obtenemos

\ [v_ {12} =v_ {E 2} -v_ {E 1}\ etiqueta {eq:21} .\]

En otras palabras, la velocidad de 2 con relación a 1 es solo la velocidad de 2 menos la velocidad de 1. Esto vuelve a ser un efecto familiar: si estás conduciendo por la carretera a 50 millas por hora, y el auto frente a ti circula a 55, entonces su velocidad relativa a ti es de 5 mph, que es la velocidad a la que se aleja de ti (en la dirección hacia adelante, se supone que es la positiva) .

Es importante darse cuenta de que todas estas velocidades son velocidades reales, cada una en su propio marco de referencia. Se puede decir que algo se mueve realmente a cierta velocidad en un marco de referencia, y igual de que realmente se mueve con una velocidad diferente en un marco de referencia diferente. Tendré mucho más que decir sobre esto en el próximo capítulo, pero mientras tanto puedes reflexionar sobre el hecho de que, si un auto que se mueve a 55 mph choca con otro que se mueve a 50 mph en la misma dirección, el daño será básicamente el mismo que si el primer auto se hubiera estado moviendo a 5 mph y el segundo había estado en reposo. Para fines prácticos, en lo que a usted respecta, la velocidad de otro automóvil relativa a la suya es la velocidad “real” de ese automóvil.

Recursos

Una buena app para practicar cómo agregar vectores (y cómo dividirlos en componentes, magnitud y dirección, etc.) se puede encontrar aquí: https://phet.colorado.edu/en/simulation/vector-addition.

Quizás la demostración más dramática de cómo funciona Equation (\ ref {eq:19}) en el mundo real es en este episodio de Mythbusters: https://www.youtube.com/watch?v=BLuI118nhzc. (Si este enlace no funciona, haz una búsqueda de “Los Cazadores de Mitos cancelan el impulso”). Disparan una pelota desde la cama de un camión, con una velocidad (relativa a la camioneta) de 60 mph hacia atrás, mientras que el camión avanza a 60 mph. Creo que vale la pena ver el resultado. (No se distraiga con su charla sobre el impulso. Llegaremos ahí, a tiempo.)

Un video muy antiguo, pero también muy bueno, educativo sobre diferentes marcos de referencia es este: https://www.youtube.com/watch?v=sS17fCom0Ns. Deberías tratar de ver al menos parte de ella. Muchas cosas serán relevantes para partes posteriores del curso, incluido el movimiento de proyectiles, y toda la discusión sobre el movimiento relativo que viene a continuación, en el Capítulo 2.

---

\(^1\)Hemos hecho una suposición muy natural, que el intervalo de tiempo\(\Delta t\) es el mismo para los observadores que rastrean el movimiento de la partícula en los fotogramas A y B, respectivamente (donde se entiende que cada observador se mueve junto con su fotograma). Esto, sin embargo, resulta no ser cierto cuando alguna de las velocidades involucradas está cerca de la velocidad de la luz, y así la simple fórmula de adición de velocidades (\ ref {eq:19}) no se sostiene en la teoría de la relatividad de Einstein. (Esta es en realidad la primera parte de física real de la que te he hablado en este libro, hasta ahora; desafortunadamente, ¡no vas a tener ningún uso para ello este semestre!)