1.5: Ejemplos

Ejemplo\(\PageIndex{1}\): Movimiento con velocidad constante (por tramos)

Te vas de casa en tu bicicleta para ir a visitar a un amigo. A tu velocidad normal de 9 mph, sabes que te lleva 6 minutos llegar allí. Esta vez, sin embargo, cuando has recorrido la mitad de la distancia te das cuenta de que olvidaste un libro en casa que ibas a regresar con tu amigo, así que te das la vuelta y pedaleas al doble de tu velocidad normal, vuelves a casa, agarra el libro y vuelves a empezar por la casa de tu amigo a 18 mph (imagínate ¡están realmente en forma de lograr esto!)

1. ¿Qué tan lejos de ti vive tu amigo?
2. ¿Cuál es la distancia total que recorres en este viaje?
3. ¿Cuánto tardó todo el viaje?
4. Dibuja una posición versus tiempo y una gráfica de velocidad versus tiempo para todo el viaje. Utilice unidades SI para ambas gráficas. Olvida el tiempo que te lleva detenerte y darte la vuelta, y también el tiempo que te lleva correr hacia tu casa y agarrar el libro (en otras palabras, asume que esos cambios en tu dirección de movimiento ocurren instantáneamente).
5. Demuestre explícitamente, usando su\(t\) gráfica\(v\) -vs-, que el método gráfico de la Figura 1.2.5 le da el desplazamiento total para su viaje.

Solución

Voy a resolver este problema usando tanto millas como unidades SI, la primera porque parece más natural, y la segunda porque se nos pide usar unidades SI para la parte (d), así que bien podríamos usarlas desde el principio. En general, debes usar unidades SI siempre que puedas. Si no estás seguro de qué hacer en un problema específico, ¡pregúntale a tu instructor!

(a) Nos dicen que a 9 millas por hora tardarían 6 minutos en llegar, así que vamos a usar

\ [\ Delta x = v\ Delta t \ etiqueta {eq:22}\]

con\(v\) = 9 mph y\(\Delta t\) = 6 min. Tenemos que convertir las horas en minutos, o viceversa. Nuevamente, en este caso parece más fácil darse cuenta de que 6 min equivale a 1/10 de hora, entonces:

\ [\ Delta x=\ izquierda (9\ frac {\ texto {millas}} {\ texto {hr}}\ derecha)\ veces 0.1\:\ mathrm {hr} =0.9 \:\ text {millas.}\ label {eq:23}\]

En unidades SI, 9 mph = 4.023 m/s, y 6 min = 360 s, así\(\Delta x\) = 1448 m.

b) Esto es sólo una cuestión de hacer un seguimiento de la distancia recorrida en las distintas partes del viaje. Empiezas montando la mitad de la distancia hasta la casa de tu amigo, es decir, 0.45 millas, y luego vuelves a montarlo de nuevo a casa, así que eso es 0.9 millas, y luego estás de vuelta donde empezaste, así que aún tienes que ir los 0.9 kilómetros hasta la casa de tu amigo. Entonces, en general, recorres 1.8 millas, o 2897 m.

(c) Todo el viaje consta, como se detalló anteriormente, de 0.45 millas a 9 mph, y el resto, que es de 1.35 millas, a 18 mph. Aplicando\(\Delta t = \Delta x/v\) a cada uno de estos intervalos, obtenemos un tiempo total de

\ begin {align}
\ Delta t &=\ frac {0.45\:\ text {millas}} {9\: \ mathrm {mph}} +\ frac {1.35\:\ text {millas}} {18\: \ mathrm {mph}} =0.125\:\ text {horas}\ nonumber\\
&=0.125\ times 60\:\ mathrm {min} =7.5\:\ mathrm {min}\ nonumber \\
&=7.5\ veces 60\:\ mathrm {s} =450\:\ mathrm {s} \ label {eq:24}
\ end {align}

d) A continuación se muestran las gráficas. A continuación se detallan cómo conseguirlos.

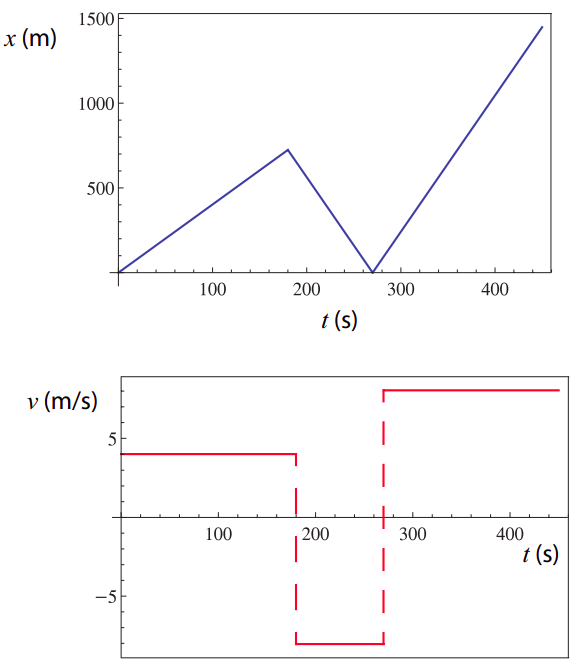
• Primer intervalo: de\(t\) = 0 a\(t\) = 180 s (3 min, que es lo que se necesitaría para cubrir la mitad de la distancia a la casa de tu amigo a 9 mph). La velocidad es una constante\(v\) = 4.023 m/s Para la gráfica de posición, use la Ecuación (1.2.10) con\(x_i\) = 0,\(t_i\) = 0 y\(v\) = 4.023 m/s.
• Segundo intervalo: de\(t\) = 180 s a\(t\) = 270 s ( te lleva la mitad de 3 min, es decir 90 s, para cubrir la misma distancia que la anterior al doble de velocidad). La velocidad es una constante\(v\) = −8.046 m/s (el doble de lo que era antes, pero en sentido contrario). Para la gráfica de posición, usa la Ecuación (1.2.10) con\(x_i\) = 724 m (esto es la mitad de la distancia a la casa de tu amigo, y la posición inicial para este intervalo),\(t_i\) = 180 s y \(v\) = −8.046 m/s.
• Tercer intervalo: de\(t\) = 270 s a\(t\) = 450 s. la velocidad es una constante\(v\) = 8.046 m/s (misma velocidad que justo antes, pero en sentido contrario). Para la gráfica de posición, usa la Ecuación (1.2.10) con\(x_i\) = 0 m (comienzas de nuevo en tu casa), \(t_i\) = 270 s y\(v\) = 8.046 m/s.

Si está familiarizado con el paquete de software Mathematica, el gráfico de posición se produjo usando el comando

Parcela [Si [t<180, 4.023 t, Si [t<270, 4.023*180-8.046 (t-180), 8.046 (t-270)]], {t, 0, 450}]

y el gráfico de velocidad se produjo usando

Parcela [Si [t<180, 4.023, Si [t<270, -8.046, 8.046]], {t, 0, 450}]

(y luego conectar las líneas horizontales a mano, lo cual no es necesario, sino que ayuda a visualizar lo que está pasando).

Las gráficas también podrían haberse producido utilizando el paquete de software de trazado gratuito Gnuplot (disponible aquí: http://www.gnuplot.info/download.html) con los siguientes comandos:

gnuplot> set ficticio t
gnuplot> f (t) = t<180? 4.023*t: t<270? 4.023*180-8.046* (t-180): 8.046* (t-270)
gnuplot> parcela [0:450] f (t)

La primera línea establece la variable independiente predeterminada en\(t\) (en lugar de\(x\), que es lo que Gnuplot espera). La segunda línea define la función por tramos usando el operador ternario (? :) prestado del lenguaje de programación C. La tercera línea traza la función sobre el rango indicado.

(e) Para ello necesitamos encontrar el área bajo la\(t\) gráfica\(v\) -vs- que acabamos de trazar. Básicamente, tenemos tres rectángulos: el primero tiene base 180 unidades (s) y altura 4 unidades (m/s), por lo que su área es de 4\(\times\) 180 = 720 (m). El segundo rectángulo tiene base 90 unidades y altura −8 (negativo, ¡porque está por debajo del eje horizontal!) , por lo que su área es −720. El último tiene base 180 unidades nuevamente (de 270 a 450) y altura 8, por lo que su área es de 8 \(\times\) 180 = 1440. Entonces el área total “debajo” de la\(t\) curva\(v\) -vs- es

\[ 720 - 72 +1440 = 1440 \: \text{meters} \nonumber \]

que es (aproximadamente) tu desplazamiento total, es decir, las 9 millas a la casa de tu amigo. (Por supuesto, habríamos obtenido un resultado más preciso si hubiéramos usado los valores más precisos para las “alturas” de 4.023, −8.046 y 8.046, pero si todo lo que tenemos que pasar es la gráfica, tal precisión es prácticamente imposible).

Ejemplo\(\PageIndex{2}\): Adición de velocidades, movimiento relativo

Este ejemplo se inspiró en la demostración de “carrera en una acera en movimiento” en http://physics.bu.edu/~duffy/classroom.html. ¡Por favor ve a echarle un vistazo!

Dos chicas, Ann y Becky (sí, A y B) deciden tener una carrera mientras esperan un avión en un aeropuerto casi desierto. Ann correrá por la pasarela móvil, hasta el final de la misma (que está a 30 m de distancia) y hacia atrás, mientras que Becky correrá a su lado en el piso (no móvil), también a 30 m de ida y vuelta. La pasarela se mueve a 1 m/s, y las niñas corren a la misma velocidad constante de 5 m/s con relación a la superficie en la que están paradas.

1. En relación con el piso (no móvil), ¿cuál es la velocidad de Ann para el primer tramo de su carrera, cuando se mueve en la misma dirección que la pasarela (tomar esa para ser la dirección positiva)? ¿Cuál es su velocidad para la pierna de retorno?
2. ¿Cuánto tiempo tarda cada una de las chicas en completar su carrera?
3. Cuando ambas chicas corren en la dirección positiva, ¿cuál es la velocidad de Becky con respecto a Ann? (Es decir, ¿qué tan rápido ve Ann a Becky moverse y en qué dirección?)
4. Cuando Ann se da la vuelta y comienza a correr en dirección negativa, pero Becky sigue corriendo en la dirección positiva, ¿cuál es la velocidad de Becky en relación con Ann?
5. ¿Cuál es la distancia total que recorre Ann en el marco de referencia de la pasarela móvil?

Solución

Voy a resolver esto en el formato que se te requerirá usar este semestre para la mayoría de los problemas de tareas y exámenes. No voy a poder hacer esto por cada ejemplo, ¡pero deberías! Por favor, siga esto cuidadosamente.

Para empezar, debes dibujar un boceto de la situación descrita en el problema, lo suficientemente detallado como para incluir toda la información relevante que te den. Aquí está el mío:

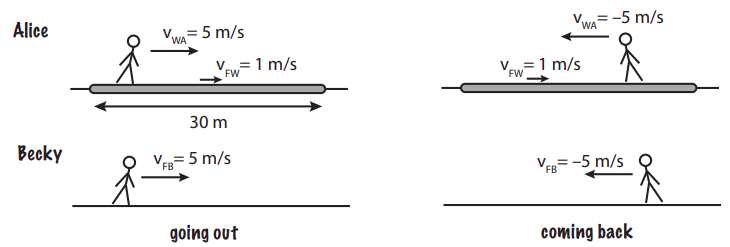
Tenga en cuenta que he dibujado un cuadro por cada mitad de la carrera, y que toda la información que se da en el texto del problema está ahí. La figura deja en claro también la notación que estaré usando para cada una de las velocidades de las chicas, y para ver de un vistazo lo que está sucediendo.

A continuación debes indicar qué tipo de problema es este y qué resultado básico (teorema, principio o ecuación (s)) vas a utilizar para resolverlo. Para este problema, se podría decir:

“Este es un problema relativo de transformación de movimiento/marco de referencia. Voy a usar la Ecuación (1.3.6)

\ [\ vec {v} _ {A P} =\ vec {v} _ {B P} +\ vec {v} _ _ {A B}\ nonumber \]

así como la ecuación básica para el movimiento con velocidad constante:”

\[ \Delta x = v \Delta t \nonumber .\]

Después de eso, resuelve cada parte por turno, ¡y asegúrate de mostrar todo tu trabajo!

(a) Deje que F se coloque para el marco de referencia del piso y W el marco de la pasarela. En la notación de la Sección 1.3, tenemos\(v_{FW}\) = 1 m/s. Para el partido de ida de su carrera, se nos dice que la velocidad de Ann con respecto a la pasarela es de 5 m/s, así\(v_{W A}\) = 5 m/s. Luego, por la Ecuación (1.3.6) (con el siguiente cambio de índices: A\(\rightarrow\) F, B \(\rightarrow\)W y P\(\rightarrow\) A),

\ [v_ {F A} =v_ {F W} +v_ {W A} =1 \ frac {\ mathrm {m}} {\ mathrm {s}} +5\ frac {\ mathrm {m}} {\ mathrm {s}} =6 \ frac {\ mathrm {m}} {\ mathrm {s}}\ etiqueta {eq:25}\]

(cuando ves una ecuación como esta, llena de subíndices, es una buena práctica leerla, mentalmente, para ti mismo: “La velocidad de Ann en relación con el piso es igual a la velocidad de la pasarela en relación con el piso más la velocidad de Ann en relación con la pasarela”. ¡Entonces tómate un momento para ver si tiene sentido! Aquí hay un lugar donde la imagen puede ser de gran ayuda.)

Para el tramo de retorno, use la misma fórmula, pero tenga en cuenta que ahora su velocidad relativa a la pasarela es negativa,\(v_{W A}\) = −5 m/s, ya que se mueve en sentido contrario:

\ [v_ {F A} =v_ {F W} +v_ {W A} =1 \ frac {\ mathrm {m}} {\ mathrm {s}} -5\ frac {\ mathrm {m}} {\ mathrm {s}} =-4 \ frac {\ mathrm {m}} {\ mathrm {s}}\ etiqueta {eq:26}.

(b) En relación con el marco de referencia del piso, acabamos de ver que Ann primero cubre 30 m a una velocidad de 6 m/s, y luego los mismos 30 m a una velocidad de 4 m/s, por lo que su tiempo total es

\ [\ Delta t_ {A} =\ frac {30\:\ mathrm {m}} {6\:\ mathrm {m}/ \ mathrm {s}} +\ frac {30\:\ mathrm {m}} {4\ mathrm {m}/\ mathrm {s}} =5\: \ mathrm {s} +7.5\:\ mathrm {s} =12.5\:\ mathrm {s}\ label {eq:27} \]

mientras que Becky solo corre 30 m a 5 m/s en ambos sentidos, así que le toma 6 s de cualquier manera, para un total de 12 s, lo que significa que gana la carrera.

(c) La cantidad que queremos está escrita, en la notación de la Sección 1.3,\(v_{AB}\) (“velocidad de Becky relativa a Ann”). Para calcular esto, solo necesitamos conocer las velocidades de ambas chicas en algún marco de referencia (¡lo mismo para ambas!) , luego resta la velocidad de Ann de la de Becky (esto es lo que dice la Ecuación (1.3.8)). En este caso, si solo elegimos el marco de referencia del piso, tenemos\(v_{F A}\) = 6 m/s y\(v_{F B}\) = 5 m/s, entonces

\ [v_ {A B} =v_ {F B} -v_ {F A} =5 \ frac {\ mathrm {m}} {\ mathrm {s}} -6\ frac {\ mathrm {m}} {\ mathrm {s}} =-1 \ frac {\ mathrm {m}} {\ mathrm {s}}\ label {eq:28}\

El signo negativo tiene sentido: Ann ve a Becky cayendo detrás de ella, así que en relación con ella Becky se mueve hacia atrás, es decir, en la dirección que hemos identificado como negativa.

(d) Nuevamente usamos la misma ecuación, y la velocidad de Becky sigue siendo la misma, pero ahora la velocidad de Ann es\(v_{F A}\) = −4 m/s (¡nota el signo negativo!) , entonces

\ [v_ {A B} =v_ {F B} -v_ {F A} =5 \ frac {\ mathrm {m}} {\ mathrm {s}} -\ left (-4 \ frac {\ mathrm {m}} {\ mathrm {s}}\ right) =9 \ frac {\ mathrm {m}} {\ mathrm {s}\ etiqueta eq:29}\]

(e) Esto puede resultarle un poco sorprendente, pero si lo piensa la explicación de por qué Ann perdió la carrera, a pesar de que corrió a la misma velocidad que Becky en relación con la superficie en la que estaba parada, tiene que ser que en realidad corrió una distancia más larga en esa superficie! Ya que estaba corriendo por un total de 12.5 s a una velocidad constante (¡no velocidad!) de 5 m/s en el marco de la pasarela, luego en ese marco corrió una distancia\ (d = |v| \ Delta t = 5\ times 12.5 = 62.5\) m Esa es la longitud total de la pasarela que realmente pisó.