3.3: Sistemas Extendidos y Centro de Masa

Considerar una colección de partículas con masas\(m_1\),\(m_2\),..., y localizadas, en algún instante dado, en posiciones\(x_1\),\(x_2\)... (Todavía estamos, por el momento, considerando solo el movimiento en una dimensión, pero todos estos resultados se generalizan fácilmente a tres dimensiones.) El centro de masa de dicho sistema es un punto matemático cuya coordenada de posición viene dada por

\[ x_{c m}=\frac{m_{1} x_{1}+m_{2} x_{2}+\ldots}{m_{1}+m_{2}+\ldots} \label{eq:3.8} .\]

Claramente, el denominador de (\ ref {eq:3.8}) es solo la masa total del sistema, que podemos simplemente denotar por\(M\). Si todas las partículas tienen la misma masa, el centro de masa estará de alguna manera “en el medio” de todas ellas; de lo contrario, tenderá a estar más cerca de las partículas más masivas. Las “partículas” en cuestión podrían separarse, o podrían ser literalmente las “partes” en las que elegimos subdividir, con fines computacionales, un solo objeto extendido.

Si las partículas están en movimiento, la posición del centro de masa,\(x_{cm}\), en general cambiará con el tiempo. Para un objeto sólido, donde todas las partes se mueven juntas, el desplazamiento del centro de masa simplemente será el mismo que el desplazamiento de cualquier parte del objeto. En el caso más general, tendremos (restando\(x_{cmi}\) de\(x_{cmf}\))

\[ \Delta x_{c m}=\frac{1}{M}\left(m_{1} \Delta x_{1}+m_{2} \Delta x_{2}+\ldots\right) \label{eq:3.9} .\]

Dividiendo la ecuación (\ ref {eq:3.9}) por\(\Delta t\) y tomando el límite como\(\Delta t \rightarrow 0\), obtenemos la velocidad instantánea del centro de masa:

\[ v_{c m}=\frac{1}{M}\left(m_{1} v_{1}+m_{2} v_{2}+\ldots\right) \label{eq:3.10} .\]

Pero esto es solo

\[ v_{c m}=\frac{p_{s y s}}{M} \label{eq:3.11} .\]

donde\(p_{sys} = m_1v_1 + m_2v_2 + \ldots\) está el impulso total del sistema.

Movimiento del Centro de Masa para un Sistema Aislado

La ecuación (\ ref {eq:3.11}) es un resultado muy interesante. Dado que el impulso total de un sistema aislado es constante, nos dice que el centro de masa de un sistema aislado de partículas se mueve a velocidad constante, independientemente del movimiento relativo de las propias partículas o de sus posibles interacciones entre sí. Como se indicó anteriormente, esto generaliza de manera directa a más de una dimensión, por lo que podemos escribir\(\vec v_{cm} = \vec p_{sys}/M\). Así, podemos decir que, para un sistema aislado en el espacio, no sólo la velocidad, sino también la dirección de movimiento de su centro de masa no cambia con el tiempo.

Claramente este resultado es una especie de generalización de la ley de la inercia. Para un objeto sólido y extendido, de hecho, nos proporciona la forma precisa que debe tomar la ley de inercia: en ausencia de fuerzas externas, el centro de masa simplemente se moverá en línea recta con velocidad constante, mientras que el objeto mismo puede estar moviéndose de cualquier manera que no afecte la trayectoria del centro de masa. Específicamente, el movimiento más general de un cuerpo rígido aislado es un movimiento en línea recta de su centro de masa a velocidad constante, combinado con una posible rotación del objeto en su conjunto alrededor del centro de masa.

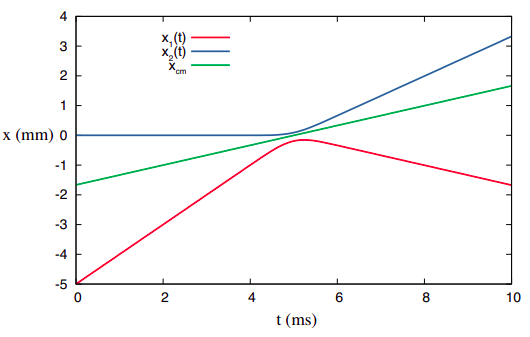
Para un sistema que consiste en partes separadas, por otro lado, el centro de masa es generalmente solo un punto en el espacio, que puede o no coincidir en cualquier momento con la posición de cualquiera de las partes, pero que no obstante se moverá a velocidad constante siempre y cuando el sistema esté aislado. Esto se ilustra en la Figura\(\PageIndex{1}\), donde se han dibujado las curvas de posición vs. tiempo para los objetos colisionantes de la Figura 3.1.1. He asumido que el objeto 1 comienza en\(x_{1i}\) = −5 mm en\(t\) = 0, y el objeto 2 comienza en\(x_{2i}\) = 0 en\(t\) = 0. Debido a que el objeto 2 tiene el doble de inercia del objeto 1, la posición del centro de masa, dada por la Ecuación (\ ref {eq:3.8}), siempre será

\[ x_{c m}=x_{1} / 3+2 x_{2} / 3 \nonumber \]

es decir, el centro de masa siempre estará entre los objetos 1 y 2, y su distancia del objeto 2 siempre será la mitad de su distancia al objeto 1:

\ [\ begin {alineado}
&\ izquierda|x_ {c m} -x_ {1}\ derecha|=\ frac {2} {3}\ izquierda|x_ {1} -x_ {2}\ derecha|\\
&\ izquierda|x_ {c m} -x_ {2}\ derecha|=\ frac {1} {3}\ izquierda|x_ {1} -x_ {2}\ derecha|
\ fin {alineado}\]

La figura\(\PageIndex{1}\) muestra que esta simple prescripción sí da como resultado un movimiento con velocidad constante para el centro de masa (la línea recta verde), a pesar de que\(t\) las curvas\(x\) -vs- de los dos objetos en sí parecen relativamente complicadas. (¡Por favor compruébalo! Lleva una regla a Figura\(\PageIndex{1}\) y verifica que el centro de masa esté, a cada instante, donde se supone que debe estar.)

Figura 3.1.1. La línea verde muestra la posición del centro de masa en función del tiempo.

El concepto de centro de masa nos da una forma importante de simplificar la descripción del movimiento de sistemas potencialmente complicados. Haremos un buen uso de ella en próximos capítulos.

Una muy agradable demostración del movimiento del centro de masa en colisiones bicorporales unidimensionales se puede encontrar en https://phet.colorado.edu/sims/collision-lab/collision-lab_en.html (es necesario marcar la casilla “centro de masa” para verla).

Recoil y Propulsión de Cohetes

Como acabamos de ver, no se puede alterar el movimiento de su centro de masa sin depender de alguna fuerza externa, es decir, algún tipo de soporte externo. Esto es en realidad algo que quizás hayas experimentado cuando estás descansando sobre una superficie muy resbaladiza y simplemente no puedes “agarrarla”. Hay, sin embargo, una manera de sortear este problema que, de hecho, se basa en la conservación del impulso mismo: si llevas algo contigo, y puedes tirarlo lejos de ti a gran velocidad, retrocederás como resultado de eso. Si puedes seguir lanzando cosas, tú (con tu tienda de cosas aún sin tirar) acelerarás un poco más cada vez. Este es, en esencia, el principio detrás de la propulsión de cohetes.

Matemáticamente, considera dos objetos, de masas\(m_1\) y\(m_2\), inicialmente en reposo, por lo que su impulso total es cero. Si la masa 1 se tira de la masa 2 con una velocidad\(v_{1f}\), entonces, por conservación del impulso (siempre asumiendo que el sistema está aislado) debemos tener

\[ 0=m_{1} v_{1 f}+m_{2} v_{2 f} \label{eq:3.12} \]

y por lo tanto\(v_{2f} = −m_1v_{1f}/m_2\). Es así como un cohete se mueve hacia adelante, expulsando constantemente la masa (el gas de escape caliente) hacia atrás a una alta velocidad. Obsérvese que, aunque ambos objetos se muevan, el centro de masa de todo el sistema no lo hace (en ausencia de cualquier fuerza externa), como se discutió anteriormente.