3.5: Ejemplos

Última actualización
Guardar como PDF

Page ID: 128277

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ejemplo\(\PageIndex{1}\): Lectura de un gráfico de colisión

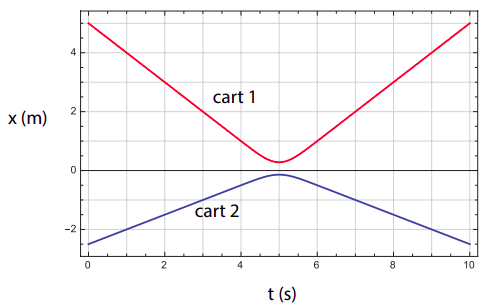
El gráfico muestra una colisión entre dos carros (posiblemente equipados con imanes para que se repelan entre sí antes de que realmente se toquen) en una pista aérea. La inercia (masa) del carro 1 es de 1 kg. Nota: ¡este es un gráfico de posición vs. tiempo!

¿Cuáles son las velocidades iniciales de los carros?
¿Cuáles son las velocidades finales de los carros?
¿Cuál es la masa del segundo carro?
¿La pista aérea parece estar nivelada? ¿Por qué? (Pista: ¿la gráfica muestra alguna evidencia de aceleración, para cualquiera de los carros, fuera de la región de colisión?)
En el momento de la colisión, ¿la aceleración del primer carro es positiva o negativa? ¿Qué tal el segundo carro? (Justifica tus respuestas.)
Para el sistema que consta de los dos carros, ¿cuál es su impulso inicial (total)? ¿Cuál es su impulso final?
Imagina ahora que uno de los imanes está invertido, así que cuando los carros chocan se pegan entre sí. ¿Cuál sería entonces el impulso final del sistema? ¿Cuál sería su velocidad final?

Figura\(\PageIndex{1}\): Una colisión entre dos carros

Solución

(a) Todas las velocidades deben calcularse escogiendo una parte recta fácil de cada curva y calculando

\ [v=\ frac {\ Delta x} {\ Delta t} \ nonumber\]

para intervalos adecuados. De esta manera uno consigue

\ begin {alineado}
&v_ {1 i} =-1\:\ frac {\ mathrm {m}} {\ mathrm {s}}\\
&v_ {2 i} =0.5\:\ frac {\ mathrm {m}} {\ mathrm {s}}
\ end {alineado}

b) Del mismo modo, se obtiene

\ begin {alineado}
&v_ {1 f} =1\:\ frac {\ mathrm {m}} {\ mathrm {s}}\\
&v_ {2 f} =-0.5\:\ frac {\ mathrm {m}} {\ mathrm {s}}
\ end {alineado}

\ begin {alineado}
&\ frac {m_ {2}} {m_ {1}} =-\ frac {\ Delta v_ {1}} {\ Delta v_ {2}}\\
&\ frac {m_ {2}} {m_ {1}} =-\ frac {1- (-1)} {-0.5-0.5} =2
\ end {alineado}

por lo que la masa del segundo carro es de 2 kg.

(d) Sí, la pista parece estar nivelada porque los carros no muestran ninguna evidencia de aceleración fuera de la región de colisión (las curvas de posición vs. tiempo son líneas rectas fuera de la región aproximadamente dadas por 4.5 s <\(t\) < 5.5 s).

e) La aceleración del primer carro es positiva. Se puede ver esto ya sea gráficamente (la curva es como una parábola que se abre hacia arriba, es decir, cóncava), o algebraicamente (la velocidad del carro aumenta, pasando de −1 m/s a 1 m/s)

De igual manera, la aceleración del segundo carro es negativa. La curva es como una parábola que se abre hacia abajo, es decir, convexa; o, algebraicamente, la velocidad del carro disminuye, pasando de 0.5 m/s a −0.5 m/s.

f) El impulso inicial del sistema es

\ [p_ {i} =m_ {1} v_ {1 i} +m_ {2} v_ {2 i} =( 1\:\ mathrm {kg})\ veces\ izquierda (-1\: \ frac {\ mathrm {m}} {\ mathrm {s}}\ derecha) + (2\:\ mathrm {kg}) \ veces\ izquierda (0.5\:\ frac {\ mathrm {m}} {\ mathrm {s}}\ derecha) =0\ nonumber \]

El impulso final es

\ [p_ {f} =m_ {1} v_ {1 f} +m_ {2} v_ {2 f} =( 1\:\ mathrm {kg})\ veces\ left (1\: \ frac {\ mathrm {m}} {\ mathrm {s}}\ derecha) + (2\:\ mathrm {kg}) \ veces\ izquierda (-0.5\:\ frac {\ mathrm {m}} {\ mathrm {s}}\ derecha) =0 \ nonumber\]

También se podría simplemente decir que el impulso final debería ser el mismo que el impulso inicial, ya que el sistema parece estar aislado.

g) El impulso debe conservarse también en este caso, por lo que\(p_f\) = 0. La velocidad sería

\[ v_{f}=\frac{p_{f}}{m_{1}+m_{2}}=0 \nonumber .\]

Ejemplo\(\PageIndex{2}\): Colisión en diferentes marcos de referencia, centro de masa y retroceso

Un jugador de hockey de 80 kg (llámalo jugador 1), moviéndose a 3 m/s hacia la derecha, choca con un jugador de 90 kg (jugador 2) que se movía a 2 m/s a la izquierda. Por un breve momento, están pegados deslizándose juntos mientras se agarran el uno al otro.

¿Cuál es su velocidad conjunta a medida que se deslizan juntas?
¿Cuál era la velocidad de su centro de masa antes y después de la colisión?
¿Cómo le parece la colisión a otro jugador que estaba patinando inicialmente a 1.5 m/s a la derecha? Da todas las velocidades iniciales y finales tal como las ve este jugador, y demuestra explícitamente que el impulso también se conserva en el marco de referencia de este jugador.
Eventualmente, el jugador de 90 kg logra empujar al otro hacia atrás, de tal manera que el jugador 1 (el jugador de 80 kg) termina moviéndose a 1 m/s a la izquierda con relación al jugador 2. ¿Cuáles son sus velocidades finales en el marco de referencia terrestre?

Solución

(a) Llamar a las velocidades iniciales \(v_{1i}\) y\(v_{2i}\), a la velocidad final conjunta\(v_f\), y asumir que los dos jugadores son un sistema aislado para fines prácticos. Entonces la conservación del impulso lee

\ [m_ {1} v_ {1 i} +m_ {2} v_ {2 i} =\ izquierda (m_ {1} +m_ {2}\ derecha) v_ {f}\ etiqueta {eq:3.13}.\]

Resolviendo para la velocidad final, obtenemos

\ [v_ {f} =\ frac {m_ {1} v_ {1 i} +m_ {2} v_ {2 i}} {m_ {1} +m_ {2}}\ etiqueta {eq:3.14}.\]

Sustituyendo los valores dados, obtenemos

\ [v_ {f} =\ frac {80\ times 3-90\ times 2} {170} =0.353\:\ frac {\ mathrm {m}} {\ mathrm {s}}\ label {eq:3.15} .\]

(b) Según la Ecuación (3.3.3), la velocidad del centro de masa,\(v_{cm}\), es exactamente la misma que la que acabamos de calcular (Ecuación\ ref {eq:3.14}) anterior). Esto tiene sentido: después de la colisión, si los jugadores se mueven juntos, el centro de masa de su sistema tiene que estar moviéndose con ellos. Además, si el sistema está aislado, el centro de velocidad másica debe ser el mismo antes y después de la colisión. Entonces la respuesta es\(v_{cm}\) = \(v_f\) = 0.353 m/s.

(c) Permítanme referirme a este tercer jugador como “jugador 3", e introducir un subíndice “3" para referirme a las cantidades como se ve en su marco de referencia. Que también el subíndice “\(E\)” denote el marco de referencia original, “Tierra”. De la Ecuación (1.3.6), tenemos entonces (para el jugador 1, por ejemplo)

\ [v_ {31} =v_ {3 E} +v_ {E 1} =v_ {E 1} -v_ {E 3}\ etiqueta {eq:3.16}\]

porque\(v_{3E}\), la “velocidad de la Tierra en el marco de referencia del jugador 3", es claramente igual a \(−v_{E3}\), la negativa de la velocidad del jugador 3 relativa a la Tierra. Básicamente, lo que dice la Ecuación (\ ref {eq:3.16}) es que para convertir todas las velocidades del fotograma Tierra al marco de referencia del jugador 3, solo necesitamos restarles 1.5 m/s. Esto nos da

\ [\ begin {align}
v_ {31, i} &=3\:\ frac {\ mathrm {m}} {\ mathrm {s}} -1.5\: \ frac {\ mathrm {m}} {\ mathrm {s}} =1.5\:\ frac {\ mathrm {m}} {\ mathrm {s}} \ noner\
v_ {, i} &=-2\:\ frac {\ mathrm {m}} {\ mathrm {s}} -1.5\: \ frac {\ mathrm {m}} {\ mathrm {s}} =-3.5\:\ frac {\ mathrm {m}} {\ mathrm {s}} \ nonumber\\
v_ {31, f} =v_ {32, f} &=0.353\: \ frac {\ mathrm {m}} {\ mathrm {s}} -1.5\: \ frac {\ mathrm {m}} {\ mathrm {s}} =-1.147\: \ frac {\ mathrm {m}} {mathrm {s}}\ label {eq:3.17}
\ end {align}\]

El impulso inicial total en el marco de referencia 3 del jugador es entonces

\ [p_ {s y s, i} =m_ {1} v_ {31, i} +m_ {2} v_ {32, i} =80\ veces 1.5+90\ veces (-3.5) =-195 \ frac {\ mathrm {kg}\ cdot\ mathrm {m}} {\ mathrm {s}}\ etiqueta {eq:3.18} \]

y el impulso final es

\ [p_ {\ text {sys}, f} =\ izquierda (m_ {1} +m_ {2}\ derecha) v_ {31, f} =170\ times (-1.147) =-195\: \ frac {\ mathrm {kg}\ cdot\ mathrm {m}} {\ mathrm {s}}\ label {eq:3.19} .\]

Por lo que el impulso total se conserva en el marco de referencia del jugador 3. La razón de esto es que se trata de un marco de referencia inercial, porque la velocidad del jugador 3 no cambia.

(d) Para esta parte del problema, volvemos al marco de referencia original (el marco de referencia de la Tierra), y podemos dejar caer el subíndice “\(E\)”. Para este nuevo proceso, las velocidades finales de la parte (a) se convierten en las velocidades iniciales, por lo que tenemos\(v_{1i}\)\(v_{2i}\) = = 0.353 m/s. [Nota: alternativamente, dado que el sistema está aislado a lo largo, estaría bien en este caso usar las velocidades antes de la colisión para calcular su impulso total, que también necesita ser conservado en este proceso.] También se nos dice que la velocidad final del jugador 1 respecto al jugador 2 es\(v_{21,f}\) =\ (v_ {1f} − v_ {2f}\) = −1 m/s Así que tenemos dos ecuaciones que resolver:

\ [\ begin {align}
\ left (m_ {1} +m_ {2}\ right)\ times\ left (0.353\: \ frac {\ mathrm {m}} {\ mathrm {s}}\ right) &=m_ {1} v_ {1 f} +m_ {2} v_ {2 f}\ quad\ text {(conservación del impulso)}\ nonumber\\
v_ {1 f} -v_ {2 f} &=-1\:\ frac {\ mathrm {m}} {\ mathrm {s}} \ quad (\ texto {final velocidad relativa})\ label {eq:3.20}
\ end {align}\]

Dejando a un lado las unidades por el momento, para que las ecuaciones sean más legibles (las unidades finales funcionarán, si nos aseguramos de usar unidades SI todo el tiempo), tenemos:

\ [\ begin {align}
(80+90)\ times 0.353 &=80 v_ {1 f} +90 v_ {2 f}\\
v_ {1 f} &=v_ {2 f} -1\ label {eq:3.21}
\ end {align}\]

Ahora sustituya la segunda ecuación, por la que ya he “resuelto”\(v_{1f}\), en la primera ecuación y resuelva para\(v_{2f}\). El resultado es\(v_{2f}\) = 0.824 m/s, que, cuando se sustituye de nuevo en la ecuación de velocidad relativa, da\(v_{1f}\) = −0.176 m/s.