5.7: Temas Avanzados
- Page ID
- 128227
Dos carros colisionando y comprimiendo un resorte
A diferencia del Ejemplo 5.6.2, que consideraba un resorte estacionario y solo planteaba preguntas sobre los estados inicial y final, este ejemplo pretende mostrarte cómo se pueden usar “métodos de energía” para resolver el movimiento real de un sistema relativamente complicado en función del tiempo. El sistema son los dos carros que colisionan, uno de ellos equipado con un resorte, considerados en la Sección 5.1. Aunque toda la física involucrada es directa, las matemáticas están en un nivel superior al que usarás este semestre, así que estoy presentando esto aquí solo como una “curiosidad”.
Primero, recordar que la energía cinética total para un problema de colisión se puede escribir como\(K = K_{cm} + K_{conv}\), donde (si el sistema está aislado)\(K_{cm}\) permanece constante en todo momento. Entonces, la energía mecánica total\(E = K + U = K_{cm} + K_{conv} + U\). Esto también es constante, y antes de que ocurra la interacción, cuando\(U\) = 0\(E = K_{cm} + K_{conv,i}\), tenemos, así que estableciendo estas dos cosas iguales y cancelando\(K_{cm}\) obtenemos
\[ K_{\text {conv}}=K_{\text {conv}, i}-U \label{eq:5.15} \]
donde la función de energía potencial viene dada por la Ecuación (5.1.6). Introduciendo la coordenada relativa\(x_{12} = x_2 − x_1\), y la velocidad relativa\(v_{12}\), la ecuación (\ ref {eq:5.15}) se convierte en
\[ \frac{1}{2} \mu v_{12}^{2}=\frac{1}{2} \mu v_{12, i}^{2}-\frac{1}{2} k\left(x_{12}-x_{0}\right)^{2} \label{eq:5.16} \]
una ecuación que debe mantenerse mientras se desarrolla la interacción. Podemos resolver esto para\(v_{12}\), y luego notar que ambos\(x_{12}\) y\(v_{12}\) son funciones del tiempo, y esta última es la derivada con respecto al tiempo de la primera, entonces
\[ v_{12}=\pm \sqrt{v_{12, i}^{2}-(k / \mu)\left(x_{12}-x_{0}\right)^{2}} \label{eq:5.17} \]
\[ \frac{d x_{12}}{d t}=\pm \sqrt{v_{12, i}^{2}-(k / \mu)\left(x_{12}(t)-x_{0}\right)^{2}} \label{eq:5.18} .\]
(El signo “\(\pm\)” significa que la cantidad del lado derecho tiene que ser negativa al principio, cuando los carros se van juntando, y positiva después, cuando se van deshaciendo. Esto se debe a que he asumido que el carrito 1 comienza a la izquierda del carrito 2, por lo que ir en el carrito 2, como se ve desde el carrito 1, parece estar moviéndose hacia la izquierda.)
La ecuación (\ ref {eq:5.18}) es lo que se conoce, en cálculo, como una ecuación diferencial. El problema es encontrar una función de\(t\),\(x_{12}(t)\), tal que cuando tomas su derivada obtengas la expresión en el lado derecho. Si sabes calcular derivados, puedes comprobar que la solución es de hecho
\[ x_{12}(t)=x_{0}-\frac{v_{12, i}}{\omega} \sin \left[\omega\left(t-t_{c}\right)\right] \quad \text { for } t_{c} \leq t \leq t_{c}+\pi / \omega \label{eq:5.19} \]
donde la cantidad\(\omega = \sqrt{k/ \mu}\), y el tiempo\(t_c\) es el carro de tiempo 1 primero hace contacto con el resorte:\(t_c = (x_{2i} −x_0 −x_{1i})/v_{1i}\). La solución (\ ref {eq:5.19}) es válida mientras el resorte esté comprimido, es decir, por el tiempo que, o\(x_{12}(t) < x_0\)\( \sin \left[\omega\left(t-t_{c}\right)\right]>0 \), lo que se traduce en la condición en que\(t\) se muestra arriba.
Al tener una solución para\(x_{12}\), ahora podríamos obtener resultados explícitos para\(x_1(t)\) y\(x_2(t)\) por separado, utilizando el hecho de que\(x_1 = x_{cm} −m_2x_{12}/(m_1+m_2)\), y\(x_2 = x_{cm} +m_1x_{12}/(m_1 +m_2)\) (comparar Eqs. (4.2.1), en el capítulo 4), y encontrar la posición del centro de masa en función del tiempo es un problema trivial, ya que simplemente se mueve con velocidad constante.
Sin embargo, no necesitamos hacer nada de esto para generar las gráficas de la energía cinética y potencial que se muestran en la Figura 5.1.2: la energía potencial depende únicamente de\(x_2 − x_1\), la cual viene dada explícitamente por la Ecuación (\ ref {eq:5.19}), y la energía cinética es igual a\(K_{cm} + K_{conv}\), donde \(K_{cm}\)es constante y\(K_{conv}\) viene dada por la Ecuación (\ ref {eq:5.16}), que también se puede reescribir fácilmente en términos de Ecuación (\ ref {eq:5.19}). Los resultados son Eqs. (5.1.7) en el texto.
Obtención de la función de energía potencial de los datos de colisión
Considere la colisión ilustrada en la Figura 3.3.1 (de vuelta en el Capítulo 3). ¿Podemos decir cuál es la función de energía potencial para la interacción entre los dos carros?
A primera vista, puede parecer que toda la información necesaria para “reconstruir” la función ya\(U(x_1−x_2)\) está disponible, al menos en forma gráfica: De la Figura 3.3.1 se podría obtener el valor de\(x_2 − x_1\) en cualquier momento\(t\); luego de la Figura 4.2.1 se puede obtener el valor de \(K\)(en el escenario de colisión elástica) para el mismo valor de\(t\); y luego podría trazar\(U = E − K\) (donde\(E\) está la energía total) en función de\(x_2 − x_1\).
Pero hay una trampa: La figura 3.3.1 muestra que los objetos colisionantes nunca se acercan más\(x_2−x_1\) que 0.28 mm, así que no tenemos forma de decir qué\(U(x_2−x_1)\) es para valores más pequeños de\(x_2−x_1\). ¡Este es esencialmente el problema que enfrentan los físicos de partículas cuando usan colisiones (que hacen regularmente) para tratar de determinar la naturaleza precisa de las interacciones entre las partículas que estudian!
Puedes comprobarlo por ti mismo. Las funciones para las que utilicé\(x_1(t)\) y\(x_2(t)\) en la Figura 3.3.1 son
\ begin {align}
&x_ {1} (t) =\ frac {1} {3}\ izquierda ((2 t-10)\ nombreoperador {erf} (10-2 t) +10\ nombreoperador {erf} (10) +t-\ frac {e^ {-4 (t-5) ^ {2}}} {\ sqrt {\ pi}}\ no derecha) -5\ umber\\
&x_ {2} (t) =\ frac {1} {3}\ izquierda ((5-t)\ nombreoperador {erf} (10-2 t) -5\ nombreoperador {erf} (10) +t+\ frac {e^ {-4 (t-5) ^ {2}}} {2\ sqrt {\ pi}}\ derecha)\ label {eq:5.20}
\ end {align}
Aquí, “erf” es la llamada “función de error”, que puedes encontrar en cualquier biblioteca decente de funciones matemáticas. Esto parece complicado, pero solo te da las formas que deseas para las curvas de velocidad. La derivada de lo anterior es
\ begin {align}
&v_ {1} (t) =\ frac {1} {3} (1+2\ operatorname {erf} (10-2 t))\ nonumber\\
&v_ {2} (t) =\ frac {1} {3} (1-\ operatorname {erf} (10-2 t))\ label {eq:5.21} final
\ {alinear}
y es posible que desee intentar trazarlos usted mismo; el resultado debe ser la Figura 3.1.1.
Ahora, supongamos (como hice para la Figura 4.2.1) que\(m_1\) = 1 kg, y\(m_2\) = 2 kg, y use estos valores y los resultados de Eq (\ ref {eq:5.21}) (se supone que está en m/s) para calcular\(K_{sys}\) como una función de\(t\). Luego\(U = E_{sys} − K_{sys}\), con\(E_{sys}\) = 1/2 J:
\[ U=\frac{1}{2}-\frac{1}{2} m_{1} v_{1}^{2}(t)-\frac{1}{2} m_{2} v_{2}^{2}(t)=\frac{1}{3}\left(1-\operatorname{erf}^{2}(10-2 t)\right) \label{eq:5.22} \]
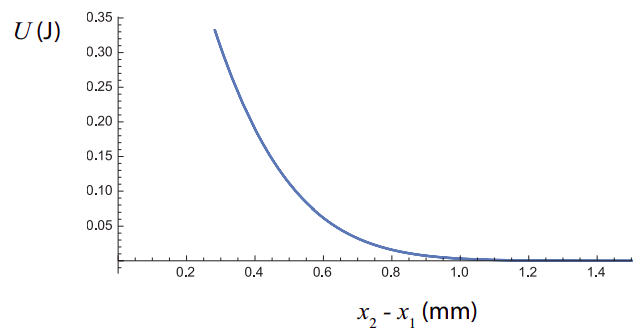
y ahora hacer una gráfica paramétrica de\(U\) versus\(x_2 − x_1\), usando\(t\) como parámetro. Terminarás con una figura como la de abajo: