6.2: Fuerzas y Energía Potencial
- Page ID
- 128135
En el último capítulo mencioné un caso especial que encontramos a menudo, en el que un objeto más ligero está interactuando con uno mucho más masivo, de manera que el masivo esencialmente no se mueve en absoluto como resultado de la interacción. Tenga en cuenta que esto no contradice la tercera ley de Newton, Ecuación (6.1.5): las fuerzas que los dos objetos ejercen entre sí son las mismas en magnitud, pero la aceleración de cada objeto es inversamente proporcional a su masa, así\(F_{12} = −F_{21}\) implica
\[ m_{2} a_{2}=-m_{1} a_{1} \label{eq:6.12} \]
y así si, por ejemplo\(m_{2} \gg m_{1}\),, obtenemos\(\left|a_{2}\right|=\left|a_{1}\right| m_{1} / m_{2} \ll\left|a_{1}\right|\). En palabras, el objeto más masivo responde menos que el menos masivo a una fuerza de la misma magnitud. ¡Así es como se nos ocurrió el concepto de masa inercial en primer lugar!
De todas formas, recordarán que en esta situación podría simplemente escribir la función de energía potencial de todo el sistema como una función únicamente de la coordenada del objeto más ligero,\(U(x)\). Voy a usar esta configuración simplificada para mostrarte una relación muy interesante entre energías y fuerzas potenciales. Supongamos que se trata de un sistema cerrado en el que no se está produciendo disipación de energía. Entonces la energía mecánica total es una constante:
\[ E_{\text {mech}}=\frac{1}{2} m v^{2}+U(x)=\text { constant } \label{eq:6.13} \]
(Aquí,\(m\) está la masa del objeto más ligero, y\(v\) su velocidad; el objeto más masivo no contribuye a la energía cinética total, ¡ya que no se mueve!)
A medida que el objeto más ligero se mueve, ambos\(x\) y\(v\) en la Ecuación (\ ref {eq:6.13}) cambian con el tiempo (recordemos, por ejemplo, nuestro estudio de “paisajes energéticos” en el capítulo anterior, sección 5.1). Entonces puedo tomar la derivada de la Ecuación (\ ref {eq:6.13}) con respecto al tiempo, usando la regla de la cadena, y señalando que, dado que todo es una constante, el valor total de la derivada debe ser cero:
\ begin {align}
0 &=\ frac {d} {d t}\ izquierda (\ frac {1} {2} m (v (t)) ^ {2} +U (x (t))\ derecha)\ nonumber\\
&=m v (t)\ frac {d v} {d t} +\ frac {d U} {d x}\ frac {d x} {d t}\ label {eq:6.14}.
\ end {align}
Pero tenga en cuenta que\(dx/dt\) es lo mismo que\(v(t)\). Así puedo cancelar eso en ambos términos, y luego me quedo con
\[ m \frac{d v}{d t}=-\frac{d U}{d x} \label{eq:6.15} .\]
Pero\(dv/dt\) es solo la aceleración\(a\), y\(F = ma\). Así que esto me dice que
\[ F=-\frac{d U}{d x} \label{eq:6.16} \]
y así es como siempre se puede obtener la fuerza de una función energética potencial.
Vamos a comprobarlo de inmediato por la fuerza de gravedad: lo sabemos\(U^G = mgy\), entonces
\[ F^{G}=-\frac{d U^{G}}{d y}=-\frac{d}{d y}(m g y)=-m g \label{eq:6.17} .\]
¿Es esto correcto? ¡Parece ser! Recordemos que todos los objetos caen con la misma aceleración, −\(g\) (suponiendo que la dirección hacia arriba sea positiva), así que si\(F = ma\), debemos tener\(F^G = −mg\). Entonces la fuerza gravitacional ejercida por la tierra sobre cualquier objeto (que denotaría en su totalidad por\(F^G_{E,o}\)) es proporcional a la masa inercial del objeto —de hecho, es lo que llamamos el peso del objeto— pero ya que para obtener la aceleración hay que dividir la fuerza por la masa inercial, esa cancela, y\(a\) termina siendo lo mismo para todos los objetos, independientemente de lo pesados que sean.
Ahora que tenemos este resultado en nuestro haber, podemos pasar al caso un poco más desafiante de dos objetos de masas comparables que interactúan a través de una función energética potencial que debe ser, como señalé en el capítulo anterior, una función solo de la coordenada relativa\(x_{12} = x_2 − x_1\).
Afirmo que en ese caso se puede volver a obtener la fuerza sobre el objeto 1\(F_{21}\),, tomando la derivada de\(U(x_2 − x_1)\) con respecto a\(x_1\) (dejando\(x_2\) solo), y recíprocamente, se obtiene\(F_{12}\) tomando la derivada de\(U(x_2 − x_1)\) con respecto a\(x_2\). Así es como funciona, nuevamente usando la regla de la cadena:
y se puede ver que esto automáticamente asegura eso\(F_{21} = −F_{12}\). De hecho, fue para asegurar esto que requerí que\(U\) debía depender sólo de la diferencia de\(x_1\) y\(x_2\), más que de cada uno por separado. Ya que obtuvimos la condición\(F_{21} = −F_{12}\) originaria de la conservación del impulso, se puede ver ahora cómo se relacionan las dos cosas 1.
El único ejemplo que hemos visto hasta ahora de este tipo de función energética potencial fue en la Sección 5.1 del capítulo pasado, para dos carros que interactúan a través de un resorte “ideal”. Te dije ahí que la energía potencial del sistema podría escribirse como\(\frac{1}{2} k(x_2 − x_1 − x_0)^2\), donde\(k\) estaba la “constante de primavera” y\(x_0\) la longitud relajada de la primavera. Si aplica Eqs. (\ ref {eq:6.18}) a esta función, encontrarás que la fuerza ejercida (a través del muelle) por el carrito 2 en el carrito 1 es
\[ F_{21}=k\left(x_{2}-x_{1}-x_{0}\right) \label{eq:6.19} .\]
Tenga en cuenta que esta fuerza será negativa bajo los supuestos que hicimos el último capítulo, es decir, que el carro 2 está a la derecha, el carro 1 a la izquierda, y el resorte está comprimido, de manera que\(x_2 − x_1 < x_0\). Del mismo modo,
\[ F_{12}=-k\left(x_{2}-x_{1}-x_{0}\right) \label{eq:6.20} \]
y ésta, como debería, es positiva.
Los resultados (\ ref {eq:6.19}) y (\ ref {eq:6.20}) básicamente te dicen lo que entendemos por un “resorte ideal” en física: es un resorte que tira (si se estira) o empuja (si se comprime) con una fuerza que es proporcional al cambio de su longitud de equilibrio. Por lo tanto, si sujetas un extremo del resorte en\(x\) = 0, y lo estiras o lo comprimes para que el otro extremo esté en\(x\), el resorte responderá ejerciendo una fuerza
\[ F^{s p r}=-k\left(x-x_{0}\right) \label{eq:6.21} .\]
Como puede ver, esto es negativo si\(x > x_0 > 0\) (resorte estirado, fuerza de tracción) y positivo si\(x < x_0\) (resorte comprimido, fuerza de empuje). De hecho, el resorte ejerce una fuerza igual (en magnitud) y opuesta (en dirección) en el otro extremo (la unida a la pared), por lo que la Ecuación (\ ref {eq:6.21}) solo da el signo correcto de la fuerza al final que se denota por el valor de la coordenada\(x\). Las ecuaciones (\ ref {eq:6.19}) y (\ ref {eq:6.20}) son un poco más claras a este respecto: La ecuación (\ ref {eq:6.19}) da el signo correcto de la fuerza en el punto\(x_1\), y la Ecuación (\ ref {eq:6.20}) el signo correcto en el punto\(x_2\).
La figura\(\PageIndex{1}\) muestra, en negro, todas las fuerzas ejercidas por un resorte con un extremo fijo, según sea relajado, comprimido o estirado. He asumido que es empujado o tirado por una mano (no mostrada) en el extremo “libre”, de ahí el subíndice “\(h\)”, mientras que el subíndice “\(w\)” significa “muro”. Obsérvese que la pared y la mano, a su vez, ejercen fuerzas iguales y opuestas sobre el resorte, mostradas en rojo en la figura.
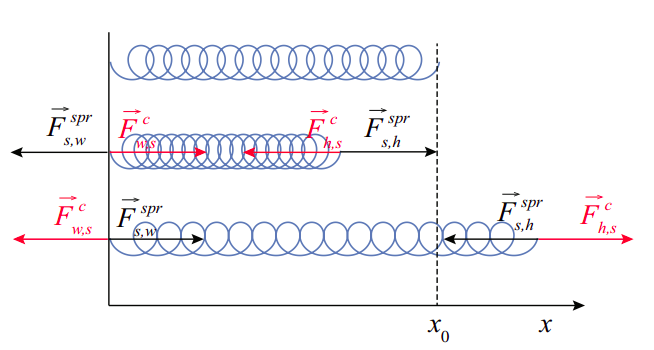
La ecuación (\ ref {eq:6.21}) se conoce generalmente como la ley de Hooke, después del científico británico Robert Hooke (contemporáneo de Newton). Por supuesto, no es una “ley” en absoluto, meramente una aproximación útil a la forma en que se comportan la mayoría de los resortes siempre y cuando no los estires ni los comprimas demasiado 2.
Una nota sobre la forma en que las fuerzas han sido etiquetadas en la Figura\(\PageIndex{1}\). He utilizado el símbolo genérico “\(c\)”, que significa “contacto”, para indicar el tipo de fuerza ejercida por la pared y la mano sobre el resorte. De hecho, dado que cada par de fuerzas (por la mano en el resorte y por el resorte en la mano, por ejemplo), en el punto de contacto, surge de una y la misma interacción, debería haber usado la misma notación de “tipo” para ambos, pero es una práctica generalizada usar un superíndice como “spr” para denotar una fuerza cuya origen es, en última instancia, la elasticidad de un resorte. Esto no cambia el hecho de que la fuerza del resorte, en el punto donde se aplica, es efectivamente una fuerza de contacto.
Entonces, a continuación, una palabra sobre las fuerzas de “contacto”. Básicamente, lo que queremos decir con eso son fuerzas que surgen donde los objetos “tocan”, y lo entendemos por oposición a lo que en cambio se llaman fuerzas de “campo” (como la gravedad, o fuerzas magnéticas o electrostáticas) que “actúan a distancia”. La distinción en realidad solo es significativa a nivel macroscópico, ya que a nivel microscópico los objetos nunca se tocan realmente, y todas las fuerzas son fuerzas de campo, es solo que algunas son de “largo alcance” y otras son “de corto alcance”. Para nuestros propósitos, realmente, la palabra “contacto” sólo será una especie de moniker conveniente, captador que usaremos para etiquetar los vectores de fuerza cuando nada más específico servirá.
1 El resultado (\ ref {eq:6.18}) generaliza a más dimensiones, pero para hacerlo correctamente se necesitan vectores y notación derivada parcial, y ya estoy doblando un poco las reglas notacionales aquí..
2 ¡Asumiendo que puedes comprimirlos! Algunos resortes, como los slinkies, en realidad no se pueden comprimir porque sus bobinas ya están en contacto cuando están relajadas. Sin embargo, la Ecuación (\ ref {eq:6.21}) seguirá aplicándose aproximadamente a dicho resorte cuando se estire, es decir, cuándo\(x>x_0\).


