6.3: Fuerzas no derivadas de una energía potencial
- Page ID
- 128122
Como hemos visto en el apartado anterior, para las interacciones que están asociadas a una energía potencial, siempre somos capaces de determinar las fuerzas a partir de la energía potencial por simple diferenciación. Esto significa que no tenemos que depender exclusivamente de una ecuación del tipo\(F = ma\), como (6.1.4) o (6.1.6), para inferir el valor de una fuerza a partir de la aceleración observada; más bien, podemos trabajar a la inversa, y predecir el valor de la aceleración (y de todo el movimiento posterior) de nuestro conocimiento de la fuerza.
He dicho antes que, a nivel microscópico, todas las interacciones pueden derivarse de energías potenciales, sin embargo, a nivel macroscópico esto no es generalmente cierto: tenemos muchos tipos de interacciones para las cuales la energía asociada “almacenada” o convertida no puede, en general, escribirse en función de la variables macroscópicas de posición para los objetos que componen el sistema (por lo que me refiero, típicamente, a las posiciones de sus centros de masa). Entonces, ¿qué hacemos en esos casos?
Las fuerzas de este tipo con las que trataremos este semestre realmente caen en dos categorías diferentes: las que no disipan energía, y que podríamos, de hecho, asociar con una energía potencial si quisiéramos 3, y las que definitivamente disipan energía y necesidad manejo especial. La primera categoría incluye la fuerza normal, la tensión y la fuerza de fricción estática; la segunda categoría incluye la fuerza de fricción cinética (o deslizante) y la resistencia al aire. A continuación se presenta una breve descripción de todas estas fuerzas, y los métodos para afrontarlas.
3 Si quisiéramos complicar nuestra vida, es decir...
Tensiones
La tensión es la fuerza ejercida por un resorte estirado y, de manera similar, por objetos como cables, cuerdas y cuerdas en respuesta a una fuerza de estiramiento (o carga) aplicada a ellos. En última instancia, es una fuerza elástica, así que, como dije anteriormente, podríamos en principio describirla por una energía potencial, pero en la práctica los cables, cuerdas y similares son tan rígidos que a menudo está bien descuidar su cambio de longitud por completo y asumir que ninguna energía potencial se almacena, de hecho, en ellos. El precio que pagamos por esta simplificación (y es una simplificación) es que nos quedamos sin una forma independiente de determinar el valor de la tensión en cualquier caso concreto; solo tenemos que inferirla de la aceleración del objeto sobre el que actúa (ya que es una fuerza de reacción, puede asumir cualquier valor que sea necesario para ajustarse a cualquier circunstancia, hasta el punto en que la cuerda se ajusta, de todos modos).
Así, por ejemplo, en la imagen de abajo, que muestra dos bloques conectados por una cuerda sobre una polea, la fuerza de tensión ejercida por la cuerda sobre el bloque 1 debe ser igual\(m_1a_1\), donde\(a_1\) está la aceleración de ese bloque, siempre que no haya otras fuerzas horizontales (como la fricción) que actúen sobre él. Para el bloque colgante, por otro lado, la fuerza neta es la suma de la tensión en el otro extremo de la cuerda (tirando hacia arriba) y la gravedad, tirando hacia abajo. Si elegimos la dirección ascendente como positiva, podemos escribir la segunda ley de Newton para el segundo bloque como
\[ F_{r, 2}^{t}-m_{2} g=m_{2} a_{2} \label{eq:6.22} .\]
Dos cosas necesitan ser realizadas ahora. Primero, si la cuerda es inextensible, ambos bloques recorren la misma distancia en el mismo tiempo, por lo que sus velocidades son siempre las mismas, y de ahí que la magnitud de sus aceleraciones siempre será la misma también; solo el signo puede ser diferente dependiendo de qué dirección elijamos como positiva. Si tomamos a la derecha para ser positivos para el movimiento horizontal, tendremos\(a_2 = −a_1\). Yo sólo voy a llamar\(a_1 = a\), entonces\(a_2 = −a\).
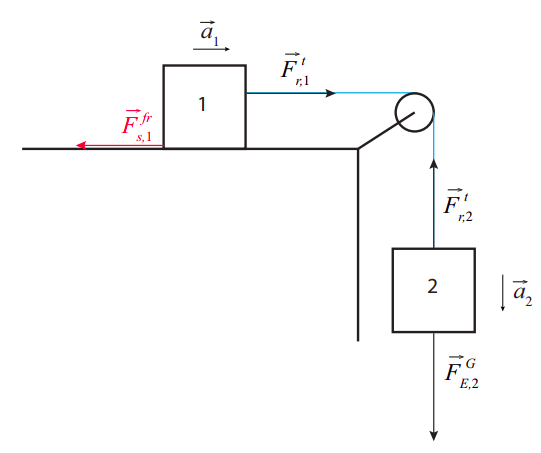
Lo segundo a tener en cuenta es que, si la masa de la cuerda es insignificante, ésta, como un resorte ideal, tirará con una fuerza con la misma magnitud en ambos extremos. Con nuestras elecciones específicas (arriba y a la derecha es positiva), entonces tenemos\(F^t_{r,2} = F^t_{r,1}\), y sólo voy a llamar a esta cantidad\(F^t\). Todo esto arroja, entonces, las siguientes dos ecuaciones:
\ begin {align}
F^ {t} &=m_ {1} a\ nonumber\\
F^ {t} -m_ {2} g &=-m_ {2} a\ label {eq:6.23}.
\ end {align}
El sistema (\ ref {eq:6.23}) se puede resolver fácilmente para obtener
\ begin {align}
a &=\ frac {m_ {2} g} {m_ {1} +m_ {2}}\ nonumber\\
F^ {t} &=\ frac {m_ {1} m_ {2} g} {m_ {1} +m_ {2}}\ etiqueta {eq:6.24}.
\ end {align}
Fuerzas normales
La fuerza normal es la fuerza de reacción con la que una superficie empuja hacia atrás cuando está siendo empujada. Nuevamente, esto funciona muy parecido a un resorte extremadamente rígido, esta vez bajo compresión en lugar de tensión. Y, nuevamente, evitaremos el tratamiento energético potencial asumiendo que el desplazamiento real de la superficie es completamente insignificante, y solo calcularemos el valor de\(F^n\) como lo que sea necesario para que la segunda ley de Newton funcione. Tenga en cuenta que esta fuerza siempre será perpendicular a la superficie, por definición (la palabra “normal” significa aquí “perpendicular”); la tarea de lidiar con un empuje lateral sobre la superficie se delegará a la fuerza de fricción estática, que se cubrirá a continuación.
Si solo estoy de pie en el suelo y no caigo por él, la fuerza vertical neta que actúa sobre mí debe ser cero. La fuerza de gravedad sobre mí es\(mg\) hacia abajo, y así la fuerza normal ascendente debe coincidir con este valor, así que para esta situación\(F^n = mg\). Pero no se apegen demasiado a la noción de que la fuerza normal siempre debe ser igual a\(mg\), ya que a menudo no será así. Imagínese, por ejemplo, a una persona parada dentro de un elevador en el momento en que está acelerando hacia arriba. Con la dirección ascendente como positiva, la segunda ley de Newton para la persona dice
\[ F^{n}-m g=m a \label{eq:6.25} \]
y por lo tanto para esta situación
\[ F^{n}=m g+m a \label{eq:6.26} .\]
Si te estuvieras pesando en una báscula de baño en el elevador, esta es la fuerza hacia arriba que la báscula de baño tendría que ejercer sobre ti, y lo haría comprimiendo un resorte dentro, y registraría la compresión “extra” (más allá de la requerida por tu peso real\(mg\)) como extra peso. Por el contrario, si el elevador estuviera acelerando hacia abajo, la báscula te registraría como más ligera. En el caso extremo en el que se rompió el cable del elevador y tú, el elevador y la báscula terminaron (brevemente, antes de que el freno de emergencia se prendiera) en caída libre, todos estarías cayendo con la misma aceleración, no estarías empujando hacia abajo en la báscula en absoluto, y su fuerza normal así como tu el peso registrado sería cero. Esta es en última instancia la razón de la aparente ingravidez que experimentan los astronautas en la estación espacial, donde la fuerza de la gravedad es, de hecho, no mucho menor que en la superficie de la tierra. (Volveremos a este efecto después de tener un buen control sobre el movimiento bidimensional, y en particular circular).
Fuerzas de fricción estáticas y cinéticas
La fuerza de fricción estática es una fuerza que evita que dos superficies en contacto se deslicen una respecto a la otra. Es una fuerza extremadamente útil, ya que no podríamos conducir un automóvil, ni andar en bicicleta, ni siquiera caminar, sin él, como sabemos por experiencia, si alguna vez hemos intentado hacer alguna de esas cosas en una superficie de baja fricción (como una capa de hielo).
La ciencia detrás de la fricción (conocida técnicamente como tribología) en realidad no es muy simple en absoluto, y es de gran interés actual por muchas razones, ya sea que el objetivo final sea desarrollar formas de reducir la fricción o aumentarla. A nivel elemental, todos somos conscientes de que incluso una superficie que se ve lisa a escala macroscópica en realidad exhibirá irregularidades, como crestas y valles, bajo un microscopio. Tiene sentido, entonces, que cuando dos de esas superficies son presionadas entre sí, los baches en una de ellas golpeen, y se sujeten en su lugar por, los baches en la otra, y eso evitará que se deslice hasta y a menos que se aplique una fuerza suficiente para “aplanar” temporalmente los baches lo suficiente como para permitir que la cosa se mueva 4.
Mientras esto no suceda, es decir, mientras las superficies no se deslicen una respecto a la otra, decimos que estamos lidiando con la fuerza de fricción estática, que es, al menos aproximadamente, una fuerza elástica que no disipa energía: la pequeña distorsión de los “golpes” en el las superficies que se producen cuando se empujan sobre ellas suelen suceder lo suficientemente lentamente, y es lo suficientemente pequeñas, para ser reversibles, de manera que cuando dejas de empujar las dos superficies solo tienes que volver a su estado inicial. Este ya no es el caso una vez que las superficies comienzan a deslizarse una respecto a la otra. En ese punto el carácter de la fuerza de fricción cambia, y tenemos que lidiar con la fuerza de fricción deslizante, o cinética, como explicaré a continuación.
La fuerza de fricción estática es también, como la tensión y la fuerza normal, una fuerza de reacción que se ajustará, dentro de límites, para tomar cualquier valor requerido para evitar el deslizamiento en una circunstancia dada. De ahí que su valor real en una situación particular no se pueda determinar realmente hasta que se conozcan las otras fuerzas relevantes —las otras fuerzas que empujan o tiran del objeto—.
Por ejemplo, para el sistema de la Figura\(\PageIndex{1}\), imagine que existe una fuerza de fricción estática entre el bloque 1 y la superficie sobre la que descansa, suficientemente grande como para evitar que se deslice por completo. ¿Qué tan grande tiene que ser esto? Si no hay aceleración (a = 0), el equivalente del sistema (\ ref {eq:6.23}) será
\ begin {align}
&F_ {s, 1} ^ {s} +F^ {t} =0\ nonumber\\
&F^ {t} -m_ {2} g=0\ label {eq:6.27}
\ end {align}
donde\(F^s_{s,1}\) esta la fuerza de fricción estática ejercida por la superficie sobre el bloque 1, y vamos a dejar que las matemáticas nos digan qué signo se supone que tiene. Resolviendo el sistema (\ ref {eq:6.27}) acabamos de obtener la condición
\[ F_{s, 1}^{s}=-m_{2} g \label{eq:6.28} \]
así que esto es lo grande que\(F^s_{s,1}\) tiene que ser para evitar que todo el sistema se mueva en este caso.
Existe una fórmula empírica que nos dice aproximadamente cuán grande puede llegar a ser la fuerza de fricción estática en una situación dada. La idea detrás de esto es que, microscópicamente, las superficies están en contacto sólo cerca de la parte superior de sus respectivas crestas. Si los presiona más fuerte, algunas de las crestas se aplanan y el área de contacto efectiva aumenta; esto a su vez hace que las superficies sean más resistentes al deslizamiento. Una medida directa de cuán fuertemente presionan las dos superficies una contra la otra es, en realidad, solo la fuerza normal que ejercen una sobre la otra. Entonces, en general, esperamos que la fuerza máxima que pueda ejercer la fricción estática sea proporcional a la fuerza normal entre las superficies:
\[ \left|F_{s 1, s 2}^{s}\right|_{\max }=\mu_{s}\left|F_{s 1, s 2}^{n}\right| \label{eq:6.29} \]
donde\(s_1\) y\(s_2\) solo significan “superficie 1" y “superficie 2", respectivamente, y el número\(\mu_s\) se conoce como el coeficiente de fricción estática: es una cantidad tabulada que se determina experimentalmente, probando el deslizamiento de diferentes superficies una contra la otra bajo diferentes cargas.
En nuestro ejemplo, la fuerza normal ejercida por la superficie sobre el bloque 1 tiene que ser igual a\(m_1g\), ya que no hay aceleración vertical para ese bloque, y así el valor máximo que\(F^s\) puede tener en este caso es\(\mu_sm_1g\), lo que\(\mu_s\) pueda suceder que sea. De hecho, esta configuración nos daría una forma de determinar\(\mu_s\) para estas dos superficies: comenzar con un pequeño valor de\(m_2\), y aumentarlo gradualmente hasta que el sistema comience a moverse. En ese punto sabremos que\(m_2g\) acaba de superar el máximo valor posible de\(\left|F^s_{12}\right|\), es decir,, y así\(\mu_sm_1g\)\(\mu_s = (m_2)_{max}/m_1\), dónde\((m_2)_{max}\) está la mayor masa que podemos colgar antes de que el sistema empiece a moverse.
En contraste con todo lo anterior, la fuerza de fricción cinética, que siempre actúa para oponerse al movimiento relativo de las dos superficies cuando realmente están deslizándose, no es elástica, definitivamente es disipativa y, lo más interesante, tampoco es mucha fuerza reactiva, lo que significa que su valor puede predecirse aproximadamente para cualquier circunstancia dada, y no depende mucho de cosas como la rapidez con la que las superficies se mueven realmente unas con respecto a otras. Depende de lo duro que estén presionando las superficies entre sí, cuantificado por la fuerza normal, y de otra cantidad tabulada conocida como coeficiente de fricción cinética:
\[ \left|F_{s 1, s 2}^{k}\right|=\mu_{k}\left|F_{s 1, s 2}^{n}\right| \label{eq:6.30} \]
Tenga en cuenta que, a diferencia de la fricción estática, este no es el valor máximo posible de\(F^k\) | |, sino su valor real; así que si sabemos\(F^n\) (y\(\mu_k\)) sabemos\(F^k\) sin tener que resolver ninguna otra ecuación (su signo sí depende de la dirección del movimiento, por supuesto) . El coeficiente\(\mu_k\) suele ser un poco menor que\(\mu_s\), reflejando el hecho de que una vez que obtienes algo has estado empujando para moverte, mantenerlo en movimiento con velocidad constante generalmente no requiere la misma cantidad de fuerza.
Para terminar con nuestro ejemplo en la Figura\(\PageIndex{1}\), supongamos que el sistema se está moviendo, y hay una fuerza de fricción cinética\(F^k_{s,1}\) entre el bloque 1 y la superficie. Las ecuaciones (\ ref {eq:6.23}) entonces tienen que cambiarse a
\ begin {align}
F^ {t} -\ mu_ {k} m_ {1} g &=m_ {1} a\ nonumber\\
F^ {t} -m_ {2} g &=-m_ {2} a\ label {eq:6.31}
\ end {align}
y la solución ahora es
Puede preguntarse, ¿por qué la fricción cinética disipa la energía? Una respuesta cualitativa es que, a medida que las superficies se deslizan una junto a la otra, sus pequeñas crestas (a veces microscópicas) se “topan” constantemente entre sí; así que tienes muchas colisiones microscópicas sucediendo todo el tiempo, y no todas pueden ser perfectamente elásticas. Entonces la energía mecánica se está “perdiendo”. De hecho, principalmente se está convirtiendo en energía térmica, como puedes verificar experimentalmente: es por eso que te frotas las manos para calentarte, por ejemplo. Más dramáticamente, así es como algunas personas (¡las que realmente saben lo que están haciendo!) en realidad puede iniciar un fuego frotando palos juntos.
4 Esta imagen basada, esencialmente, en la física clásica, deja de lado un efecto de escala atómica que puede ser importante en algunos casos, que es la formación de enlaces débiles entre los átomos de ambas superficies, dando como resultado una fuerza “adhesiva” real. Así es, por ejemplo, cómo los geckos pueden correr por muros verticales. Para nuestros propósitos, sin embargo, el cuadro clásico (de pequeñas crestas y valles chocando entre sí) bastará para entender cualitativamente todos los ejemplos que cubriremos este semestre.
Resistencia al aire
La resistencia al aire es una instancia de resistencia al fluido o arrastre, una fuerza que se opone al movimiento de un objeto a través de un fluido. Microscópicamente, se puede pensar en ello como debido a las constantes colisiones del objeto con las moléculas de aire, ya que se abre paso a través del aire. Como resultado de estas colisiones, parte de su impulso se transfiere al aire, así como parte de su energía cinética, que termina como energía térmica (como en el caso de la fricción cinética comentada anteriormente). Las temperaturas muy altas que puede generar la resistencia del aire se pueden ver, de una manera particularmente dramática, en la reentrada de naves espaciales a la atmósfera.
A diferencia de la fricción cinética entre superficies sólidas, la fuerza de arrastre del fluido depende de la velocidad del objeto (relativa al fluido), así como de una serie de otros factores que tienen que ver con la forma del objeto y la densidad y viscosidad del fluido. En términos muy generales, para velocidades bajas la fuerza de arrastre es proporcional a la velocidad del objeto, mientras que para velocidades altas es proporcional al cuadrado de la velocidad.
En principio, se puede usar la fórmula de arrastre adecuada junto con la segunda ley de Newton para calcular el efecto de la resistencia al aire sobre un simple objeto arrojado o caído; en la práctica, esto requiere una matemática algo más avanzada de lo que estaremos usando este curso, y las fórmulas en sí son complicadas, entonces yo no los introducirán aquí.
Un aspecto de la resistencia al aire que merece ser mencionado es lo que se conoce como “velocidad terminal” (que ya introduje brevemente en la Sección 2.3). Dado que la resistencia al aire aumenta con la velocidad, si sueltas un objeto desde una altura suficientemente grande, la fuerza de arrastre hacia arriba sobre él aumentará a medida que se acelera, hasta que en algún momento llegará a ser tan grande como la fuerza descendente de la gravedad. En ese punto, la fuerza neta sobre el objeto es cero, por lo que deja de acelerar, y a partir de ese punto sigue cayendo a velocidad constante. Cuando el filósofo griego Aristóteles intentaba averiguar el movimiento de los cuerpos que caían, razonó que, como el aire no era más que otro fluido, podía ralentizar la caída (para estudiarla mejor) sin cambiar la física al dejar caer objetos en líquidos en lugar de aire. El problema con este enfoque, sin embargo, es que la velocidad terminal se alcanza mucho más rápido en un líquido que en el aire, por lo que Aristóteles se perdió por completo la etapa inicial de aceleración aproximadamente constante, y concluyó (erróneamente) que la forma natural en que cayeron todos los objetos era con velocidad constante. Pasaron casi dos mil años hasta que Galileo desmintió esa noción al idear un mejor método para frenar el movimiento de caída, es decir, mediante el uso de planos inclinados.


