7.7: Ejemplos

Ejemplo\(\PageIndex{1}\): Braking

Supongamos que estás montando tu bicicleta y golpeas los frenos para llegar a un alto. Asumiendo que no hay deslizamiento entre la llanta y la carretera:

1. ¿Qué fuerza se encarga de quitar tu impulso? (Por “tú” me refiero a lo largo de “tú y la bicicleta”.)
2. ¿Qué fuerza se encarga de eliminar tu energía cinética?

Solución

a) Según lo que vimos en capítulos anteriores, por ejemplo, la Ecuación (6.1.10)

\ [\ frac {\ Delta p_ {\ text {sys}}} {\ Delta t} =F_ {\ text {ext, net}}\ label {eq:7.32}\]

el momento total del sistema solo puede ser cambiado por la acción de una fuerza externa, y la única fuerza externa disponible es la fuerza de fricción estática entre el neumático y la carretera (estática, porque asumimos que no hay deslizamiento). Entonces es esta fuerza la que quita el impulso hacia adelante del sistema. La distancia de parada\(\Delta x_{cm}\), y la fuerza, se pueden relacionar usando la Ecuación (7.3.1):

\ [F_ {r, t} ^ {s}\ Delta x_ {c m} =\ Delta K_ {c m}\ etiqueta {eq:7.33}.\]

(b) Ahora bien, aquí hay un dato interesante: la fuerza de fricción estática, aunque totalmente responsable de detener su centro de movimiento de masas no funciona en este caso. Eso se debe a que el punto donde se aplica —el punto del neumático que está momentáneamente en contacto con la carretera— también está momentáneamente en reposo con relación a la carretera: es, precisamente, no resbalar, entonces\(\Delta x\) en la ecuación\(W = F \Delta x\) es cero. Para cuando ese pedacito del neumático se haya movido, así que en realidad tienes un distinto de cero\(\Delta x\), ya no tienes un\(F\): la fuerza de fricción estática ya no está actuando sobre esa parte del neumático, está actuando sobre un bit diferente, sobre el que, de nuevo, no funcionará, por la misma razón.

Entonces, a medida que detenga su bicicleta el trabajo\(W_{ext,sys}\) = 0, y se deduce de la Ecuación (7.4.8) que la energía total de su sistema es, de hecho, conservada: toda su energía cinética inicial se convierte en energía térmica por la pastilla de freno frotando la rueda, y la fuerza interna responsable de esa conversión es la fuerza de fricción cinética entre la almohadilla y la rueda.

Ejemplo\(\PageIndex{2}\): Trabajo, energía y elección del sistema- caso disipativo

Consideremos nuevamente la situación que se muestra en la Figura 7.4.3. Dejar\(m_1\) = 1 kg,\(m_2\) = 2 kg, y\(\mu_k\) = 0.3. Utilizar las soluciones proporcionadas en la Sección 6.3 para calcular el trabajo realizado por todas las fuerzas, y los cambios en todas las energías, cuando el sistema sufre un desplazamiento de 0.5 m, y representar los cambios gráficamente usando diagramas de barras como los de la Figura 7.4.1 (para sistema A y B por separado)

Solución

De la Ecuación (6.3.11), tenemos

\ begin {align}
a &=\ frac {m_ {2} -\ mu_ {k} m_ {1}} {m_ {1} +m_ {2}} g=5.55\: \ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}}\ nonumber\\
F^ {t} &=\ frac {m_ {1} m_ {2}\ izquierda (1+\ mu_ {k}\ derecha)} {m_ {1} +m_ {2}} g=8.49\:\ mathrm {N}\ label {eq:7.34}
\ end {align}

Podemos usar la aceleración para calcular el cambio en la energía cinética, ya que tenemos la Ecuación (2.2.10) para movimiento con aceleración constante:

\ [v_ {f} ^ {2} -v_ {i} ^ {2} =2 a \ Delta x=2\ veces\ izquierda (5.55\: \ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}}\ derecha)\ veces 0.5\: \ mathrm {m} =5.55\:\ frac {\ mathrm {m} ^ {2}} {\ mathrm {s} ^ {2}} \ label {eq:7.35}\]

por lo que el cambio en la energía cinética de los dos bloques es

\ begin {align}
&\ Delta K_ {1} =\ frac {1} {2} m_ {1}\ izquierda (v_ {f} ^ {2} -v_ {i} ^ {2}\ derecha) =2.78\:\ mathrm {J}\ nonumber \\
&\ Delta K_ {2} =\ frac {1} {2} m_ {2}\ izquierda (v_ {f} ^ {2} -v_ {i} ^ {2}\ derecha) =5.55\:\ mathrm {J} \ label {eq:7.36}.
\ end {align}

También podemos usar la tensión para calcular el trabajo realizado por la fuerza externa en cada sistema:

\ begin {align}
W_ {e x t, A} &=F_ {r, 1} ^ {t}\ Delta x =( 8.49\:\ mathrm {N}) \ times (0.5\:\ mathrm {m}) =4.25\:\ mathrm {J}\ nonumber\\
W_ {e x t, B} &=F_ {r, 2} ^ {t}\ Delta y =( 8.49\:\ mathrm {N}) \ times (-0.5\:\ mathrm {m}) =-4.25\:\ mathrm {J}\ label {eq:7.37}.
\ end {align}

Por último, necesitamos el cambio en la energía potencial gravitacional del sistema B:

\ [\ Delta U_ {B} ^ {G} =m_ {2} g \ Delta y =( 2\:\ mathrm {kg})\ veces\ izquierda (9.8\: \ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}}\ derecha)\ veces (-0.5\: \ mathrm {m}) =-9.8\:\ mathrm {J}\ label {eq:7.38}\]

y el incremento de la energía disipada en el sistema A, que podemos obtener de la Ecuación (7.4.16):

\ [\ Delta E_ {\ text {diss}} =-F_ {s, 1} ^ {k}\ Delta x=\ mu_ {k} F_ {s, 1} ^ {n}\ Delta x=\ mu_ {k} m_ {1} g\ Delta x=0.3\ veces (1\:\ mathrm {kg}) \ veces\ izquierda (9.8\:\ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}}\ derecho) \ times (0.5\:\ mathrm {m}) =1.47\:\ mathrm {J}\ label {eq:7.39} .\]

Ahora podemos juntar todo esto para mostrar que la Ecuación (7.4.8) efectivamente sostiene:

\ begin {align}
W_ {e x t, A} &=\ Delta E_ {A} =\ Delta K_ {1} +\ Delta E_ {d i s s} =2.78\:\ mathrm {J} +1.47\:\ mathrm {J} =4.25\:\ mathrm {J} \ nonumber\\
W_ {e x t, B} &= Delta\ E_ {B} =\ Delta K_ {2} +\ Delta U_ {B} ^ {G} =5.55 \:\ mathrm {J} -9.8\:\ mathrm {J} =-4.25\:\ mathrm {J}\ etiqueta {eq:7.40} .
\ end {align}

Para trazar todo esto como barras energéticas, si no tienes acceso a un programa de dibujo muy preciso, normalmente tienes que hacer algunas aproximaciones. En este caso, vemos eso\(\Delta K_2 = 2\Delta K_1\) (exactamente), mientras que\ (\ Delta K_ {1}\ simeq 2\ Delta E_ {d i s s}\), así podemos usar una caja para representar\(E_{diss}\), dos cajas para\(\Delta K_1\), tres para \(W_{ext,A}\), cuatro para\(\Delta K_2\), y así sucesivamente. El resultado se muestra en verde en la imagen de abajo; las barras azules se han dibujado más exactamente a escala, y se muestran solo para su información.

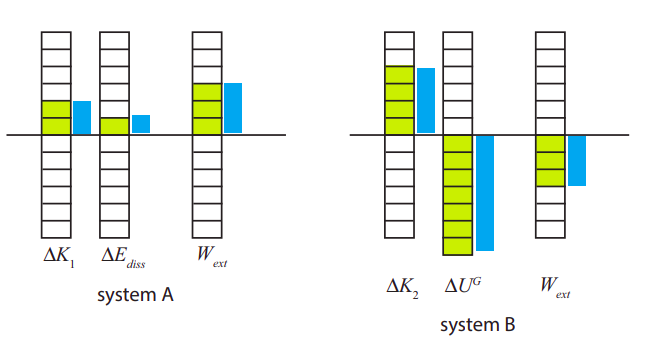
Ejemplo\(\PageIndex{3}\): Work, energía y la elección del sistema- caso no disipativo

Supongamos que cuelgas un resorte del techo, luego coloca un bloque al final del resorte y suelta. El bloque comienza a balancearse hacia arriba y hacia abajo en el muelle. Considera la hora inicial justo antes de soltarte, y la última vez en que el bloque se detiene momentáneamente en la parte inferior del columpio. Para cada una de las opciones de un sistema que se enumeran a continuación, encuentre el cambio neto de energía del sistema en este proceso, y relacionarlo explícitamente con el trabajo realizado en el sistema por una fuerza (o fuerzas) externas

1. El sistema es el bloque y el resorte.
2. El sistema es solo el bloque.
3. El sistema es el bloque y la tierra.

Solución

(a) El bloque por sí solo tiene energía cinética, y el resorte solo tiene energía potencial (elástica), por lo que la energía total de este sistema es la suma de estos dos. Para el intervalo considerado, el cambio en la energía cinética es cero, debido a que el bloque comienza y termina (momentáneamente) en reposo, por lo que solo cambia la energía del resorte. Esto tiene que ser igual al trabajo realizado por gravedad, que es la única fuerza externa.

Entonces, si el resorte se estira una distancia d, su energía potencial va de cero a \(\frac{1}{2}kd^2\), y el bloque cae a la misma distancia, así que la gravedad hace una cantidad de trabajo igual a\(mgd\), y tenemos

\ [W_ {g r a v} =m g d=\ Delta E_ {s y s} =\ Delta K+\ Delta U^ {s p r} =0+\ frac {1} {2} k d^ {2} \ etiqueta {eq:7.41}.\]

(b) Si el sistema es solo el bloque, la única energía que tiene es la energía cinética, la cual, como se indicó anteriormente, no ve un cambio neto en este proceso. Esto significa que el trabajo neto realizado en el bloque por las fuerzas externas debe ser cero. Las fuerzas externas en este caso son la fuerza del resorte y la gravedad, por lo que tenemos

\ [W_ {s p r} +W_ {g r a v} =\ Delta K=0\ etiqueta {eq:7.42}.\]

Hemos calculado\(W_{grav}\) anteriormente, así que a partir de esto obtenemos que el trabajo realizado por el resorte en el bloque, como se estira, es\(−mgd\), o (por Ecuación (\ ref {eq:7.41})) \(−\frac{1}{2}kd^2\). Tenga en cuenta que la fuerza ejercida por el resorte no es constante ya que se estira (o comprime) por lo que no podemos simplemente usar la Ecuación (7.2.1) para calcularla; más bien, necesitamos calcularla como una integral, como en la Ecuación (7.2.6), o derivarla de alguna manera indirecta como acabamos de hacer aquí.

(c) Si el sistema es el bloque y la tierra, tiene energía cinética y energía potencial gravitacional. La fuerza ejercida por el resorte es ahora una fuerza externa, por lo que tenemos:

\ [W_ {s p r} =\ Delta E_ {s y s} =\ Delta K+\ Delta U^ {G} =0-m g d\ etiqueta {eq:7.43}\]

así terminamos de nuevo con el resultado que\(W_{spr} = −mgd = −\frac{1}{2}kd^2\). Obsérvese que tanto el trabajo realizado por la primavera como el trabajo realizado por la gravedad son iguales a lo negativo de los cambios en sus respectivas energías potenciales, como deberían ser.

Ejemplo\(\PageIndex{4}\): Jumping

Para un salto de pie, comienzas de pie recto (A) de manera que el centro de masa de tu cuerpo esté a una altura \(h_1\) por encima del suelo. Luego dobla las rodillas para que su centro de masa esté ahora a una altura (inferior)\(h_2\) (B). Por último, enderezas las piernas, empujando con fuerza sobre el suelo, y despegas, así tu centro de masa termina por alcanzar una altura máxima,\(h_3\), por encima del suelo (C). Responde las siguientes preguntas con el mayor detalle que puedas.

1. Considera que el sistema es solo tu cuerpo. Al pasar de (A) a (B), ¿qué fuerzas externas están actuando sobre ella? ¿Cómo se comparan sus magnitudes, en función del tiempo?
2. Al pasar de (A) a (B), ¿alguna de las fuerzas que identificaste en la parte (a) funciona en tu cuerpo? Si es así, ¿cuál, y por cuánto? ¿La energía de tu cuerpo aumenta o disminuye como consecuencia de esto? ¿En qué tipo de energía crees que esta obra se convierte primordialmente?
3. Al pasar de (B) a (C), ¿qué fuerzas externas están actuando sobre ti? (No todos necesitan estar actuando todo el tiempo.) ¿Cómo se comparan sus magnitudes, en función del tiempo?
4. Al pasar de (B) a (C), ¿alguna de las fuerzas que identificaste funciona en tu cuerpo? Si es así, ¿cuál, y por cuánto? ¿La energía cinética de su cuerpo ve un cambio neto de (B) a (C)? ¿Qué otro cambio energético necesita tener lugar para que la Ecuación (7.4.8) (siempre con tu cuerpo como sistema) sea válida para este proceso?

Solución

(a) Las fuerzas externas sobre tu cuerpo son la gravedad, apuntando hacia abajo, y la fuerza normal desde el suelo, apuntando hacia arriba. Inicialmente, a medida que comienzas a bajar tu centro de masa, la fuerza normal tiene que ser ligeramente menor que la gravedad, ya que tu centro de masa adquiere una pequeña aceleración descendente. Sin embargo, eventualmente\(F^n\) tendría que superar\(F^G\) para detener el movimiento descendente.

(b) La fuerza normal no funciona, porque su punto de aplicación (las plantas de los pies) no se mueve, por lo que\(\Delta x\) en la expresión\(W = F\Delta x\) (Ecuación (7.2.1)) es cero.

La gravedad, por otro lado, hace un trabajo positivo, ya que siempre se puede tratar el centro de masa como el punto de aplicación de gravedad (ver Sección 7.3, nota al pie de página). Tenemos\(F^G_y = −mg\), y\ (\ Delta y = h_2 − h_1\), así

\ [W_ {g r a v} =F_ {y} ^ {G}\ Delta y=-m g\ izquierda (h_ {2} -h_ {1}\ derecha) =m g\ izquierda (h_ {1} -h_ {2}\ derecha) \ nonumber.\]

Dado que este es el trabajo neto realizado por todas las fuerzas externas sobre mi cuerpo, y es positivo, la energía total en mi cuerpo debe haber aumentado (por el teorema ((7.4.8)): \(W_{ext,sys} = \Delta E_{sys}\)). En este caso, es claro que el cambio principal tiene que ser un aumento en la energía potencial elástica de mi cuerpo, ya que mis músculos se tensan para el salto. (Un incremento en la energía térmica siempre es posible también.)

(c) Durante el salto, las fuerzas externas que actúan sobre mí son nuevamente la gravedad y la fuerza normal, que juntas determinan la aceleración de mi centro de masa. Al inicio del salto, la fuerza normal tiene que ser mucho más fuerte que la gravedad, para darme una gran aceleración hacia arriba. Como la fuerza normal es una fuerza de reacción, lo logro empujando muy fuerte con los pies en el suelo, a medida que extiendo los músculos de mis piernas: por la tercera ley de Newton, el suelo responde con una fuerza igual y opuesta hacia arriba.

A medida que mis piernas continúan estirándose, y se mueven hacia arriba, la fuerza que ejercen sobre el suelo disminuye, y también lo hace\(F^n\), que eventualmente se vuelve menor que\(F^G\). En ese punto (probablemente incluso antes de que mis pies abandonen el suelo) la aceleración de mi centro de masa se vuelve negativa (es decir, apuntando hacia abajo). Esto finalmente hace que mi movimiento hacia arriba se detenga, y mi cuerpo baje.

(d) La única fuerza que sí actúa sobre mi cuerpo durante el proceso descrito en (c) es la gravedad, ya que, nuevamente, el punto de aplicación de\(F^n\) es el punto de contacto entre mis pies y el suelo, y ese punto no se mueve hacia arriba ni hacia abajo —siempre está nivelado con el suelo. Entonces\ (W_ {ext, sys} = W_ {grav}\), que en este caso es realmente negativo:\(W_{grav} = −mg(h_3 − h_2)\).

Al pasar de (B) a (C), no hay cambio en tu energía cinética, ya que comienzas en reposo y terminas (momentáneamente) con velocidad cero en la parte superior del salto. Entonces el hecho de que haya un trabajo neto negativo hecho en ti significa que la energía dentro de tu cuerpo debe haber bajado. Claramente, algo de esto es solo una disminución en la energía potencial elástica. No obstante, dado que \(h_3\) (la altura final de tu centro de masa) es mayor que \(h_1\) (su altura inicial en (A), antes de agacharse), hay una pérdida neta de energía en tu cuerpo como resultado de todo el proceso. El lugar más obvio para buscar esta pérdida es en la energía química: “quemaste” algunas calorías en el proceso, principalmente al empujar con fuerza contra el suelo.