8.3: Planos Inclinados
- Page ID
- 128370
De vuelta en el Capítulo 2, declaré sin pruebas que la aceleración de un objeto que se deslizaba, sin fricción, por un plano inclinado haciendo un ángulo\(\theta\) con la horizontal era\(g \sin \theta\). Ahora puedo mostrarles por qué esto es así, e introducir la fricción también.
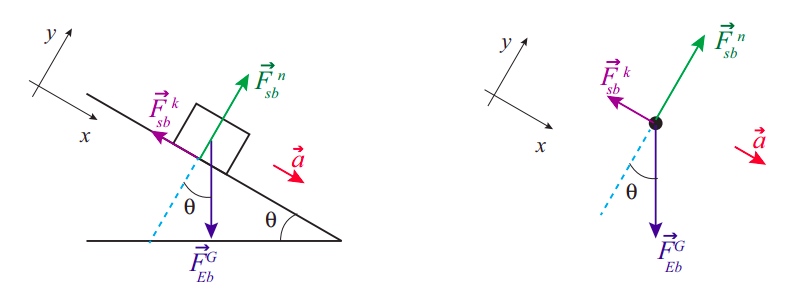
La figura\(\PageIndex{1}\) anterior muestra, a la izquierda, un bloque deslizándose por un plano inclinado y todas las fuerzas que actúan sobre él. Estos se ven más claramente en el diagrama de cuerpo libre a la derecha. He etiquetado todas las fuerzas usando la\(\vec{F}_{b y, o n}^{t y p e}\) convención introducida de nuevo en el Capítulo 6 (así, por ejemplo,\(\vec{F}_{sb}^{k}\) es la fuerza de fricción cinética ejercida por la superficie sobre el bloque); sin embargo, más adelante, para manipulaciones algebraicas, y especialmente dónde\(x\) y\(y\) componentes necesitan estar tomado, dejaré caer los subíndices “por, en”, y simplemente dejaré que el superíndice de “tipo” identifique la fuerza en cuestión.
Los diagramas también muestran los ejes de coordenadas que he elegido: el\(x\) eje está a lo largo del plano, y el\(y\) es perpendicular a él. La ventaja de esta elección es obvia: el movimiento es completamente a lo largo de uno de los ejes, y dos de las fuerzas (la fuerza normal y la fricción) ya se encuentran a lo largo de los ejes. La única fuerza que no lo hace es el peso del bloque (es decir, la fuerza de la gravedad), por lo que necesitamos descomponerlo en su\(x\) y\(y\) componentes. Para ello, podemos hacer uso del hecho, que se desprende de la geometría básica, que el ángulo de la inclinación,\(\theta\), es también el ángulo entre el vector\(\vec F^g\) y el\(y\) eje negativo. Esto significa que tenemos
\ begin {align}
&F_ {x} ^ {g} =F^ {g}\ sin\ theta\ nonumber\\
&F_ {y} ^ {g} =-F^ {g}\ cos\ theta\ label {eq:8.14}.
\ end {align}
Las ecuaciones (\ ref {eq:8.14}) también muestran otra convención que adoptaré a partir de ahora, es decir, que siempre que el símbolo para un vector se muestre sin una flecha en la parte superior \(x\)o un\(y\) subíndice, se entenderá que se refiere a la magnitud del vector, que es siempre un número positivo por definición.
La segunda ley de Newton, dada por las ecuaciones (8.2.1) aplicadas a este sistema, dice entonces:
\[ F_{x}^{g}+F_{x}^{k}=m a_{x}=F^{g} \sin \theta-F^{k} \label{eq:8.15} \]
para el movimiento a lo largo del plano, y
\[ F_{y}^{g}+F_{y}^{n}=m a_{y}=-F^{g} \cos \theta+F^{n} \label{eq:8.16} \]
para la dirección perpendicular al plano. Por supuesto, como no hay movimiento en esta dirección,\(a_y\) es cero. Esto nos da inmediatamente el valor de la fuerza normal:
\[ F^{n}=F^{g} \cos \theta=m g \cos \theta \label{eq:8.17} \]
ya que\(F^g = mg\). También podemos usar el resultado (\ ref {eq:8.17}), junto con la Ecuación (6.3.9), para obtener la magnitud de la fuerza de fricción, asumiendo que conocemos el coeficiente de fricción cinética (o deslizante),\(\mu_k\):
\[ F^{k}=\mu_{k} F^{n}=\mu_{k} m g \cos \theta \label{eq:8.18} .\]
Sustituyendo esto y\(F^G = mg\) en la Ecuación (\ ref {eq:8.15}), obtenemos
\[ m a_{x}=m g \sin \theta-\mu_{k} m g \cos \theta \label{eq:8.19} .\]
Podemos eliminar la masa para obtener finalmente
\[ a_{x}=g\left(\sin \theta-\mu_{k} \cos \theta\right) \label{eq:8.20} \]
que es el resultado deseado. A falta de fricción (\(\mu_k\)= 0) esto da\(a = g \sin \theta\), como lo tuvimos en el Capítulo 2. Tenga en cuenta que, si reduce la inclinación de la superficie (es decir, hacer\(\theta\) más pequeño), el\(\cos \theta\) término en Ecuación (\ ref {eq:8.20}) crece y el\(\sin \theta\) término se hace más pequeño, por lo que debemos asegurarnos de que no usamos esta ecuación cuando\(\theta\) es demasiado pequeña o obtendríamos el resultado absurdo de que\(a_x\) < 0, es decir, ¡que la fuerza de fricción cinética ha superado la gravedad y está acelerando el objeto hacia arriba!
Por supuesto, sabemos por experiencia que lo que sucede cuando\(\theta\) es muy pequeño es que el bloque no se desliza: se mantiene en su lugar por la fuerza de la fricción estática. El diagrama para tal situación se ve igual que Figura\(\PageIndex{1}\), excepto que\(\vec a\) = 0, la fuerza de fricción es\(F^s\) en lugar de\(F^k\), y por supuesto su magnitud debe coincidir con la del\(x\) componente de gravedad. La ecuación (\ ref {eq:8.15}) luego se convierte en
\[ m a_{x}=0=F^{g} \sin \theta-F^{s} \label{eq:8.21} .\]
Recordemos del Capítulo 6 que la fuerza de fricción estática no tiene un valor fijo: más bien, coincidirá con la fuerza aplicada hasta un valor máximo dado por la Ecuación (6.3.8):
\[ F_{\max }^{s}=\mu_{s} F^{n}=\mu_{s} m g \cos \theta \label{eq:8.22} \]
donde he usado la Ecuación (\ ref {eq:8.17}), ya que claramente la ecuación (\ ref {eq:8.16}) todavía se aplica a lo largo de la dirección vertical. Entonces, por un lado tenemos el requisito de que\(F^s = mg \sin \theta\) para evitar que el bloque se deslice, y por otro lado la restricción\(F^{s} \leq \mu_{s} m g \cos \theta\). Armando estos concluimos que el bloque no se deslizará siempre y cuando
\[ m g \sin \theta \leq \mu_{s} m g \cos \theta \label{eq:8.23} \]
o
\[ \tan \theta \leq \mu_{s} \label{eq:8.24} .\]
En definitiva, siempre y cuando\(\theta\) sea lo suficientemente pequeño como para satisfacer la Ecuación (\ ref {eq:8.24}), el bloque no se moverá. Una\(\theta\) vez superado el valor\(\tan ^{-1} \mu_{s}\), podemos aplicar el resultado (\ ref {eq:8.20}\)) para la aceleración. Tenga en cuenta que, como siempre tenemos\(\mu_{s} \geq \mu_{k}\), el resultado (\ ref {eq:8.20}) siempre será positivo si\(\theta>\tan ^{-1} \mu_{s}\), es decir, si\(\sin \theta>\mu_{s} \cos \theta\).
¿Y si enviamos el bloque deslizándose por el avión en su lugar? La aceleración seguiría apuntando hacia abajo (ya que el objeto estaría desacelerando todo el tiempo), pero ahora la fuerza de fricción cinética apuntaría en dirección opuesta a la indicada en la Figura\(\PageIndex{1}\), ya que siempre debe oponerse al movimiento. Si pasas por el mismo análisis que realicé anteriormente, lo conseguirás\(a_x = g (\sin \theta + \mu_k \cos \theta)\) en ese caso, ya que ahora la fricción y la gravedad están trabajando juntas para frenar la cámara.


