8.4: Movimiento en un Círculo (O Parte de un Círculo)
- Page ID
- 128358
El último ejemplo de movimiento en dos dimensiones que consideraré en este capítulo es el movimiento en círculo. Hay muchos ejemplos de movimiento circular (o casi circular) en la naturaleza, particularmente en astronomía (como veremos en un capítulo posterior, las órbitas de la mayoría de los planetas y muchos satélites son casi circulares). También hay muchos dispositivos que utilizamos todo el tiempo que involucran objetos giratorios o giratorios (ruedas, engranajes, plataformas giratorias, turbinas...). Todos estos pueden describirse matemáticamente como colecciones de partículas que se mueven en círculos.
En esta sección, primero introduciré el concepto de fuerza centrípeta, que es la fuerza necesaria para doblar la trayectoria de un objeto en un círculo (o un arco de círculo), y luego introduciré también una serie de cantidades que son útiles para la descripción del movimiento circular en general, como velocidad angular y aceleración angular. La dinámica del movimiento rotacional (preguntas que tienen que ver con la energía rotacional, y una nueva cantidad importante, el momento angular) serán el tema del siguiente capítulo.
Aceleración centrípeta y fuerza centrípeta
Como ya saben, la ley de inercia establece que, a falta de fuerzas externas, un objeto se moverá con velocidad constante en línea recta. Un círculo no es una línea recta, por lo que un objeto no seguirá naturalmente un camino circular a menos que haya una fuerza que actúe sobre él.
Otra forma de ver esto es volver a la definición de aceleración. Si un objeto tiene un vector de velocidad\(\vec v(t)\) en ese momento\(t\), y un vector de velocidad diferente\(\vec v(t + \Delta t)\) en el momento posterior\(t + \Delta t\), entonces su aceleración promedio a lo largo del intervalo de tiempo\(\Delta t\) es la cantidad\(\vec v_{av} = (\vec v(t + \Delta t) − \vec v(t))/ \Delta t\). Esto es distinto de cero aunque la velocidad no cambie (es decir, aunque los dos vectores de velocidad tengan la misma magnitud), siempre y cuando tengan direcciones diferentes, como puede ver en la Figura a\(\PageIndex{1}\) continuación. Así, el movimiento en un círculo (o un arco de círculo), incluso a velocidad constante, es un movimiento acelerado, y, según la segunda ley de Newton, el movimiento acelerado requiere de una fuerza para hacerlo realidad.
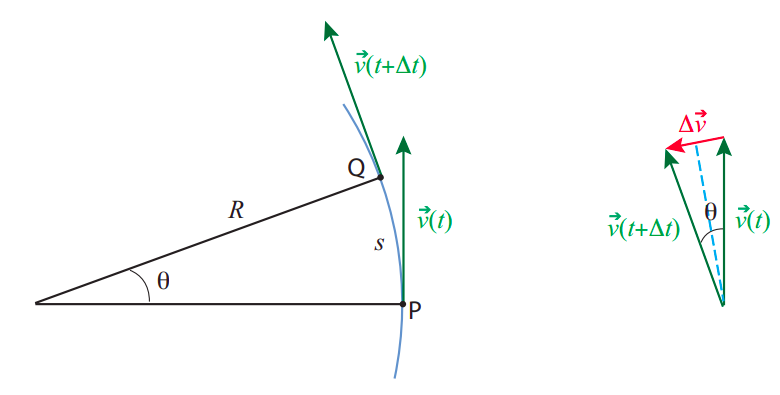
Podemos averiguar qué tan grande tiene que ser esta aceleración, y la fuerza asociada, aplicando un poco de geometría y trigonometría a la situación representada en la Figura\(\PageIndex{1}\). Aquí una partícula se mueve a lo largo de un arco de un círculo de radio\(r\), de manera que en su momento\(t\) está en el punto P y en el momento posterior\(t+ \Delta t\) está en el punto Q. La longitud del arco entre P y Q (la distancia que ha recorrido) es\(s = R\theta\), donde\(\theta\) se entiende que el ángulo está en radianes. He asumido que la velocidad es constante, por lo que la magnitud del vector de velocidad\(v\),, es igual a la relación de la distancia recorrida (a lo largo del círculo), al tiempo transcurrido:\(v = s/ \Delta t\).
A pesar de que la velocidad es constante, el movimiento se acelera, como acabo de decir anteriormente, porque la dirección del vector de velocidad cambia. El diagrama de la derecha muestra el vector de diferencia de velocidad\(\Delta \vec v = \vec v(t + \Delta t) − \vec v(t)\). Podemos obtener su longitud a partir de la trigonometría: si dividimos el ángulo\(\theta\) por la mitad, obtenemos dos triángulos rectos, y para cada uno de ellos\( |\Delta \vec{v}| / 2=v \sin (\theta / 2)\). Por lo tanto, tenemos
\[ \left|\vec{a}_{a v}\right|=\frac{|\Delta \vec{v}|}{\Delta t}=\frac{2 v \sin (\theta / 2)}{\Delta t} \label{eq:8.25} \]
para la magnitud del vector de aceleración promedio. La aceleración instantánea se obtiene tomando el límite de esta expresión como\(\Delta t \rightarrow 0\). En este límite, el ángulo\(\theta = s/R = v \Delta t/R\) se vuelve muy pequeño, y podemos usar la llamada “aproximación de ángulo pequeño”, que establece que\( \sin x \simeq x\) cuando\(x\) es pequeño y se expresa en radianes. Por lo tanto, por Ecuación (\ ref {eq:8.25}),
\[ \left|\vec{a}_{a v}\right|=\frac{2 v \sin (\theta / 2)}{\Delta t} \simeq \frac{v \theta}{\Delta t}=\frac{v^{2} \Delta t / R}{\Delta t} \label{eq:8.26} .\]
Esta expresión se vuelve exacta como\(\Delta t \rightarrow 0\), y luego se\(\Delta t\) cancela, mostrando que la aceleración instantánea tiene magnitud
\[ |\vec{a}|=a_{c}=\frac{v^{2}}{R} \label{eq:8.27} .\]
A esta aceleración se le llama aceleración centrípeta, razón por la cual la he denotado con el símbolo\(a_c\). El motivo de ese nombre es que siempre está apuntando hacia el centro del círculo. Puedes ver esto en la Figura\(\PageIndex{1}\): si tomas el vector que ahí\(\Delta \vec v\) se muestra, y lo mueves (sin cambiar su dirección, por lo que permanece 'paralelo a sí mismo”) al punto medio del arco, a medio camino entre los puntos P y Q, verás que sí apunta casi recto al centro del círculo. (Una prueba matemáticamente más rigurosa de este hecho, utilizando cálculo, se presentará en el siguiente capítulo, sección 9.3.)
La fuerza\(\vec F_c\) necesaria para proporcionar esta aceleración se llama la fuerza centrípeta, y por la segunda ley de Newton tiene que satisfacer\(\vec F_c = m\vec a_c\). Así, la fuerza centrípeta tiene magnitud
\[ F_{c}=m a_{c}=\frac{m v^{2}}{R} \label{eq:8.28} \]
y, al igual que la aceleración\(\vec a_c\), siempre se dirige hacia el centro del círculo.
Físicamente, la fuerza centrípeta\(F_c\), dada por la Ecuación (\ ref {eq:8.28}), es lo que se necesita para doblar la trayectoria para mantenerla precisamente en un arco de un círculo de radio\(R\) y con velocidad constante\(v\). Obsérvese que, dado que siempre\(\vec F_c\) es perpendicular al desplazamiento (que, en cualquier intervalo de tiempo corto, es esencialmente tangente al círculo), no trabaja sobre el objeto, y por lo tanto (por la Ecuación (7.2.8)) su energía cinética no cambia, así que\(v\) de hecho permanece constante cuando la fuerza centrípeta es igual a la fuerza neta. Tenga en cuenta también que “centrípeta” es solo una descripción del trabajo: no es un nuevo tipo de fuerza. En cualquier situación dada, el papel de la fuerza centrípeta lo jugará una de las fuerzas con las que ya estamos familiarizados, como la tensión sobre una cuerda (o un componente apropiado de la misma) cuando se está balanceando un objeto en un círculo horizontal, o la gravedad en el caso de la luna o cualquier otro satélite.
En este punto, si nunca antes has oído hablar de la fuerza centrípeta, es posible que te sientas un poco confundido, ya que casi con certeza has escuchado, en cambio, de una llamada fuerza centrífuga que tiende a alejar las cosas giratorias del centro de rotación. De hecho, sin embargo, esta “fuerza centrífuga” realmente no existe: la “fuerza” que puedes sentir empujándote hacia el exterior de una curva cuando conduces en un vehículo que da un giro brusco no es más que tu propia inercia: tu cuerpo “quiere” seguir moviéndose en línea recta, pero el auto, doblando su trayectoria, está impidiendo que así lo haga. La impresión que obtienes de que volarías radialmente hacia afuera, a diferencia de a lo largo de una tangente, también se debe completamente a que el marco de referencia en el que se encuentra (el automóvil) cambia continuamente su dirección de movimiento. Encontrarás este efecto ilustrado con cierto detalle en un ejemplo en la sección “Temas Avanzados”, si quieres verlo con más profundidad.
Por otro lado, conseguir que un automóvil negocie de manera segura un giro es en realidad un ejemplo importante de una situación que requiere de una fuerza centrípeta definida. Sobre una superficie plana (¡vea la sección “Temas Avanzados” para un tratamiento de una curva bancada!) , confías completamente en la fuerza de la fricción estática para mantenerte en la pista, que normalmente se puede modelar como un arco de círculo con cierto radio\(R\). Entonces, si estás viajando a una velocidad\(v\), necesitas\(F^s = mv^2/R\). Recordando que la fuerza de fricción estática no puede exceder\(\mu_sF^n\), y que sobre una superficie plana que solo tendrías\(F^n = F^g = mg\), ves que necesitas mantener\(mv^2/R\) más pequeña que\(\mu_{s}mg\); o, cancelando la masa,
\[ \frac{v^{2}}{R}<\mu_{s} g \label{eq:8.29} .\]
Esta es la condición que tiene que aguantar para poder realizar el giro de manera segura. La velocidad máxima es entonces\(v_{\max }=\sqrt{\mu_{s} g R}\), la cual, como se puede ver, dependerá del estado de la carretera (por ejemplo, si la carretera está mojada el coeficiente\(\mu_s\) será menor). La velocidad publicada y recomendada generalmente tomará esto en consideración y será tan baja como tiene que ser para mantenerte a salvo. Observe que el lado izquierdo de la Ecuación (\ ref {eq:8.29}) aumenta a medida que el cuadrado de la velocidad, ¡así que duplicar tu velocidad hace que ese término sea cuatro veces más grande! Ni siquiera pienses en dar un giro a 60 mph si la velocidad recomendada es de 30, y no superes la velocidad recomendada en absoluto si la carretera está mojada o tus llantas están desgastadas.
Variables angulares cinemáticas
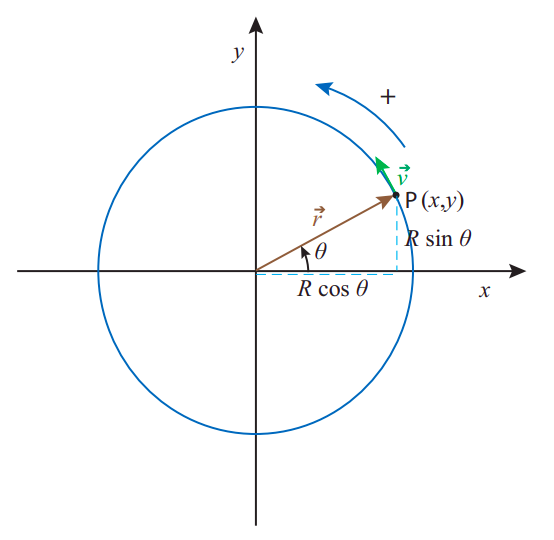
Considera que una partícula se mueve sobre un círculo, como en la Figura\(\PageIndex{2}\) a continuación. Por supuesto, solo podemos usar las coordenadas regulares, cartesianas,\(x\) y\(y\), para describir su movimiento. Pero, en cierto modo, esto está transportando más información de la que normalmente necesitamos, y tampoco es muy transparente: un valor de\(x\) y\(y\) no nos dice inmediatamente hasta qué punto ha viajado el objeto a lo largo del círculo mismo.
En cambio, la forma más conveniente de describir el movimiento de la partícula, si conocemos el radio del círculo, es dar el ángulo\(\theta\) que hace el vector de posición con algún eje de referencia en un momento dado, como se muestra en la Figura\(\PageIndex{2}\). Si elegimos el\(x\) eje como referencia, entonces la conversión de una descripción basada en el radio\(R\) y el ángulo\(\theta\) a una descripción en términos de\(x\) y\(y\) es simplemente
\ begin {align}
&x=R\ cos\ theta\ nonumber\\
&y=R\ sin\ theta\ label {eq:8.30}
\ end {align}
por lo que conociendo la función\(\theta (t)\) podemos obtener de inmediato\(x(t)\) y\(y(t)\), si las necesitamos. (Nota: en esta sección estoy usando una mayúscula\(R\) para la magnitud del vector de posición, para enfatizar que es una constante, igual al radio del círculo.)
Figura\(\PageIndex{2}\): Una partícula que se mueve sobre un círculo. El vector de posición tiene longitud\(R\), por lo que las\(y\) coordenadas\(x\) y son\(R \cos \theta\) y\(R \sin \theta\), respectivamente. Se indica la dirección positiva convencional del movimiento. El vector de velocidad es siempre, como de costumbre, tangente a la trayectoria.
Aunque el ángulo\(\theta\) en sí no es una cantidad vectorial, ni un componente de un vector, es conveniente permitir la posibilidad de que pueda ser negativo. La convención estándar es que\(\theta\) crece en el sentido contrario a las agujas del reloj desde el eje de referencia, y disminuye en el sentido de las agujas del reloj. Por supuesto, siempre se puede llegar a cualquier ángulo viniendo de cualquier dirección, así que el ángulo por sí mismo no te dice cómo llegó la partícula ahí. La información sobre la dirección del movimiento en un momento dado es mejor capturada por el concepto de la velocidad angular, que representamos por el símbolo\(\omega\) y definimos de manera análoga a la forma en que definimos la velocidad ordinaria: si\(\Delta \theta = \theta (t + \Delta t) − \theta (t)\) es el desplazamiento angular a lo largo de un tiempo \(\Delta t\), luego
\[ \omega=\lim _{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta t}=\frac{d \theta}{d t} \label{eq:8.31} .\]
La convención estándar también es usar radianes como medida de ángulo en este contexto, de manera que las unidades de\(\omega\) serán radianes por segundo, o rad/s. Tenga en cuenta que el radián es una unidad adimensional, por lo que “desaparece” de un cálculo cuando el resultado final no lo requiere (como en Ecuación (\ ref {eq:8.35}) a continuación).
La convención estándar también es usar radianes como medida de ángulo en este contexto, de manera que las unidades de\(\omega\) serán radianes por segundo, o rad/s. Tenga en cuenta que el radián es una unidad adimensional, por lo que “desaparece” de un cálculo cuando el resultado final no lo requiere (como en Ecuación (\ ref {eq:8.35}) a continuación).
Para el movimiento con velocidad angular constante, claramente tendremos
\[ \theta(t)=\theta_{i}+\omega\left(t-t_{i}\right) \quad \text { or } \quad \Delta \theta=\omega \Delta t \quad \text { (constant } \omega) \label{eq:8.32} \]
donde\(\omega\) es positivo para el movimiento antihorario y negativo para el sentido de las agujas del reloj. (Hay un sentido en el que es útil pensar en él\(\omega\) como un vector, pero, ya que no es inmediatamente obvio cómo o por qué, voy a posponer la discusión de este próximo capítulo, después de haber introducido el momento angular.)
Cuando\(omega\) cambia con el tiempo, podemos introducir una aceleración angular\(\alpha\), definida, nuevamente, de la manera obvia:
Entonces para el movimiento con aceleración angular constante tenemos las fórmulas
Las ecuaciones (\ ref {eq:8.32}) y (\ ref {eq:8.34}) son completamente paralelas a las ecuaciones correspondientes para movimiento en una dimensión que vimos en el Capítulo 1. De hecho, por supuesto, un círculo es solo una línea que se ha doblado de manera uniforme, por lo que la distancia recorrida a lo largo del círculo mismo es simplemente proporcional al ángulo barrido por el vector de posición\(\vec r\). Como ya se señaló en relación con la Figura\(\PageIndex{1}\), si\(\theta\) expresáramos en radianes entonces la longitud del arco correspondiente a un desplazamiento angular\(\Delta \theta\) sería
\[ s = R |\Delta \theta | \label{eq:8.35} \]
multiplicando así Eqs. (\ ref {eq:8.32}) o (\ ref {eq:8.34}) por da\(R\) directamente la distancia recorrida a lo largo del círculo en cada caso.
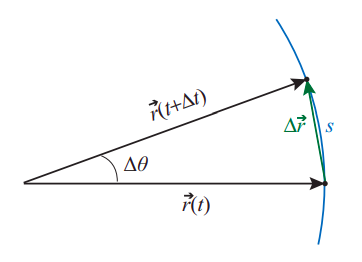
La figura\(\PageIndex{3}\) muestra que, para desplazamientos angulares muy pequeños, no importa si la distancia recorrida se mide a lo largo del círculo mismo o en línea recta; es decir,\(s \simeq|\Delta \vec{r}|\). Dividiendo por\(\Delta t\), usando la Ecuación (\ ref {eq:8.35}) y tomando el\(\Delta t \rightarrow 0\) límite obtenemos la siguiente relación útil entre la velocidad angular y la velocidad instantánea\(v\) (definida de la manera ordinaria como la distancia recorrida por unidad de tiempo, o la magnitud del vector de velocidad):
\[|\vec{v}|=R|\omega| \label{eq:8.36} .\]
Como veremos más adelante, el producto\(R\alpha\) es también una cantidad útil. No es, sin embargo, igual a la magnitud del vector de aceleración, sino solo uno de sus dos componentes, la aceleración tangencial:
\[ a_{t}=R \alpha \label{eq:8.37} .\]
La convención de signos aquí es que un positivo\(a_t\) representa un vector que es tangente al círculo y apunta en la dirección de aumento\(\theta\) (es decir, en sentido antihorario); el vector de aceleración completa es igual a la suma de este vector y el vector de aceleración centrípeta, introducido en la subsección anterior, que siempre apunta hacia el centro del círculo y tiene magnitud
\[ a_{c}=\frac{v^{2}}{R}=R \omega^{2} \label{eq:8.38} \]
(haciendo uso de Eqs. (\ ref {eq:8.29}) y (\ ref {eq:8.36})). Estos resultados se establecerán formalmente en el siguiente capítulo, después de que introduzcamos el producto vectorial, aunque también podrías verificarlos ahora mismo, si estás lo suficientemente familiarizado con los derivados en este punto, usando la regla de cadena para tomar las derivadas con respecto al tiempo de los componentes de la posición vector, como se da en la Ecuación (\ ref {eq:8.30}) (con\(\theta = \theta (t)\), una función arbitraria del tiempo).
Lo principal a recordar acerca de los componentes radial y tangencial de la aceleración es que el componente radial (la aceleración centrípeta) siempre está ahí para el movimiento circular, ya sea que la velocidad angular sea constante o no, mientras que la aceleración tangencial es solo distinta de cero si el la velocidad angular está cambiando, es decir, si la partícula se está desacelerando o acelerando a medida que gira.