8.7: Temas Avanzados

Ejemplo\(\PageIndex{1}\): Staying on track

(Este ejemplo estudia una situación que fácilmente podrías configurar experimentalmente en casa (¡puedes usar una esfera entera en lugar de una media esfera!) , aunque para que los números funcionen realmente necesitas asegurarte de que la fricción entre la superficie y el objeto que elijas sea realmente insignificante. Esencialmente se podría utilizar el mismo enfoque matemático para estudiar el problema de que un esquiador pase por encima de un magnate, o que un automóvil pierda contacto con la carretera si va demasiado rápido sobre una colina.)

Un objeto pequeño se coloca en la parte superior de una cúpula lisa (sin fricción) con forma de media esfera de radio\(R\), y se le da un pequeño empujón por lo que comienza a deslizarse hacia abajo de la cúpula, moviéndose inicialmente muy lentamente\(\left(v_{i} \simeq 0\right)\), pero recogiendo velocidad a medida que avanza, hasta que en algún momento vuela fuera de la superficie.

1. En ese punto, cuando el objeto pierde contacto con la superficie, ¿cuál es el ángulo que su vector de posición (con origen en el centro de la esfera) hace con la vertical?
2. ¿A qué distancia de la esfera aterriza el objeto?

Figura\(\PageIndex{1}\): Un objeto (bloque pequeño) que se desliza sobre una cúpula hemisférica. El dibujo (a) muestra el ángulo\(\theta_{max}\) en el que el objeto vuela (línea discontinua roja), y un ángulo genérico más pequeño\(\theta\). El dibujo (b) muestra el diagrama de cuerpo libre correspondiente al ángulo\(\theta\).

Solución

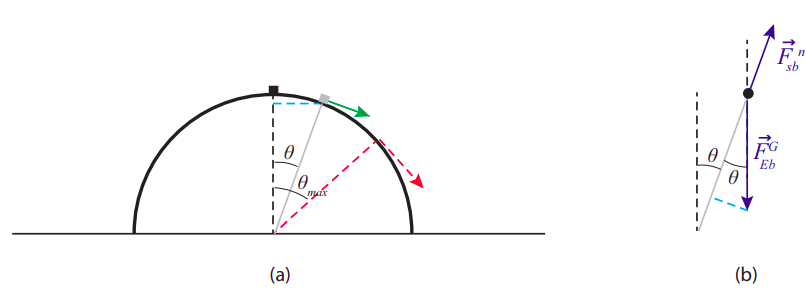
(a) Como vimos en la Sección 8.4, para que un objeto se mueva a lo largo de un arco de círculo,\(mv^2/r\) se requiere una fuerza centrípeta de magnitud. Mientras nuestro objeto esté en contacto con la superficie, las fuerzas que actúan sobre él son la fuerza normal (que apunta a lo largo de la dirección radial, por lo que hace una contribución negativa a la fuerza centrífuga) y la gravedad, que tiene un componente\(mg \cos \theta\) a lo largo del radio, hacia el centro del círculo (ver Figura\(\PageIndex{1}\) (b), la línea azul claro discontinua). Entonces, la ecuación de fuerza centrípeta dice

\[ \frac{m v^{2}}{R}=m g \cos \theta-F^{n} \label{eq:8.46} .\]

Lo siguiente que tenemos que hacer es encontrar el valor de la velocidad v para un ángulo dado\(\theta\). Si tratamos el objeto como una partícula, su única energía es la energía cinética, y\(\Delta K = W_{net}\) (Ecuación (7.2.8)), donde\(W_{net}\) está el trabajo realizado sobre la partícula por la fuerza neta que actúa sobre ella. La fuerza normal siempre es perpendicular al desplazamiento, por lo que no hace trabajo, mientras que la gravedad siempre es vertical y sí funciona\(W_{grav} = −mg\Delta y\) (tomando hacia arriba como positivo, por lo que\(\Delta y\) es negativo). De hecho, de la Figura\(\PageIndex{1}\) (a) (siga la línea azul discontinua) se puede ver que para un ángulo dado\(\theta\), la altura del objeto sobre el suelo es\(R \cos \theta\), por lo que el desplazamiento vertical desde su posición inicial es

\[ \Delta y=-(R-R \cos \theta) \label{eq:8.47} \]

De ahí que tengamos, para el cambio en la energía cinética,

\[ \frac{1}{2} m v^{2}-\frac{1}{2} m v_{i}^{2}=m g R-m g R \cos \theta \label{eq:8.48} .\]

Suponiendo, como nos dicen en el texto del problema, eso\(v_{i} \simeq 0\), obtenemos\(v^2 \simeq 2gR − 2gR \cos \theta \), y usando esto en Ecuación (\ ref {eq:8.46})

\[ 2 m g-2 m g \cos \theta=m g \cos \theta-F^{n} \label{eq:8.49} \]

o\(F^n = 3mg \cos \theta −2mg\). Esto muestra que\(F^n\) comienza (cuando\(\theta\) = 0) teniendo su valor habitual de\(mg\), y luego se vuelve progresivamente más pequeño a medida que el objeto se desliza hacia abajo. El punto donde el objeto pierde contacto con la superficie es cuando\(F^n\) = 0, y eso sucede para

\[ 3 \cos \theta_{max} = 2 \label{eq:8.50} \]

o\(\theta_{\max }=\cos ^{-1}(2 / 3)=48.2^{\circ} \).

Recordando eso\(\Delta y = −(R − R \cos \theta)\), vemos que cuando\( \cos \theta\) = 2/3, el objeto ha caído una distancia\(R\) /3; puesto de lo contrario, su altura sobre el suelo en el momento en que sale volando es de 2\(R\) /3, o 2/3 de la altura inicial.

(b) Esto es sólo un problema de proyectiles ahora. Solo tenemos que encontrar los valores de las condiciones iniciales (\(x_i\),\(y_i\),\(v_{x,i}\) y\(v_{y,i}\)) y sustituirlos en las ecuaciones (8.2.2). Al inspeccionar la figura, se puede ver que, en el momento en que el objeto vuela,

\ begin {align}
&x_ {i} =R\ sin\ theta_ {\ max} =0.745 R\ nonumber\\
&y_ {i} =R\ cos\ theta_ {\ max} =0.667 R\ label {e:8.51}.
\ end {align}

También, encontramos por encima de eso\(v^{2} \simeq 2 g R-2 g R \cos \theta\), y cuando\(\theta = \theta_{max}\) esto da\(v^2 = 0.667gR\), o\(v=0.816 \sqrt{g R} \). El ángulo de proyección en este caso es\(−\theta_{max}\); es decir, la velocidad inicial del proyectil (flecha roja discontinua en la Figura\(\PageIndex{1}\) (a)) está en un ángulo 48.2 por\(^{\circ}\) debajo del\(x\) eje positivo, por lo que tenemos:

\ begin {align}
&v_ {x, i} =v_ {i}\ cos\ theta_ {\ max} =0.544\ sqrt {g R}\ nonumber\\
&v_ {y, i} =-v_ {i}\ sin\ theta_ {\ max} =-0.609\ sqrt {g R}\ etiqueta {eq:8.52}
\ fin alinear}

Ahora solo usamos estos resultados en Eqs. (8.2.2). En concreto, queremos saber cuánto tiempo tarda el objeto en llegar al suelo, así que usamos la última ecuación (8.2.2) con\(y\) = 0 y resolvemos para\(t\):

\[ 0=y_{i}+v_{y, i} t-\frac{1}{2} g t^{2} \label{eq:8.53} \]

El resultado es\(t=0.697 \sqrt{R / g}\). (No es necesario llevar el “\(g\)” a lo largo; estaría bien sustituirlo 9.8 m/s ² por él. Acabo de mantenerlo en forma simbólica hasta el momento para dejar claro que las cantidades que derivemos tendrán las unidades adecuadas). Sustituyendo esto en la ecuación por\(x\), obtenemos

\[ x=x_{i}+v_{x, i} t=0.745 R+0.544 \sqrt{g R} \times 0.697 \sqrt{R / g}=1.125 R \label{eq:8.54} \]

(¡Tenga en cuenta cómo se\(g\) cancela, así que obtendríamos el mismo resultado en cualquier planeta!) Dado que la esfera tiene un radio\(R\), el objeto cae a cierta\(0.125R\) distancia de la esfera.

Ejemplo\(\PageIndex{2}\): Going around a banked curve

Los ingenieros de carreteras suelen tener una curva, especialmente si se trata de un giro muy apretado, por lo que los autos no tendrán que depender solo de la fricción para proporcionar la fuerza centrípeta requerida. La imagen muestra un automóvil dando la vuelta a una curva de este tipo, que podemos modelar como un arco de un círculo de radio\(r\). En términos de\(r\), el ángulo de inclinación\(\theta\), y el coeficiente de fricción estática, encuentran la velocidad máxima segura alrededor de la curva.

Figura\(\PageIndex{2}\): Un automóvil que gira alrededor de una curva bancada (boceto y diagrama de cuerpo libre). El centro del círculo está hacia la derecha.

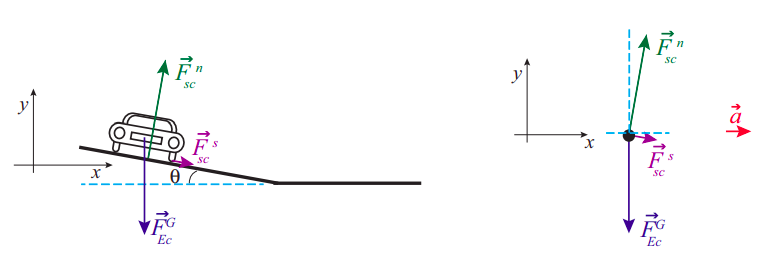
En la figura se muestra la elección adecuada de los ejes para este problema. El criterio es, nuevamente, elegir los ejes para que uno de ellos coincida con la dirección de la aceleración. En este caso, la aceleración es toda centrípeta, es decir, apuntando, horizontalmente, hacia el centro del círculo sobre el que viaja el automóvil.

Puede parecer extraño ver la fuerza de fricción estática apuntando por la pendiente, pero recordemos que para un automóvil que gira sobre una superficie plana habría estado apuntando hacia adentro (hacia el centro del círculo), por lo que esta es la extensión natural de eso. En general, siempre se debe tratar de imaginar en qué dirección se deslizaría el objeto si la fricción desapareciera por completo:\(\vec F^s\) debe apuntar en la dirección opuesta a esa. De esta manera, para un automóvil que viaja a una velocidad razonable, la dirección en la que patinaría es arriba de la pendiente, y eso significa que\(\vec F^s\) debe apuntar hacia abajo por la pendiente. Pero, para un automóvil simplemente sentado quieto en la carretera inclinada,\(\vec F^s\) hay que apuntar hacia arriba, y veremos en un momento que en general se requiere una velocidad mínima para que la fuerza de fricción estática apunte en la dirección que hemos elegido.

Aparte de esto, la principal diferencia con la caja de superficie plana es que ahora la fuerza normal tiene un componente a lo largo de la dirección de la aceleración, por lo que ayuda a mantener el automóvil moviéndose en círculo. Por otro lado, tenga en cuenta que ahora perdemos (para fines centrípetos) un poco de la fuerza de fricción, ya que está apuntando ligeramente hacia abajo. Esto, sin embargo, está más que compensado por el hecho de que la fuerza normal es mayor ahora de lo que sería para una superficie plana, ya que el automóvil está ahora, por así decirlo, “conduciendo” un poco hacia la carretera.

Las líneas azules discontinuas en el diagrama de cuerpo libre están destinadas a indicar que el ángulo\(\theta\) del banco es también el ángulo entre la fuerza normal y el\(y\) eje positivo, así como el ángulo que\(\vec F^s\) hace por debajo del\(x\) eje positivo. De ello se deduce que los componentes de estas dos fuerzas a lo largo de los ejes mostrados son:

\ begin {align}
&F_ {x} ^ {n} =F^ {n}\ sin\ theta\ nonumber\\
&F_ {y} ^ {n} =F^ {n}\ cos\ theta\ etiqueta {eq:8.55}
\ end {align}

y

\ begin {align}
&F_ {x} ^ {s} =F^ {s}\ cos\ theta\ nonumber\\
&F_ {y} ^ {n} =-F^ {s}\ sin\ theta\ etiqueta {eq:8.56}
\ end {align}

La ecuación de fuerza vertical es entonces:

\[ 0=m a_{y}=F_{y}^{n}+F_{y}^{s}-F^{G}=F^{n} \cos \theta-F^{s} \sin \theta-m g \label{eq:8.57} .\]

Esto demuestra que efectivamente\(F^n = (mg + F^s \sin \theta)/ \cos \theta \) es mayor que solo\(mg\) para este problema, y debe aumentar a medida que\(\theta\) aumenta el ángulo (ya que\(\cos \theta\) disminuye con el aumento\(\theta\)). La ecuación horizontal es:

\[ m a_{x}=F_{x}^{n}+F_{x}^{s}=F^{n} \sin \theta+F^{s} \cos \theta=\frac{m v^{2}}{r} \label{eq:8.58} \]

donde ya he sustituido el valor de la aceleración centrípeta por\(a_x\). Las ecuaciones (\ ref {eq:8.57}) y (\ ref {eq:8.58}) forman un sistema que necesita ser resuelto para las dos incógnitas\(F^n\) y\(F^s\). El resultado es:

\ begin {align}
&F^ {n} =m g\ cos\ theta+\ frac {m v^ {2}} {r}\ sin\ theta\ nonumber\\
&F^ {s} =-m g\ sin\ theta+\ frac {m v^ {2}} {r}\ cos\ theta\ label {eq:8.59}.
\ end {align}

Obsérvese que la segunda ecuación\(F^s\) se habría vuelto negativa si\( v^{2}<g r \tan \theta \). Esto significa que por debajo de esa velocidad, la fuerza de fricción estática debe apuntar realmente hacia arriba de la pendiente, como se discutió anteriormente. Podemos llamar a esta velocidad particular, para la cual\(F^s\) se convierte en cero,\(v_{no \: friction}\):

\[ v_{\text {no friction }}=\sqrt{g r \tan \theta} \label{eq:8.60} .\]

Lo que esto significa es que es posible disponer el ángulo de inclinación para que un automóvil que vaya a una velocidad específica no tenga que depender en absoluto de la fricción para hacer la curva: la fuerza normal sería la justa para proporcionar la aceleración centrípeta requerida. Un auto que iba a esa velocidad no se sentiría ni tirado hacia abajo ni empujado por la pendiente. Sin embargo, un automóvil que va más rápido que eso tendería a “volar”, y se requeriría la fuerza de fricción estática para jalarlo y mantenerlo en la curva, mientras que un automóvil que se mueve más lentamente tendería a deslizarse hacia abajo y tendría que ser empujado hacia arriba por la fuerza de fricción. La fricción, por lo tanto, proporciona un rango de velocidades seguras para conducir en este caso, tal como lo hizo en la caja de superficie plana.

Podemos calcular la velocidad máxima segura como lo hacíamos antes, recordando que siempre debemos tener\(F^{s} \leq \mu_{s} F^{n}\). Sustitución de Eqs. (\ ref {eq:8.59}) en esta expresión, y resolviendo para\(v\), obtenemos la condición

\[ v_{\max }=\sqrt{g r} \sqrt{\frac{\mu_{s}+\tan \theta}{1-\mu_{s} \tan \theta}} \label{eq:8.61} .\]

Esto reproduce nuestro resultado (8.4.5) para\(\theta\) = 0 (un camino plano), como debería.

Para poner algunos números en esto, supongamos que la curva tiene un radio de 20 m, y el coeficiente de fricción estática entre las llantas y la carretera es\(\mu_s\) = 0.7. Entonces, para una superficie plana, obtenemos\(v_{max}\) = 11.7 m/s, o aproximadamente 26 mph, mientras que para un ángulo de inclinación de\(\theta\) = 10\(^{\circ}\) (el ángulo elegido para la figura anterior) obtenemos\(v_{max}\) = 14 m/s, o aproximadamente 31 mph.

La ecuación (\ ref {eq:8.61}) en realidad indica que la velocidad máxima “se volvería infinita” para un ángulo de inclinación finito, es decir\(1 − \mu_s \tan \theta = 0\), si, o\(\tan \theta = 1/ \mu_s\) (si\(\mu_s\) = 0.7, esto corresponde a\(\theta\) = 55\(^{\circ}\)). Esto es matemáticamente correcto, pero claro que no podemos tomarlo literalmente: asume que no hay límite a cuán grande puede ejercer una fuerza normal que pueda ejercer la calzada sin sufrir daños, y también que\(F^s\) puede llegar a ser arbitrariamente grande mientras permanezca por debajo del límite\(F^{s} \leq \mu_{s} F^{n} \). Ninguno de estos supuestos se sostendría en la vida real para velocidades muy grandes. Además, el ángulo\(\theta=\tan ^{-1}\left(1 / \mu_{s}\right) \) es demasiado empinado: recordemos que, de acuerdo con la Ecuación (8.3.11), la fuerza de fricción sólo podrá evitar que un objeto (inicialmente en reposo) se deslice por la pendiente si\(\tan \theta \leq \mu_{s}\), que para\(\mu_s\) = 0.7 medias\(\theta \leq 35^{\circ}\). Entonces, con un ángulo de inclinación de 55\(^{\circ}\) podrías conducir en la curva, siempre que fueras lo suficientemente rápido, pero no podrías estacionar en él, ¡el auto se deslizaría hacia abajo! En pocas palabras, use Ecuación (\ ref {eq:8.61}) solo para valores moderados de\(\theta\)... y no exceda\(\theta=\tan ^{-1} \mu_{s}\) si desea que un automóvil pueda conducir alrededor de la curva lentamente sin deslizarse hacia abajo en la zanja.

Ejemplo\(\PageIndex{3}\): Rotating frames of reference- centrifugal force and coriolis force

Imagina que estás dentro de una habitación cilíndrica giratoria de radio\(R\). Hay un disco metálico en el piso, a una\(r\) distancia del eje de rotación, sostenido en su lugar con un electroimán. En algún momento se apaga el electroimán y el disco queda libre de deslizarse sin fricción. Encuentra dónde golpea el disco contra la pared, y demuestra que, si no estaba muy lejos de la pared para empezar, parece como si se hubiera movido recto hacia la pared en cuanto se soltó.

Solución

La imagen se ve como se muestra a continuación, a un observador en un marco inercial, mirando hacia abajo. El disco inicia en el punto A, con velocidad instantánea\(\omega r\) apuntando recto hacia la izquierda en el momento en que se suelta, por lo que simplemente se mueve recto (en el marco inercial) hasta que golpea la pared en el punto B. Del triángulo color cián mostrado, podemos ver que recorre una distancia\(\sqrt{R^{2}-r^{2}}\), lo que lleva un tiempo

\[ \Delta t=\frac{\sqrt{R^{2}-r^{2}}}{\omega r} \label{eq:8.62} .\]

En este tiempo, la habitación gira en sentido contrario a las agujas del reloj en un ángulo\(\Delta \theta_{room} = \omega \Delta t\):

\[ \Delta \theta_{\text {room}}=\frac{\sqrt{R^{2}-r^{2}}}{r} \label{eq:8.63} .\]

Figura\(\PageIndex{3}\): El movimiento del disco (cian) y la pared (magenta) visto por un observador inercial.

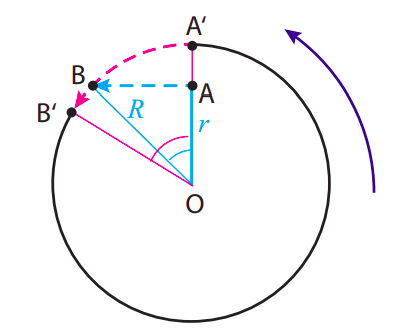
Este es el ángulo que se muestra en magenta en la figura. Como resultado de esta rotación, el punto A\(^{\prime}\) que inicialmente estaba en la pared recto frente al disco se ha movido (siguiendo la línea discontinua magenta) a la posición B\(^{\prime}\), por lo que a un observador en la sala giratoria, mirando las cosas desde el punto O, el disco parece dirigirse hacia la pared y deriva un poco a la derecha mientras lo hace.

El ángulo cian en la imagen, que podríamos llamar\(\Delta \theta_{part}\), tiene tangente igual a\(\sqrt{R^{2}-r^{2}} / r\), así que tenemos

\[ \Delta \theta_{\text {room}}=\tan \left(\Delta \theta_{\text {part}}\right) \label{eq:8.64} .\]

Esto nos dice que los dos ángulos van a estar bastante cerca si son lo suficientemente pequeños, que es lo que sucede si el disco comienza lo suficientemente cerca de la pared en primer lugar. La imagen muestra, para mayor claridad, el caso cuando\(r = 0.7R\), lo que da\(\Delta \theta_{room}\) = 1.02 rad, y\(\Delta \theta_{part} = \tan^{−1}(1.02)\) = 0.8 rad. Porque\(r = 0.9R\), por otro lado, se encuentra\(\Delta \theta_{room}\) = 0.48 rad, y\(\Delta \theta_{part} = \tan^{−1}\) (0.48) = 0.45 rad.

En términos de pseudofuerzas (fuerzas que no existen físicamente, sino que pueden introducirse para describir matemáticamente el movimiento de los objetos en marcos de referencia no inerciales), el observador no inercial diría que el disco se dirige hacia la pared debido a una fuerza centrífuga (es decir, una fuerza apuntando alejándose del centro de rotación), y al hacerlo deriva hacia la derecha debido a la llamada fuerza Coriolis.