11.2: Movimiento armónico simple
- Page ID
- 128053
Un tipo particularmente importante de movimiento oscilatorio se llama movimiento armónico simple. Esto es lo que sucede cuando la fuerza restauradora es lineal en el desplazamiento desde la posición de equilibrio: es decir, en una dimensión, si\(x_0\) es la posición de equilibrio, la fuerza restauradora tiene la forma
\[ F=-k\left(x-x_{0}\right) \label{eq:11.2} .\]
Estamos familiarizados con esto de la “ley” de Hooke para una primavera ideal (ver Capítulo 6). Entonces, un objeto unido a un resorte ideal, sin masa, como en la siguiente figura, debe realizar un movimiento armónico simple. Este tipo de oscilación se distingue por las siguientes características:
- La posición en función del tiempo,\(x(t)\), es una función sinusoidal.
- El periodo de las oscilaciones no depende de su amplitud (por “amplitud” nos referimos al desplazamiento máximo desde la posición de equilibrio).
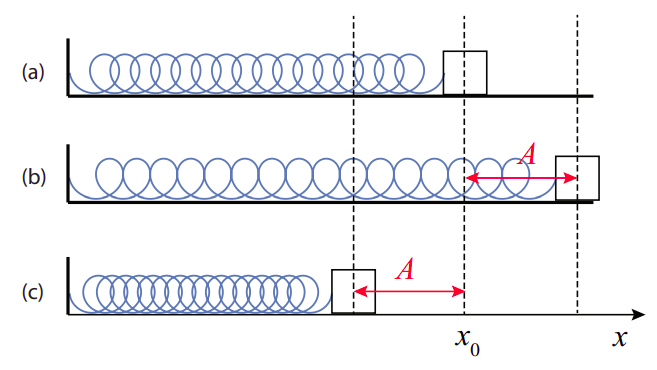
Lo que significa esta segunda propiedad es que, por ejemplo, con referencia a la Figura\(\PageIndex{1}\), se puede desplazar la masa a una distancia\(A\)\(A/2\), o\(A/3\), o, o lo que elija, y el periodo (y frecuencia) de las oscilaciones resultantes será el mismo independientemente. (Esto significa, en realidad, que si lo desplazas más lejos tiene que terminar moviéndose más rápido, para cubrir la mayor distancia al mismo tiempo.)
Como sabemos que “la ley de Hooke” es en realidad solo una aproximación, válida solo siempre que el resorte no esté comprimido o estirado demasiado, esperamos que en la vida real las propiedades de movimiento armónico simples “ideales” que he enumerado anteriormente solo se mantengan aproximadamente, también; así, de hecho, si estiras un resorte demasiado obtendrás un periodo diferente, eventualmente, que si te quedas en el régimen jurídico “lineal” de Hooke. Esta es una característica general de la mayoría de los sistemas físicos: el movimiento armónico simple solo ocurre para oscilaciones relativamente pequeñas, pero “relativamente pequeñas” todavía puede ser bastante grande a veces, e incluso como aproximación suele ser extremadamente valioso.
La otra característica distintiva del movimiento armónico simple es que la función de posición es sinusoidal, con lo que me refiero a un seno o un coseno. Así, por ejemplo, si la masa en la Figura\(\PageIndex{1}\) se libera del reposo en\(t\) = 0, y la posición\(x\) se mide desde la posición de equilibrio\(x_0\) (es decir, el punto\(x = x_0\) se toma como origen de coordenadas), la función\(x(t)\) será
\[ x(t)=A \cos (\omega t) \label{eq:11.3} \]
donde la cantidad\(\omega\), conocida como frecuencia angular del oscilador, viene dada por
\[ \omega=\sqrt{\frac{k}{m}} \label{eq:11.4} .\]
Aquí,\(k\) es la constante de resorte, y\(m\) la masa del objeto (recuerde que se supone que el resorte es sin masa). Voy a probar que la Ecuación (\ ref {eq:11.3}), junto con (\ ref {eq:11.4}), satisfacen en un momento la segunda ley del movimiento de Newton para este sistema; primero, sin embargo, necesito decir un par de cosas al respecto\(\omega\). Recordarás que hemos usado este símbolo antes, en el Capítulo 9, para representar la velocidad angular de una partícula que se mueve en círculo (o, más generalmente, de cualquier objeto giratorio). ¿Por qué volver a mencionarlo ahora con un propósito aparentemente completamente diferente?
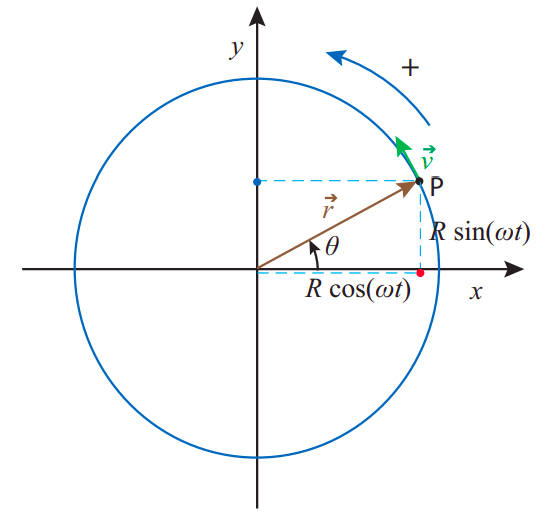
La respuesta es que existe una relación muy estrecha entre el movimiento armónico simple y el movimiento circular con velocidad constante, como\(\PageIndex{2}\) ilustra la Figura: a medida que el punto P gira con velocidad angular constante\(\omega\), su proyección sobre el\(x\) eje (el punto rojo en la figura) se realiza simple movimiento armónico con frecuencia angular\(\omega\) (y amplitud\(R\)). (Por supuesto, no hay nada especial en el\(x\) eje; la proyección sobre cualquier otro eje también realizará un movimiento armónico simple con la misma frecuencia angular; por ejemplo, el punto azul en la figura).
Si la velocidad angular de la partícula en la Figura\(\PageIndex{2}\) es constante, entonces su “período orbital” (el tiempo necesario para completar una revolución) será\(T = 2\pi/\omega\), y este también será el período del movimiento armónico asociado (el tiempo que tarda el movimiento en repetirse). Puedes ver esto directamente desde la Ecuación (\ ref {eq:11.3}): si aumentas el tiempo\(t\) por\(2\pi/\omega\), obtienes el mismo valor de\(x\):
\[ x\left(t+\frac{2 \pi}{\omega}\right)=A \cos \left[\omega\left(t+\frac{2 \pi}{\omega}\right)\right]=A \cos (\omega t+2 \pi)=A \cos (\omega t)=x(t) \label{eq:11.5} .\]
Dado que la frecuencia\(f\) de un oscilador es igual a 1/\(T\), esto nos da la siguiente relación entre\(f\) y\(\omega\):
\[ f=\frac{1}{T}=\frac{\omega}{2 \pi} \label{eq:11.6} .\]
Una manera de saber si se está hablando de la frecuencia de un oscilador (\(f\)) o de su frecuencia angular (\(\omega\)) —aparte de los diferentes símbolos, por supuesto— es prestar atención a las unidades. La frecuencia\(f\) suele darse en hercios, mientras que la frecuencia angular siempre\(\omega\) se da en radianes por segundo. Aparte del factor de\(2\pi\), son, por supuesto, completamente equivalentes; a veces uno es simplemente más conveniente que el otro. Por otro lado, la única manera de saber si\(\omega\) es la frecuencia angular de un oscilador armónico o la velocidad angular de algo que se mueve en círculo es desde el contexto. (En este capítulo, por supuesto, siempre será el primero).
Volvamos ahora a la Ecuación\ ref {eq:11.3} para nuestro sistema bloque-on-a-spring. La derivada con respecto al tiempo nos dará la velocidad del bloque. Esta es una simple aplicación de la regla de la cadena del cálculo:
\[ v(t)=\frac{d x}{d t}=-\omega A \sin (\omega t) \label{eq:11.7} .\]
Otra derivada nos dará entonces la aceleración:
\[ a(t)=\frac{d v}{d t}=-\omega^{2} A \cos (\omega t) \label{eq:11.8} .\]
Tenga en cuenta que la aceleración siempre es proporcional a la posición, solo con el signo opuesto. La constante de proporcionalidad es\(\omega^2\). Dado que la fuerza ejercida por el resorte sobre el bloque es\(F = −kx\) (porque estamos midiendo la posición desde la posición de equilibrio\(x_0\)), la segunda ley de Newton,\(F = ma\), nos da
\[ ma = -kx \label{eq:11.9} \]
y puedes comprobar por ti mismo que esto quedará satisfecho si\(x\) viene dado por la Ecuación (\ ref {eq:11.3}),\(a\) está dado por la Ecuación (\ ref {eq:11.8}), y\(\omega\) está dado por Ecuación (\ ref {eq:11.4}).
La expresión (\ ref {eq:11.4}) for\(\omega\) es típica de lo que encontramos para muchos tipos diferentes de osciladores: la fuerza restauradora (aquí representada por la constante elástica\(k\)) y la inercia del objeto (\(m\)) juntos determinan la frecuencia del movimiento, actuando en direcciones opuestas: a mayor fuerza de restauración significa una frecuencia más alta (oscilaciones más rápidas) mientras que una inercia mayor significa una frecuencia más baja (oscilaciones más lentas, una respuesta más “lenta”).
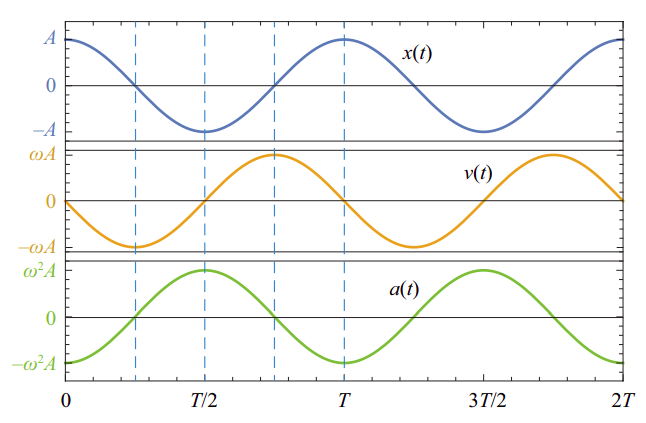
Las gráficas de posición, velocidad y aceleración para el movimiento (\ ref {eq:11.3}) se muestran en la Figura\(\PageIndex{3}\) siguiente. Es posible que desee prestar atención a algunas de sus características principales. Por ejemplo, la posición y la velocidad son lo que llamamos “90\(^{\circ}\) fuera de fase”: uno es máximo (o mínimo) cuando el otro es cero. La aceleración, en cambio, es “180\(^{\circ}\) fuera de fase” (es decir, en completa oposición) con la posición. Como resultado de eso, todas las combinaciones de signos para\(a\) y\(v\) son posibles: el objeto puede estar moviéndose hacia la derecha con aceleración positiva o negativa (dependiendo de qué lado del origen se encuentre), y de igual manera cuando se mueve hacia la izquierda.
Dado que el tiempo que elegimos como\(t\) = 0 es arbitrario, la función en Ecuación (\ ref {eq:11.3}) (que asume que\(t\) = 0 es cuando el desplazamiento del objeto es máximo y positivo) claramente no es la fórmula más general para el movimiento armónico simple. Otra forma de ver esto es darnos cuenta de que podríamos haber iniciado la moción de manera diferente. Por ejemplo, podríamos haber golpeado el bloque con una fuerza aguda, “impulsiva”, durando muy poco tiempo, por lo que habría adquirido una velocidad sustancial antes de que pudiera haberse movido muy lejos de su posición inicial (equilibrio). En tal caso, el movimiento sería mejor descrito por una función sinusoidal, tal como\(x(t) = A \sin(\omega t)\), que es cero a\(t\) = 0 pero cuya derivada (la velocidad del objeto) es máxima en ese momento.
Si nos ceñimos a usar cosenos, por definición, entonces la ecuación más general para la posición de un oscilador armónico simple es la siguiente:
\[ x(t)=A \cos (\omega t+\phi) \label{eq:11.10} \]
donde\(\phi\) es lo que llamamos un “ángulo de fase”, que nos permite hacer coincidir la función con las condiciones iniciales, con lo que quiero decir, la posición inicial y la velocidad del objeto. Específicamente, se puede ver, ajustando\(t\) = 0 en Ecuación (\ ref {eq:11.10}) y su derivada, que la posición inicial y velocidad del movimiento descrito por la Ecuación (\ ref {eq:11.10}) son
\ begin {align}
x_ {i} &=A\ cos\ phi\ nonumber\\
v_ {i} &=-\ omega A\ sin\ phi\ label {eq:11.11}.
\ end {align}
Por el contrario, si te dan\(x_i\) y\(v_i\), puedes usar Eqs. (\ ref {eq:11.11}) para determinar\(A\) y\(\phi\), que es lo que necesitas saber para poder usar la Ecuación (\ ref {eq:11.10}) (tenga en cuenta que la frecuencia angular\(\omega\),, no depende de las condiciones iniciales, siempre es la misma independientemente de cómo elijas iniciar el movimiento). Específicamente, se puede verificar que las Eqs. (\ ref {eq:11.11}) implican lo siguiente:
\[ A^{2}=x_{i}^{2}+\frac{v_{i}^{2}}{\omega^{2}} \label{eq:11.12} \]
y luego, una vez que lo sepas\(A\), puedes obtener\(\phi\) de cualquiera\(x_i = A \cos \phi\) o\(v_i = −\omega A \sin \phi\) (de hecho, ya que el seno inverso y el coseno inverso son funciones multivalores, debes usar ambas ecuaciones, para asegurarte de obtener el signo correcto para\(\phi\)).
Energía en Movimiento Armónico Simple
La ecuación (\ ref {eq:11.11}) anterior en realidad se deriva del principio de conservación de energía para un oscilador armónico. Considera nuevamente la masa en el resorte en la Figura\(\PageIndex{2}\). Su energía cinética es claramente\(K = \frac{1}{2}mv^2\), mientras que la energía potencial en la primavera lo es\(\frac{1}{2}kx^2\). Usando la ecuación (\ ref {eq:11.10}) y su derivada, tenemos
\ begin {align}
U^ {s p r} &=\ frac {1} {2} k A^ {2}\ cos ^ {2} (\ omega t+\ phi)\ nonumber\\
K &=\ frac {1} {2} m\ omega^ {2} A^ {2}\ sin ^ {2} (\ omega t+\ phi)\ etiqueta {eq:11.13}.
\ end {align}
Recordando la Ecuación (\ ref {eq:11.4}), tenga en cuenta que\(\omega^2 = k/m\), así que si sustituye esto en la segunda ecuación anterior, puede ver que la amplitud tanto del potencial como de la energía cinética es la misma, es decir,\(\frac{1}{2}kA^2\). Ya que, para cualquier ángulo\(\theta\), siempre es cierto que\(\cos^2 \theta + \sin^2 \theta = 1\), encontramos
\[ E_{s y s}=U^{s p r}+K=\frac{1}{2} k A^{2}=\frac{1}{2} m \omega^{2} A^{2} \label{eq:11.14} \]
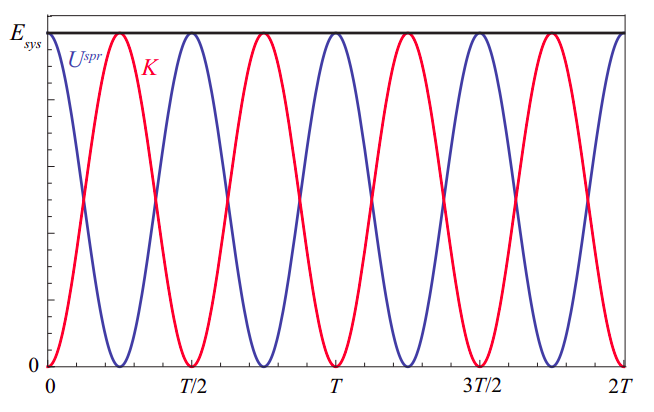
por lo que la energía total del sistema es constante (independiente del tiempo), en ello debería ser, en ausencia de disipación. La figura\(\PageIndex{4}\) muestra cómo las energías potenciales y cinéticas oscilan en oposición, por lo que una es máxima siempre que la otra es mínima. También muestra que oscilan dos veces más rápido que el propio oscilador: por ejemplo, la energía potencial es máxima tanto cuando el desplazamiento es máximo (resorte estirado al máximo) como cuando es mínimo (resorte comprimido al máximo). De igual manera, la energía cinética es máxima cuando el oscilador pasa por la posición de equilibrio, independientemente de si se mueve hacia la izquierda o hacia la derecha.
Oscilador armónico sujeto a una fuerza externa constante
Considera una masa que cuelga de un resorte ideal suspendido del techo, como en la Figura\(\PageIndex{5}\) a continuación (página siguiente). Se supone que la longitud relajada del resorte es\(l\) tal que, en ausencia de gravedad, la posición de equilibrio del objeto estaría a la altura que\(y_0\) se muestra en la figura\(\PageIndex{5}\) (a). En presencia de gravedad, por supuesto, el resorte necesita estirarse, para equilibrar el peso del objeto, y así la posición de equilibrio real para el sistema será\(y^{\prime}_0\), como se muestra en la figura\(\PageIndex{5}\) (b). La fuerza hacia arriba desde el muelle en ese punto será\(-k\left(y_{0}^{\prime}-y_{0}\right)\), y para equilibrar la gravedad debemos tener
\[ -k\left(y_{0}^{\prime}-y_{0}\right)-m g=0 \label{eq:11.15} .\]
Supongamos que ahora estiramos el resorte más allá de esta nueva posición de equilibrio, por lo que la masa está ahora a una altura\(y\)\(\PageIndex{5}\) (figura (c)). ¿Qué pasa entonces? La fuerza neta hacia arriba será\(-k\left(y-y_{0}\right)-m g\), pero usando la ecuación (\ ref {eq:11.15}) esto se puede reescribir como
\[ F_{n e t}=-k\left(y-y_{0}\right)-m g=-k\left(y-y_{0}^{\prime}\right)--k\left(y_{0}^{\prime}-y_{0}\right)-m g=-k\left(y-y_{0}^{\prime}\right) \label{eq:11.16} .\]
Este es un resultado notable, porque la fuerza de la gravedad ha desaparecido por completo de la expresión final. Básicamente, el sistema se comporta como si consistiera solo en un resorte de constante\(k\) con longitud de equilibrio\(l^{\prime}=l+y_{0}-y_{0}^{\prime}\), y sin gravedad. En otras palabras, lo único que hace la gravedad es cambiar la posición de equilibrio, de modo que si ahora desplazas la masa, oscilará alrededor\(y_{0}^{\prime}\) en lugar de alrededor\(y_0\). El período y frecuencia de la oscilación son los mismos que si el resorte fuera horizontal.
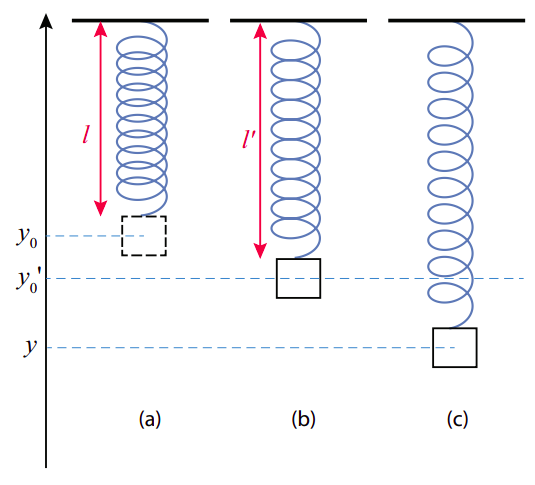
Si bien lo he establecido aquí para el caso específico donde el oscilador involucra un resorte, y la fuerza externa es la gravedad, este es un resultado completamente general, válido para cualquier oscilador armónico simple, ya que para tal sistema la fuerza restauradora siempre será una función lineal del desplazamiento ( que es todo lo que se requiere para que las matemáticas funcionen). Mientras la fuerza externa sea constante, la frecuencia de las oscilaciones no se verá afectada, y solo cambiará la posición de equilibrio. En un ejemplo al final del capítulo (bajo “Temas Avanzados”) te mostraré cómo puedes hacer uso de esto para calcular el efecto de fricción en la combinación masa-resorte horizontal en la Figura\(\PageIndex{1}\).
Una cosa que hay que tener en cuenta, sin embargo, es que cuando el oscilador es sometido a una fuerza externa, como fue el caso aquí, su energía no se mantendrá, en general, constante (a diferencia de lo que vimos en la subsección anterior “Energía en Movimiento Armónico Simple”), ya que la fuerza externa será haciendo trabajo en el sistema a medida que oscila. Si la fuerza externa es constante, y no cambia de dirección, este trabajo será positivo la mitad del tiempo, y negativo la mitad del tiempo. Si es fricción cinética, entonces por supuesto cambiará de dirección cada medio ciclo, y el trabajo será negativo todo el tiempo.
En el caso mostrado en la Figura\(\PageIndex{5}\), la fuerza externa es la gravedad, que sabemos que es una fuerza conservadora, por lo que la energía que se conservará será la energía total del sistema que incluye la oscilación y la Tierra, y de ahí también la energía potencial gravitacional (para lo cual podemos utilizar aquí la forma familiar\(U^G = mgy\)):
\[ E_{\text {osc+earth }}=U^{s p r}+K+U^{G}=\frac{1}{2}\left(y-y_{0}\right)^{2}+\frac{1}{2} m v^{2}+m g y=\text { const } \label{eq:11.17} .\]
La razón por la que ya no es posible combinar los términos\(U^{spr} + K\) en la constante\(\frac{1}{2} kA^2\), como en la Ecuación (\ ref {eq:11.14}), es que ahora tenemos
\ begin {align}
&y (t) =y_ {0} ^ {\ prime} +A\ cos (\ omega t+\ phi)\ nonumber\\
&v (t) =-\ omega A\ sin (\ omega t+\ phi)\ label {eq:11.18}
\ end {align}
por lo que las oscilaciones se centran alrededor de la nueva posición de equilibrio\(y_{0}^{\prime}\), pero la energía del resorte no es cero en ese punto: es cero en\(y = y_0\) su lugar. Puedes comprobar por ti mismo, sin embargo, que si sustitues Eqs. (\ ref {eq:11.18}) en Ecuación (\ ref {eq:11.17}), y hacer uso del hecho de que\(k\left(y_{0}^{\prime}-y_{0}\right)=-m g\) (Ecuación (\ ref {eq:11.15}), efectivamente obtienes una constante, como deberías.


