11.3: Péndulos
- Page ID
- 128040
El péndulo simple
Además de las masas en resortes, los péndulos son otro ejemplo de un sistema que exhibirá un movimiento armónico simple, al menos aproximadamente, siempre que la amplitud de las oscilaciones sea pequeña. El péndulo simple es solo una masa (o “bob”), aproximada aquí como una partícula puntual, suspendida de una cuerda sin masa, inextensible, como en la Figura\(\PageIndex{1}\).
Podríamos analizar el movimiento del bob usando los métodos generales introducidos en el Capítulo 8 para tratar el movimiento en dos dimensiones —descomponer todas las fuerzas en componentes y aplicarlas\(\vec{F}_{net} = m\vec{a}\) a lo largo de dos direcciones ortogonales— pero esto resulta complicado por el hecho de que tanto la dirección del movimiento y la dirección de la aceleración están cambiando constantemente. Si bien, bajo el supuesto de pequeñas oscilaciones, resulta que el simple uso de las direcciones vertical y horizontal es lo suficientemente bueno, esto no es inmediatamente obvio, y posiblemente no es la forma más pedagógica de proceder.
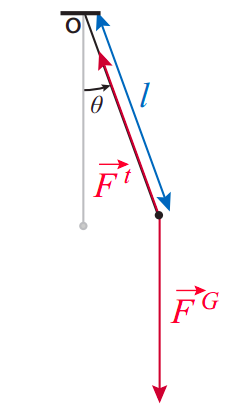
En cambio, voy a aprovechar el hecho obvio de que el bob se mueve en un arco de círculo, y que ya hemos desarrollado en el Capítulo 9 todo un conjunto de herramientas para hacer frente a ese tipo de movimiento. Por lo tanto, describamos la posición del péndulo por el ángulo que hace con la vertical\(\theta\), y dejar que\(\alpha = d^2 \theta /dt^2\) sea la aceleración angular; entonces podemos escribir la ecuación del movimiento en la forma\(\tau_{net} = I\alpha\), con los pares tomados alrededor del centro de rotación, es decir, el punto de que el péndulo está suspendido. Entonces el par debido a la tensión en la cuerda es cero (ya que su línea de acción pasa por el centro de rotación), y\(\tau_{net}\) es solo el par debido a la gravedad, que se puede escribir
\[ \tau_{n e t}=-m g l \sin \theta \label{eq:11.19} .\]
El signo menos está ahí para hacer cumplir una convención de signo consistente para\(\theta\) y\(\tau\): si, por ejemplo, elijo en sentido antihorario como positivo para ambos, entonces observo que cuando\(\theta\) es positivo (péndulo a la derecha de la vertical),\(\tau\) es en sentido horario, y por lo tanto negativo, y viceversa. Esto es característico de un par restaurador, es decir, uno que siempre intentará empujar el sistema de nuevo a su posición de equilibrio (la vertical en este caso).
En cuanto al momento de inercia del bob, es justo\(I = ml^2\) (si lo tratamos como solo una partícula puntual), entonces la ecuación\(\tau_{net} = I\alpha\) toma la forma
\[ m l^{2} \frac{d^{2} \theta}{d t^{2}}=-m g l \sin \theta \label{eq:11.20} .\]
La masa y un factor de\(l\) cancelación, y obtenemos
\[ \frac{d^{2} \theta}{d t^{2}}=-\frac{g}{l} \sin \theta \label{eq:11.21} .\]
La ecuación (\ ref {eq:11.21}) es un ejemplo de lo que se conoce como ecuación diferencial. El problema es encontrar una función del tiempo,\(\theta (t)\), que satisfaga esta ecuación; es decir, cuando tomas su segunda derivada el resultado es igual a\(−(g/l) \sin[\theta (t)]\). Tales funciones existen y se llaman funciones elípticas; están incluidas en muchos paquetes matemáticos modernos, pero aún no son fáciles de usar. Más importante aún, las oscilaciones que describen, en general, no son del tipo armónico simple.
Por otro lado, si la amplitud de las oscilaciones es pequeña, de manera que el ángulo\(\theta\), expresado en radianes, es un número pequeño, podemos hacer una aproximación que simplifique enormemente el problema, es decir,
\[ \sin \theta \simeq \theta \label{eq:11.22} .\]
Esto se conoce como la aproximación de ángulo pequeño, y requiere\(\theta\) estar en radianes. Como ejemplo, si\(\theta\) = 0.2 rad (que corresponde a aproximadamente 11.5\(^{\circ}\)), encontramos\(\sin \theta\) = 0.199, a una precisión de tres cifras.
Con esta aproximación, la ecuación a resolver se vuelve mucho más sencilla:
\[ \frac{d^{2} \theta}{d t^{2}}=-\frac{g}{l} \theta \label{eq:11.23} .\]
De hecho, ya hemos resuelto una ecuación completamente equivalente a esta del apartado anterior: esa era la ecuación (11.2.8) para el sistema masa-en-resorte, que puede reescribirse como
\[ \frac{d^{2} x}{d t^{2}}=-\frac{k}{m} x \label{eq:11.24} \]
ya que\(a = d^2x/dt^2\). Al igual que las soluciones a (\ ref {eq:11.24}) podrían escribirse en la forma\(x(t) = A \cos(\omega t + \phi)\), con\(\omega=\sqrt{k / l}\), las soluciones a (\ ref {eq:11.23}) se pueden escribir como
\ begin {align}
\ theta (t) &=A\ cos (\ omega t+\ phi)\ nonumber\
\ omega &=\ sqrt {\ frac {g} {l}}\ label {eq:11.25}.
\ end {align}
Esto nos dice que si un péndulo no se aleja demasiado de la vertical (digamos, alrededor de 10\(^{\circ}\) o menos) realizará oscilaciones armónicas simples aproximadas, con un periodo de
\[ T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{l}{g}} \label{eq:11.26} .\]
Esto depende sólo de la longitud del péndulo, y permanece constante aun cuando las oscilaciones se van apagando, razón por la cual se convirtió en la base de los dispositivos cronometradores, comenzando con la invención del reloj de péndulo por Christiaan Huygens en 1656. En particular, un péndulo de longitud\(l\) = 1 m tendrá un periodo de casi exactamente 2 s, que es lo que te da el conocido ritmo de “tic-tac” de un “reloj de abuelo”, una vez por segundo (es decir, una vez cada medio periodo).
El “Péndulo Físico”
Por un “péndulo físico” se entiende típicamente cualquier dispositivo similar a un péndulo para el cual el momento de inercia no viene dado por la simple expresión\(I = ml^2\). Esto significa que la masa no se concentra en una sola partícula parecida a un punto a una\(l\) distancia del punto de suspensión; más bien, por ejemplo, el bob podría tener un tamaño que no es despreciable en comparación con\(l\) (como en la Figura 11.1.1), o la “cuerda” podría tener una masa sustancial por sí mismo, podría ser, por ejemplo, una cadena, como en el columpio de un patio de recreo, o una varilla de metal, como en la mayoría de los relojes de péndulo.
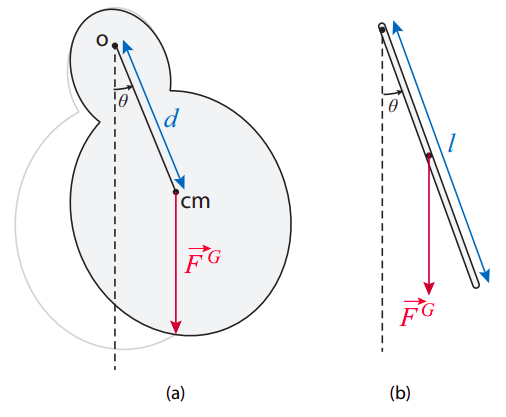
Independientemente de la razón, tener que lidiar con una masa distribuida significa también que se necesita usar el centro de masa del sistema como punto de aplicación de la fuerza de gravedad. Cuando se hace esto, el movimiento del péndulo puede describirse nuevamente por el ángulo entre la vertical y una línea que conecta el punto de suspensión y el centro de masa. Si la distancia entre estos dos puntos es\(d\), entonces el par debido a la gravedad es\(−mgd \sin \theta\), y la única otra fuerza en el sistema, la fuerza en el punto de pivote, no ejerce torque alrededor de ese punto, por lo que podemos escribir la ecuación de movimiento en la forma
\[ I \frac{d^{2} \theta}{d t^{2}}=-m g d \sin \theta \label{eq:11.27} .\]
Bajo la aproximación de ángulo pequeño, esto conducirá nuevamente a un simple movimiento armónico, solo que ahora con una frecuencia angular dada por
\[ \omega=\sqrt{\frac{m g d}{I}} \label{eq:11.28} .\]
Como ejemplo, considere las oscilaciones de una varilla uniforme y delgada de longitud\(l\) y masa\(m\) pivotada en un extremo. Entonces tenemos\(I = ml^{2}/3\), y\(d = l/2\), así Ecuación (\ ref {eq:11.28}) da
\[ \omega=\sqrt{\frac{3 g}{2 l}} \label{eq:11.29} .\]
Esto es aproximadamente 22% más grande que el resultado (\ ref {eq:11.25}) para un péndulo simple de la misma longitud, lo que implica un período correspondientemente más corto.


