11.5: Ejemplos

Ejemplo\(\PageIndex{1}\): Oscillator in a box (a basic accelerometer!)

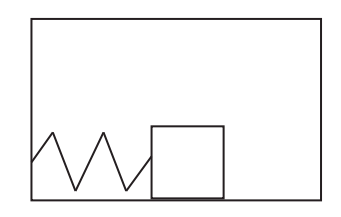
Considera un sistema bloque-resorte dentro de una caja, como se muestra en la figura. El bloque está unido al resorte, el cual está unido a la pared interior de la caja. La masa del bloque es de 0.2 kg. Para las partes (a) a (f), supongamos que la caja no se mueve.

Supongamos que tira del bloque 10 cm hacia la derecha y lo sueltas. La frecuencia angular de las oscilaciones es de 30 rad/s, descuida la fricción entre el bloque y el fondo de la caja.

1. ¿Cuál es la constante de primavera?
2. ¿Cuál será la amplitud de las oscilaciones?
3. Tomando a la derecha para ser positivo, ¿en qué punto de la oscilación es la velocidad mínima y cuál es su valor mínimo?
4. ¿En qué punto de la oscilación es la aceleración mínima, y cuál es su valor mínimo?
5. ¿Cuál es la energía total del sistema de muelles?
6. Si tomas\(t\) = 0 para ser el instante en que sueltas el bloque, escribe una ecuación de movimiento para la oscilación,\(x(t)\) =? , identificando los valores de todas las constantes que utilices.
7. Imagínese ahora que la caja, con el resorte y el bloque en ella, comienza a moverse hacia la izquierda con una aceleración\(a\) = −4 m/s ². ¿Por cuánto se desplaza la posición de equilibrio del bloque (relativa a la caja) y en qué dirección?

Solución

La mayor parte de esto es realmente bastante sencillo, ya que es solo cuestión de usar correctamente las ecuaciones introducidas en este capítulo:

(a) Ya que sabemos que para este tipo de situaciones, la frecuencia angular, la masa y la constante elástica están relacionadas por

\[ \omega=\sqrt{\frac{k}{m}} \nonumber \]

resolvemos esto para\(k\):

\[ k=m \omega^{2}=0.2 \: \mathrm{kg} \times\left(30 \: \frac{\mathrm{rad}}{\mathrm{s}}\right)^{2}=180 \: \frac{\mathrm{N}}{\mathrm{m}} \nonumber \]

(b) La amplitud será de 10 cm, ya que se libera en ese punto sin energía cinética.

(c) La velocidad es mínima (mayor en magnitud, pero con signo negativo) a medida que el objeto pasa por la posición de equilibrio moviéndose hacia la izquierda.

\[ v_{\min }=-\omega A=-\left(30 \: \frac{\mathrm{rad}}{\mathrm{s}}\right) \times 0.1 \: \mathrm{m}=-3 \: \frac{\mathrm{m}}{\mathrm{s}} \nonumber \]

(d) La aceleración es mínima (nuevamente, mayor en magnitud, pero con signo negativo) cuando el resorte se estira al máximo (el bloque está más alejado a la derecha), ya que esto le da la fuerza máxima en la dirección negativa:

\[ a_{\min }=-\omega^{2} A=-\left(30 \: \frac{\mathrm{rad}}{\mathrm{s}}\right)^{2} \times 0.1 \: m=-90 \: \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber \]

e) La energía total viene dada por la fórmula (cualquiera de ellas es aceptable)

\[ E=\frac{1}{2} m \omega^{2} A^{2}=\frac{1}{2} k A^{2}=\frac{1}{2}(180 \: \mathrm{N} / \mathrm{m}) \times(0.1 \: \mathrm{m})^{2}=0.9 \: \mathrm{J} \nonumber \]

(También podrías usar\(E = \frac{1}{2}mv^{2}_{max}\).)

f) El resultado es

\[ x(t)=A \cos (\omega t)=A \sin \left(\omega t+\frac{\pi}{2}\right) \nonumber \]

con\(A\) = 0.1 m y\(\omega\) = 30 rad/s También podrías simplemente escribir los números directamente en la fórmula, pero en ese caso necesitas incluir las unidades implícita o explícitamente. Lo que quiero decir con “implícitamente” es decir algo como: “\(x(t)=0.1 \cos(30t)\), con\(x\) en metros y\(t\) en segundos”.

(g) La posición de equilibrio es donde el bloque podría sentarse en reposo en relación con la caja. En ese caso, con relación al suelo fuera de la caja, se estaría moviendo con una aceleración\(a\) = -4 m/s ², y la fuerza del resorte (que es la única fuerza real que actúa sobre el bloque) tendría que proporcionar esta aceleración:

\[ F_{x}^{s p r}=-k \Delta x=m a \nonumber \]

por lo

\[ \Delta x=-\frac{m a}{k}=\frac{0.2 \: k g \times 4 \: m / s^{2}}{180 \: N / m}=0.00444 \: m \nonumber \]

o 4.44 mm. Esto es positivo, por lo que el resorte se estira, la posición de equilibrio del bloque se desplaza hacia la derecha, en relación con las paredes de la caja.

Otra forma de ver esto es la siguiente. Como vimos en el capítulo anterior (sección 10.2), un sistema de referencia acelerado, con aceleración a, aparece “desde el interior” como un sistema de referencia inercial sujeto a una interacción gravitacional que tira de cualquier objeto con masa\(m\) con una fuerza igual a\(ma\) en la dirección frente a la aceleración. Por lo tanto, dentro de la caja, que se está acelerando hacia la izquierda, el bloque se comporta como si hubiera una fuerza de gravedad de magnitud\(ma\), tirando de él hacia la derecha. Es decir, tenemos una situación como la ilustrada en la Figura 11.2.5, sólo de lado. Como en ese caso, encontramos que la posición de equilibrio se desplaza lo suficiente para que la fuerza del resorte estirado coincida con la “fuerza de la gravedad”, y de esta manera obtenemos nuevamente la ecuación\(F^{spr}_{x} = ma\).

Para obtener un acelerómetro, proporcionamos a la caja algún mecanismo de lectura que nos puede indicar el cambio en la posición de equilibrio del oscilador. Este principio básico es una de las formas en que funcionan los acelerómetros, y los llamados “sistemas de navegación inercial”.

Ejemplo\(\PageIndex{2}\): Meter stick as a physical pendulum

Al trabajar en el laboratorio en pares, notas que un palo medidor suspendido del medio se comporta un poco como un péndulo, en que realiza oscilaciones muy lentas al inclinarlo ligeramente. Intrigado, notas que está suspendido por un simple lazo de cuerda atado en un nudo en la parte superior (ver figura). Se mide el periodo de las oscilaciones para que sea de aproximadamente 5 s, y el ancho del palo para que sea de aproximadamente 2.5 cm.

1. ¿Qué te dice esto sobre la cantidad\(I/M\), dónde\(M\) está la masa del palo, y\(I\) su momento de inercia alrededor de cierto punto?
2. ¿Cuál es el “cierto punto” mencionado en la letra a)?

Solución

Como muestra la imagen de abajo, el palo se comportará como un péndulo físico, oscilando alrededor del punto de suspensión O, que en este caso está justo al lado del palo, donde está el nudo. Como se ve en el detalle de soplado, si el ancho del palo es w, el centro de masa del palo se ubica a una\(d = w/2\) distancia del punto de suspensión:

Como se muestra en la Sección 11.3, tenemos entonces

\[ \omega=\sqrt{\frac{M g w}{2 I}} \label{eq:11.30} .\]

Al cuadrar esto, y resolver para\(I/M\),

\[ \frac{I}{M}=\frac{g w}{2 \omega^{2}}=\frac{9.8 \: \mathrm{m} / \mathrm{s}^{2} \times 0.025 \: \mathrm{m}}{2 \times(2 \pi / 5 \: \mathrm{s})^{2}}=0.0776 \: \mathrm{m}^{2} \label{eq:11.31} .\]

El momento de inercia se va a calcular alrededor del punto O, es decir, el punto de suspensión (donde está el nudo en la figura). Como referencia, el momento de inercia de una varilla delgada de longitud\(l\) alrededor de su punto medio es\(Ml^2/12 = 0.083l^2\). La longitud del bastón medidor es, por supuesto, de 1 m, por lo que el resultado\(I/M\) ∼ 0.08 m ² obtenido arriba parece razonable.