11.6: Temas avanzados

Masa en un muelle amortiguado por fricción con una superficie

Considere el sistema representado en la Figura 11.2.1 en presencia de fricción entre el bloque y la superficie. Que el coeficiente de fricción cinética sea\(\mu_k\) y el coeficiente de fricción estática sea\(\mu_s\). Como es habitual, vamos a suponer eso\(\mu_s \geq \mu_k\).

A medida que la masa oscila, experimentará una fuerza de fricción cinética de magnitud\(F^k = \mu_k mg\), en la dirección opuesta a la dirección del movimiento; es decir, una fuerza que cambia de dirección cada medio período. Como se muestra en la sección 11.2, esta fuerza no cambia la frecuencia del movimiento, sino que desplaza la posición de equilibrio en la dirección de la fuerza, es decir, más cerca del punto de partida para cada media oscilación. Como resultado de ello, la amplitud para cada media oscilación se reduce con respecto a la anterior.

Deje que la posición de equilibrio original (en ausencia de fricción) sea\(x_0\) = 0. Supongamos que desplazamos la masa una distancia\(A\) a la derecha (llamar a esta posición, el punto de partida para el primer medio-swing,\(x_1 = A\)), y soltamos. En presencia de fricción, la posición de equilibrio para esta primera media oscilación se convierte en el punto\(x_{0}^{\prime}=F^{k} / k=\mu_{k} m g\), por lo que la amplitud real de esta primera media oscilación será\(A_{1}=x_{1}-x_{0}^{\prime}=A-x_{0}^{\prime}\), y el movimiento resultante será

\[ \left.x(t)=x_{0}^{\prime}+A_{1} \cos (\omega t) \quad \text { (first half-period, } 0 \leq t \leq \pi / \omega\right) \label{eq:11.32} .\]

Continuando con el proceso, vemos que\(A_{1}=A-x_{0}^{\prime}\),\(A_{2}=A-3 x_{0}^{\prime}\),\(A_{3}=A-5 x_{0}^{\prime} \ldots A_{n}=A-(2 n-1) x_{0}^{\prime}\). Por supuesto, esto no puede continuar para siempre, ya que requerimos que la amplitud sea una cantidad positiva; por lo que el movimiento consistirá sólo en\(n\) medio periodos, donde\(n\) es un entero tal que\(A-(2 n-1) x_{0}^{\prime}>0\) pero\(A-(2 n+1) x_{0}^{\prime}<0\). (Es decir,\(n\) es igual a la parte entera de\(\left.\left(A / x_{0}^{\prime}+1\right) / 2 .\right)\).)

En la figura se muestra un ejemplo de cómo iría esto, para la siguiente elección de parámetros: periodo\(T\) = 1 s,\(\mu_k\) = 0.1, y\(A\) = 0.18 m. Obsérvese que, dado que\(x_{0}^{\prime}\) depende únicamente de la relación\(m/k = 1/ \omega^2\), no hay necesidad de especificar\(m\) y\(k\) por separado. Obtenemos\(\omega = 2\pi /T = 2\pi\) rad/s,\(x_{0}^{\prime} = \mu_k g/ \omega^2\) = 0.0248 m, y\(\left(A / x_{0}^{\prime}+1\right) / 2=4.13\), lo que significa que el movimiento se prolongará por 4 medios periodos antes de detenerse.

Figura\(\PageIndex{1}\): Oscilaciones amortiguadas.

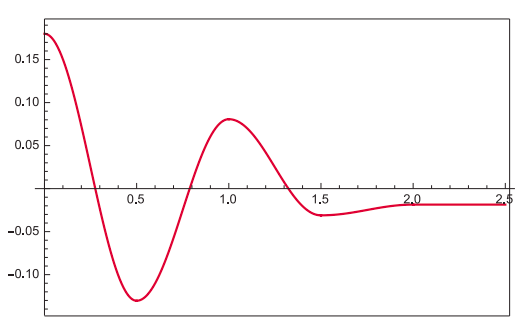
Obsérvese que, en general, el oscilador no se detiene en la posición de equilibrio. Más bien, su posición final será al final del último medio swing, que es o bien\(x_{0}^{\prime}-A_{n}\) (si el número\(n\) de semiperiodos es impar), o bien\(-x_{0}^{\prime}+A_{n}\), si el número\(n\) es par. De cualquier manera, en ese punto el resorte estará ejerciendo una fuerza de magnitud

\[ F^{s p r}=k\left|x_{0}^{\prime}-A_{n}\right|=k\left|x_{0}^{\prime}-A+(2 n-1) x_{0}^{\prime}\right|=k\left|A-2 n x_{0}^{\prime}\right|<k x_{0}^{\prime}=F^{k} \label{eq:11.34} .\]

Ya que esperamos que la fuerza de fricción estática,\(F^s\), sea mayor que\(F^k\), esto nos dice que en este punto el resorte no está ejerciendo la fuerza suficiente para conseguir que la masa vuelva a moverse.

Nota: Solo para que conste, esta no es la manera en que se suele manejar la disipación en movimiento armónico simple. Lo convencional es asumir una fuerza de amortiguación que sea proporcional a la velocidad del oscilador. Es casi seguro que verá este enfoque más estándar (que conduce a una ecuación diferencial relativamente simple) en algún curso posterior.

El experimento Cavendish: cómo medir\(G\) con una balanza de torsión

Supongamos que quieres intentar duplicar el experimento de Cavendish para medir directamente la fuerza gravitacional entre dos masas (y por lo tanto, indirectamente, el valor de\(G\)). Tomas dos objetos relativamente pequeños e idénticos, cada uno de masa\(m\), y los unes a los extremos de una varilla de longitud\(l\) (digamos que la masa de la varilla es insignificante, por simplicidad), haciendo una especie de mancuerna; luego suspendes esto del techo, por el punto medio, usando una línea de nylon.

Figura\(\PageIndex{2}\):: (a) Balanza de torsión. Los extremos de la oscilación se dibujan en negro y gris, respectivamente. b) La vista desde arriba. La línea discontinua indica la posición de equilibrio. (c) Ante la presencia de dos grandes masas cercanas, la posición de equilibrio se inclina muy ligeramente; las líneas azul claro en el fondo muestran la oscilación en ausencia de las masas, para referencia.

Ahora has hecho una balanza de torsión similar a la que usó Cavendish. Probablemente descubrirás que es muy difícil mantenerlo inmóvil: el más mínimo desplazamiento hace que oscile alrededor de una posición de equilibrio. La forma en que funciona es que un desplazamiento angular\(\theta\) desde el equilibrio pone un pequeño giro en la línea, lo que resulta en un par de restauración\(\tau = −\kappa \theta\), donde\(\kappa\) está la constante de torsión para su configuración. Si tu mancuerna tiene momento de inercia\(I\), entonces la ecuación de movimiento te\(\tau = I \alpha\) da

\[I \frac{d^{2} \theta}{d t^{2}}=-\kappa \theta \label{eq:11.35} .\]

Si compara esto con la Ecuación (11.3.3), y sigue la derivación allí, puede ver que el período de oscilación es

\[ T=2 \pi \sqrt{\frac{I}{\kappa}} \label{eq:11.36} \]

así que si mides\(T\) puedes conseguir\(\kappa\), ya que\(I = 2m(l/2)^2 = ml^2/2\) para la mancuerna.

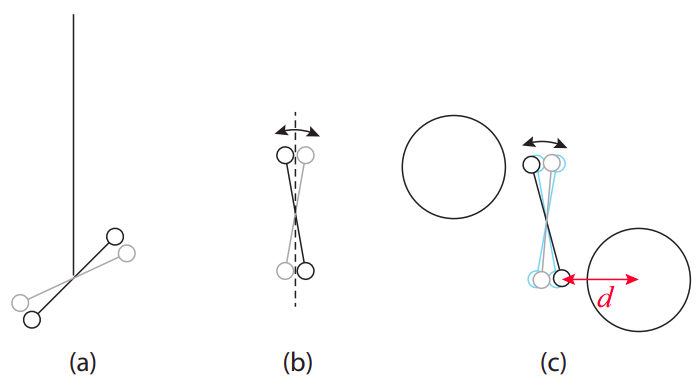
Ahora suponga que trae dos masas grandes, una distancia\(d\) cada una de cada extremo de la mancuerna, perpendiculares al eje de la mancuerna, y una a cada lado, como en la figura. La fuerza gravitacional\(F^G = GmM/d^2\) entre la masa grande y pequeña da como resultado un par neto “externo” de magnitud

\[ \tau_{e x t}=2 F^{G} \times \frac{l}{2}=F^{G} l \label{eq:11.37} .\]

Este par provocará un desplazamiento muy pequeño, tan pequeño que el cambio en\(d\) será prácticamente insignificante, por lo que se puede tratar\(F^G\), y por lo tanto\(\tau_{ext}\), como una constante. Entonces la situación es análoga a la de un oscilador sometido a una fuerza externa constante (sección 11.2): la frecuencia de las oscilaciones no cambiará, sino que la posición de equilibrio sí. En la Ecuación (11.2.14) encontramos que\(y_{0}^{\prime}-y_{0}=F_{e x t} / k\) para un resorte de constante de resorte\(k\), donde\(y_0\) estaba la antigua y\(y_{0}^{\prime}\) la nueva posición de equilibrio (la fuerza era igual a\(−mg\); el desplazamiento de la posición de equilibrio será en la dirección de la fuerza). Para el balance de torsión, el resultado equivalente es

\[ \theta_{0}^{\prime}-\theta_{0}=\frac{\tau_{e x t}}{\kappa}=\frac{F^{G} l}{\kappa} \label{eq:11.38} .\]

Entonces, si se mide el desplazamiento angular de la posición de equilibrio, se puede obtener\(F^G\). Este desplazamiento va a ser muy pequeño, pero puedes intentar monitorear la posición de la mancuerna, por ejemplo, reflejando un láser de ella (o, una o ambas de tus pequeñas masas podrían ser un láser pequeño). Al rastrear las oscilaciones del punto de luz láser en la pared, es posible que pueda detectar el desplazamiento muy pequeño predicho por la ecuación (\ ref {eq:11.38}).