4.3: Bifurcación y Atrayentes Puntuales

Nuevos fenómenos interesantes, como la bifurcación y los atractores, ocurren cuando la no linealidad es grande. En el capítulo\(3\) se mostró que el diagrama estado-espacio\(\left( \dot{x},x\right)\) para un oscilador armónico no amortiguado es una elipse con dimensiones definidas por la energía total del sistema. Como se muestra en la figura (3.5.1), para el oscilador armónico amortiguado, el diagrama estado-espacio gira hacia adentro al origen debido a la disipación de energía. La no linealidad distorsiona la forma de la elipse o espiral en el diagrama estado-espacio, y así los diagramas estado-espacio, o espacio de fase correspondiente, proporcionan representaciones útiles del movimiento de sistemas periódicos lineales y no lineales.

El complicado movimiento de los sistemas no lineales hace necesario distinguir entre el comportamiento transitorio y asintótico. El oscilador armónico amortiguado ejecuta un movimiento espiral transitorio que se aproxima asintóticamente al origen. El comportamiento transitorio depende de las condiciones iniciales, mientras que el límite asintótico de la solución de estado estacionario es una ubicación específica, que se denomina atractor puntual. El atractor puntual para movimiento amortiguado en el pozo de potencial anarmónico

\[U(x)=2x^{2}+x^{4}\]

está en el mínimo, que es el origen del diagrama estado-espacio como se muestra en la figura (4.2.1).

El pozo de potencial unidimensional más complicado

\[U(x)=8-4x^{2}+0.5x^{4}\]

mostrado en la Figura\(\PageIndex{1}\), tiene dos mínimos que son simétricos alrededor\(x=0\) con un sillín de altura\(8\).

Las energías cinéticas más potenciales de una partícula con masa\(m=2,\) liberada en este potencial, se asumirán dadas por

\[E(x,\dot{x})=\dot{x}^{2}+U(x)\]

La gráfica estado-espacio en la Figura\(\PageIndex{1}\) muestra contornos de energía constante con los mínimos en\((x,\dot{x})=(\pm 2,0)\). A una energía total ligeramente mayor, los contornos son bucles cerrados alrededor de cualquiera de los dos mínimos en\( x=\pm 2\). A las energías totales por encima de la silla de montar\(8\) la energía de los contornos son en forma de cacahuete y son simétricas sobre el origen. Suponiendo que el movimiento está débilmente amortiguado, entonces una partícula liberada con energía total\(E_{total}\) que es mayor que\(E_{saddle}\) seguirá una trayectoria espiral en forma de cacahuete centrada en\((x,\dot{x})=(0,0)\) en el diagrama estado-espacio para\( E_{total}>E_{saddle}\). Para\(E_{total}<E_{saddle}\) hay dos soluciones separadas para los dos mínimos centrados en\(x=\pm 2\) y\(\dot{x} =0\). Este es un ejemplo de bifurcación donde la única solución para\( E_{total}>E_{saddle}\) se bifurca en cualquiera de las dos soluciones para\( E_{total}<E_{saddle}\).

Figura\(\PageIndex{1}\): El lado izquierdo muestra la energía potencial para un potencial simétrico bimodal\(U(x) = 8 - 4x^2 + 0.5x^4\). La figura derecha muestra los contornos de la suma de energías cinéticas y potenciales en un diagrama estado-espacio. Para las energías totales por encima del punto de sillín, la partícula sigue trayectorias en forma de cacahuete en el espacio de estado centrado alrededor\((x,\dot{x}) = (0, 0)\). Para las energías totales por debajo del punto de sillín, la partícula tendrá trayectorias cerradas alrededor de cualquiera de los dos mínimos simétricos ubicados en\((x, \dot{x}) = (\pm 2, 0)\). Así, la solución del sistema se bifurca cuando la energía total está por debajo del punto de sillín.

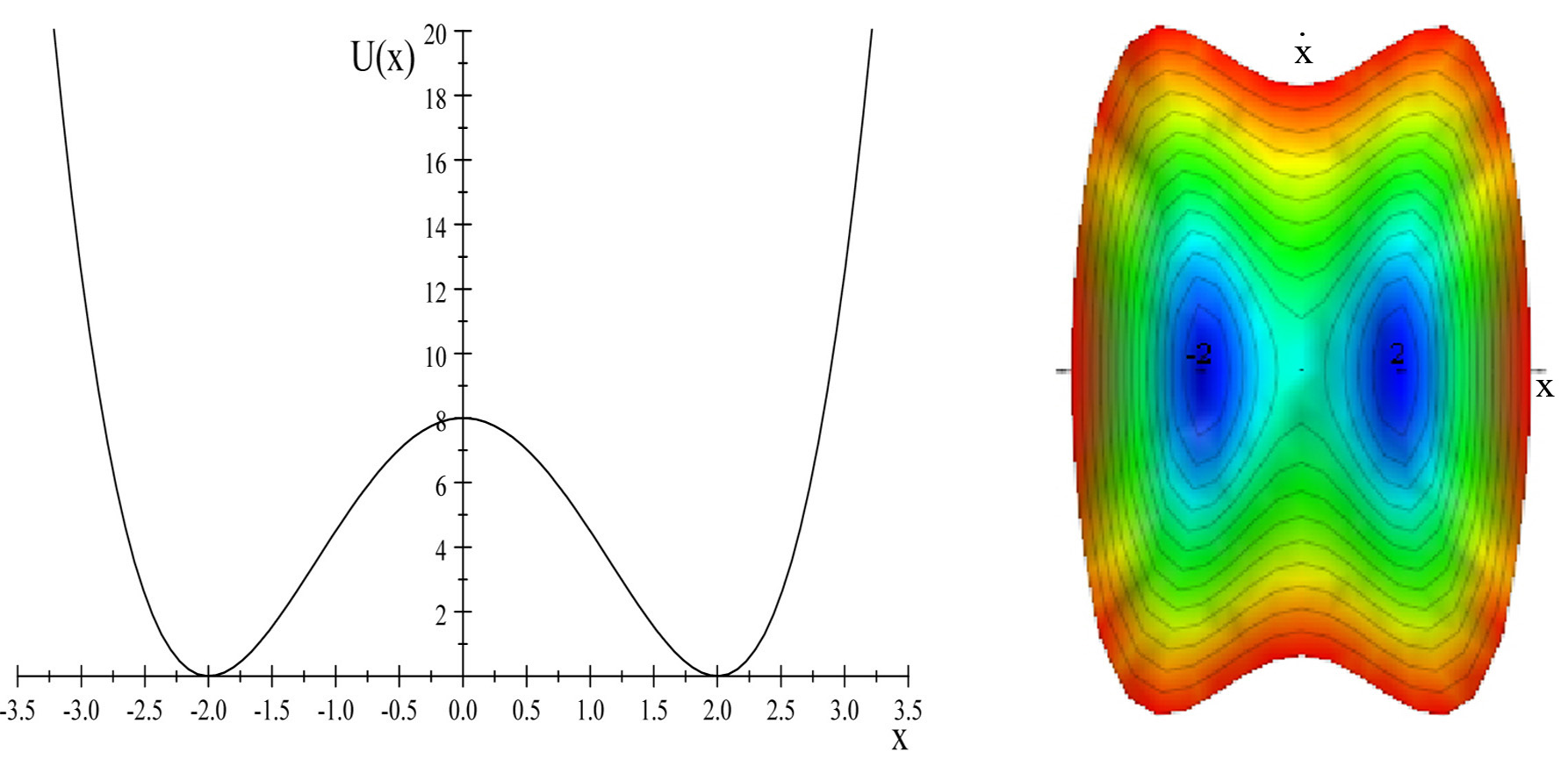
Para una\(E_{total}>E_{saddle},\) amortiguación inicial de energía total dará como resultado trayectorias espirales de la partícula que quedarán atrapadas en uno de los dos mínimos. Para\(E_{total}>E_{saddle}\) las trayectorias de las partículas están centradas dando la impresión de que terminarán en el\((x,\dot{x})=(0,0)\) momento en que se disipe la energía cinética. Sin embargo, para\(E_{total}<E_{saddle}\) la partícula quedará atrapada en uno de los dos mínimos y la trayectoria terminará en la parte inferior de ese mínimo de energía potencial que ocurre en\((x, \dot{x})=(\pm 2,0)\). Estos dos posibles puntos terminales de la trayectoria se denominan atractores puntuales. Este ejemplo parece tener un solo atractor para el\(E_{total}>E_{saddle}\) cual se bifurca conduciendo a dos atractores a\((x,\dot{x})=(\pm 2,0)\) for\(E_{total}<E_{saddle}\). La determinación de qué mínimo atrapa una partícula dada depende exactamente de dónde comienza la partícula en el espacio de estado y la amortiguación etc. Es decir, para este caso, donde hay simetría alrededor del\(x\) eje, la partícula tiene una energía total inicial\(E_{total}>E_{saddle},\) luego las condiciones iniciales con \(\pi\)radianes del espacio estatal conducirán a trayectorias que quedan atrapadas en el mínimo izquierdo, y los otros\(\pi\) radianes del espacio estatal quedarán atrapados en el mínimo derecho. Las trayectorias que comienzan cerca de la división entre estas dos mitades del espacio del estado inicial serán sensibles a la fase de inicio exacta. Este es un ejemplo de sensibilidad a las condiciones iniciales.