1.3: Medición

Objetivos de aprendizaje

• Medición para la relatividad

Nos gustaría tener un sistema general de medición para la relatividad, pero hasta el momento sólo tenemos un patchwork incompleto. La longitud de un vector similar al tiempo se puede definir como el tiempo medido en un reloj que se mueve a lo largo del vector. Un vector espacial tiene una longitud que se mide en una regla cuyo movimiento es tal que en el marco de referencia de la regla, los puntos finales del vector son simultáneos. Pero no existe un tercer instrumento de medición diseñado con el propósito de medir vectores parecidos a la luz.

Tampoco conseguimos automágicamente un sistema completo de medición solo por haber definido las coordenadas de Minkowski. Por ejemplo, todavía no sabemos cómo encontrar la longitud de un vector temporal como\((\Delta t,\Delta x) = (2,1)\), y sospechamos que no será igual\(2\), ya que el experimento de Hafele-Keating nos dice que un reloj sometido al movimiento representado por probablemente no\(\Delta x = 1\) estará de acuerdo con un reloj llevado por el observador cuyo reloj usamos para definir estas coordenadas.

Invariantes

Todo el tema de la medición es apto para ser confuso, porque el paisaje cambiante de la relatividad nos hace sentir como si hubiéramos entrado en un paisaje de Salvador Dalí de derretimiento de relojes de bolsillo. Una buena manera de recuperar nuestro rumbo es buscar cantidades que sean invariantes: son las mismas en todos los marcos de referencia. Una invariante euclidiana, como una longitud o un ángulo, es aquella que no cambia bajo rotaciones: todos los observadores coinciden en su valor, independientemente de las orientaciones de sus marcos de referencia. Para una invariante relativista, requerimos además que los observadores estén de acuerdo sin importar el estado de movimiento que tengan. (Una transformación que cambia de un marco inercial de referencia a otro, sin ninguna rotación, se llama impulso.)

La carga eléctrica es un buen ejemplo de una invariante. Los electrones en los átomos suelen tener velocidades de\(0.01\) a\(0.1\) (en nuestras unidades relativistas, donde \(c = 1\)), por lo que si la carga de un electrón dependiera de su movimiento relativo a un observador, los átomos no serían eléctricamente neutros. Se han realizado experimentos para probar esto con la fenomenal precisión de una parte en\(10^{21}\), con resultados nulos.

Un vector nunca puede ser un invariante, ya que cambia de dirección bajo una rotación. (Algunos vectores, como las velocidades, también cambian bajo un impulso). En la mecánica de primer año, cualquier cantidad, como la energía, que no fuera un vector generalmente caía en la categoría a la que nos referíamos como escalares. En relatividad, sin embargo, el término “escalar” tiene una definición mucho más restrictiva, que discutiremos en la sección 6.2.

Por cierto, los principiantes en la relatividad a veces se confunden sobre la invarianza en lugar de la conservación. No son lo mismo, y tampoco implica lo otro. Por ejemplo, el momentum tiene una dirección en el espacio, por lo que claramente no es invariante —pero veremos en la sección 4.3 que existe una versión relativista del vector momentum que se conserva. Al igual que en la mecánica newtoniana, no nos importa si todos los observadores coinciden en el impulso de un sistema —solo nos importa que la ley de conservación del impulso sea válida y tenga la misma forma en todos los marcos. Por el contrario, hay cantidades que son invariantes pero no conservadas, siendo la masa un ejemplo.

La métrica

Figura\(\PageIndex{1}\): Los dos rectángulos de luz tienen la misma área.

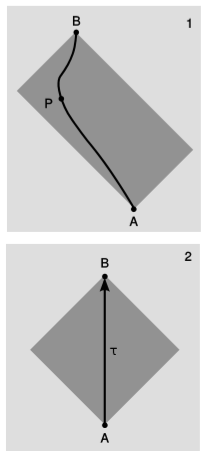
El área en\(1+1\) dimensiones también es una invariante, como se demuestra en la sección 2.5. La invarianza de área tiene poca importancia por sí sola, pero proporciona un buen escalón hacia un sistema relativista de medición. Supongamos que tenemos eventos\(A\) (Carlos VII es restaurado al trono) y\(B\) (Juana de Arco es ejecutada). Ahora imagina que los extraterrestres tecnológicamente avanzados quieren estar presentes en ambos\(A\) y\(B\), pero en el ínterin desean huir en su nave espacial, estar presentes en algún otro evento\(P\) (tal vez una conferencia de prensa en la que dan una actualización sobre los eventos que tienen lugar en la tierra), pero regresen a tiempo para\(B\). Ya que nada puede ir más rápido que\(c\) (que tomamos para igualar\(1\)),\(P\) no puede estar demasiado lejos. El conjunto de todos los eventos posibles\(P\) forma un rectángulo, figura\(\PageIndex{1}\), en el plano\(1+1\) -dimensional que tiene\(A\) y\(B\) en esquinas opuestas y cuyos bordes tienen pendientes iguales a\(\pm 1\). Llamamos a este tipo de rectángulo un rectángulo claro.

El área de este rectángulo será la misma independientemente del marco de referencia de uno. En particular, podríamos elegir un marco especial de referencia, panel\(2\) de la figura, tal que\(A\) y\(B\) se produzcan en el mismo lugar. (No ocurren en el mismo lugar, por ejemplo, en el marco del sol, porque la tierra está girando y dando vueltas alrededor del sol). Dado que la velocidad \(c = 1\)es la misma en todos los marcos de referencia, y los lados del rectángulo tenían pendientes\(\pm 1\) en marco\(1\), aún deben tener pendientes\(\pm 1\) en marco\(2\). El rectángulo se convierte en un cuadrado, cuyas diagonales son a\(o\) y a\(s\) para marco\(2\). La longitud de estas diagonales es igual al tiempo\(\tau\) transcurrido en un reloj que está en reposo en cuadro\(2\), es decir, un reloj que se desliza por el espacio a velocidad constante desde\(A\) hasta\(B\), reuniéndose con el planeta tierra cuando su órbita lo lleva a\(B\). El área de las regiones grises se puede interpretar como la mitad del cuadrado de este tiempo de reloj deslizable, que se llama el tiempo adecuado. “Propio” se usa aquí en el sentido algo arcaico de “propio” o “yo”, como en “El Vaticano no se encuentra dentro de Italia propiamente dicha. ” El tiempo adecuado, que anotamos\(\tau\), solo se puede definir para líneas mundiales similares a tiempo, ya que una línea mundial similar a la luz o al espacio no es posible para un reloj material.

En términos de coordenadas (Minkowski), supongamos que los eventos\(A\) y\(B\) están separados por una distancia\(x\) y un tiempo\(t\). Entonces en general\(t^2 - x^2\) da el cuadrado del tiempo del reloj deslizable.

Prueba: Por la forma en que el área se escala con una reescalación de las coordenadas, la expresión debe tener la forma\((...)t^2+(...)tx+(...)x^2\), donde cada una\((...)\) representa una constante sin unidades. El\(tx\) coeficiente debe ser cero por la isotropía del espacio. El\(t^2\) coeficiente debe ser igual\(1\) para dar la respuesta correcta en el caso de\(x = 0\), donde las coordenadas son las de un observador en reposo relativo al reloj. Dado que el área se desvanece para\(x = t\), el\(x^2\) coeficiente debe ser igual\(-1\). Cuando\(|x|\) es mayor que\(|t|\), eventos\(A\) y\(B\) están tan separados en el espacio y tan cercanos en el tiempo que sería imposible tener una relación de causa y efecto entre ellos, ya que\(c = 1\) es la velocidad máxima de causa y efecto. En esta situación\(t^2 - x^2\) es negativa y no puede interpretarse como un tiempo de reloj, sino que puede interpretarse como menos el cuadrado de la distancia entre\(A\) y\(B\), como se mide en un marco de referencia en el que\(A\) y\(B\) son simultáneos.

Generalizando a\(3+1\) dimensiones y a cualquier vector\(v\), no solo a un desplazamiento en el espacio-tiempo, tenemos una medida del vector definido por

\[ v^{2}_{t} - v^{2}_{x} - v^{2}_{y} - v^{2}_{z} \]

En el caso especial donde \(v\)es un desplazamiento espacio-tiempo, esto puede ser referido como el intervalo espacio-tiempo. A excepción de los signos, esto se parece mucho al teorema de Pitágoras, que es un caso especial del producto vector dot. Por lo tanto, definimos una función\(g\) llamada métrica

\[ g( \textbf {u}, \textbf {v}) = u_{t}v_{t} - u_{x}v_{x} - u_{y}v_{y} - u_{z}v_{z} \]

Debido a la analogía con el producto punto euclidiano, a menudo usamos la notación\(u\cdot v\) para esta cantidad, y a veces lo llamamos el producto interno. La métrica es el objeto central de la relatividad. En general la relatividad, que describe a la gravedad como una curvatura del espacio-tiempo, los coeficientes que ocurren en el lado derecho ya no son\(\pm 1\), sino que deben variar de punto a punto. Incluso en la relatividad especial, donde los coeficientes pueden hacerse constantes, la definición de\(g\) es arbitraria hasta una constante multiplicativa distinta de cero, y en particular muchos autores definen\(g\) como el negativo de nuestra definición. La convención de signos que utilizamos es la más común en física de partículas, mientras que lo contrario es más común en la relatividad clásica. El conjunto de signos,\(+---\) o\(-+ ++\), se llama la firma de la métrica. En la sección 1.1 desarrollamos la idea de ortogonalidad de vectores espacio-tiempo, con la interpretación física de que si un observador se mueve a lo largo de un vector\(o\), un vector s que es ortogonal a\(o\) es un vector de simultaneidad. Esto corresponde a la fuga del producto interno,\(o\cdot s = 0\), y sólo es imperfectamente análogo a la idea de que los vectores euclidianos son perpendiculares si su producto punto es cero. En particular, un vector euclidiano distinto de cero nunca es perpendicular a sí mismo, sino para cualquier vector similar a la luz que\(v\) tengamos\(v\cdot v = 0\). La métrica no nos da una medida de la longitud de los vectores similares a la luz. Físicamente, ni una regla ni un reloj pueden medir tal vector.

La métrica en unidades SI

Las unidades con\(c = 1\) son conocidas como unidades naturales. (Son naturales a la relatividad en el mismo sentido que las unidades con\(\tilde{h} = 1\) son naturales a la mecánica cuántica.) Cualquier ecuación expresada en unidades naturales puede ser reexpresada en unidades SI por el simple procedimiento de insertar factores de\(c\) donde sea necesario para obtener unidades que tengan sentido. El resultado para la métrica podría ser

\[g( \textbf{u}, \textbf{v}) = c^{2}u_{t}v_{t} - u_{x}v_{x} - u_{y}v_{y} - u_{z}v_{z}\]

o

\[g(\textbf{u},\textbf{v}) = u_{t}v_{t} - (u_{x}v_{x} - u_{y}v_{y} - u_{z}v_{z})/c^{2}\]

No importa cuál escojamos, ya que la métrica es arbitraria hasta un factor constante. La primera expresión da un resultado en metros, los segundos segundos segundos.

Rayos de luz ortogonales

En un diagrama de espacio-tiempo en\(1+1\) dimensiones, representamos el cono de luz con las dos líneas\(x = \pm t\), dibujadas en un ángulo de\(90\) grados relativo entre sí. ¿Estas líneas son ortogonales? .

No. Por ejemplo, si\(u = (1,1)\) y\(v = (1,-1)\), entonces\(u\cdot v\) es\(2\), no cero.

Pioneer 10

La sonda espacial Pioneer 10 se lanzó en 1972, y en 1973 fue la primera nave que voló por el planeta Júpiter. Cruzó la órbita del planeta Neptuno en 1983, después de lo cual se recibieron datos de telemetría hasta 2002. El siguiente cuadro da la posición de la nave espacial con respecto al sol exactamente a la medianoche del 1 de enero de 1983 y el 1 de enero de 1995. Se toma para ser la fecha de 1983\(t = 0\).

t (s)	x	y	z
0	1.784 × 10 ^12 m	3.951 × 10 ^12 m	0.237 × 10 ^12 m
3.7869 × 10 ^8 s	2.420 × 10 ^12 m	8.827 × 10 ^12 m	0.488 × 10 ^12 m

Compara el tiempo transcurrido en la nave espacial con el tiempo en un marco de referencia atado al sol.

Podemos convertir estos datos en unidades naturales, siendo la unidad de distancia la segunda (es decir, una luz-segundo, la distancia que la luz recorre en un segundo) y siendo la unidad de tiempo segundos. Convirtiendo y llevando a cabo esta resta, tenemos:

\( \Delta t \)	\( \Delta x \)	\( \Delta y \)	\( \Delta z \)
3.786912 × 10 ^8 s	0.2121 × 10 ^4 s	1.626 × 10 ^4 s	0.084 × 10 ^4 s

Comparando los exponentes de los números temporales y espaciales, podemos ver que la nave espacial se movía a una velocidad del orden de la velocidad\(10^{-4}\) de la luz, por lo que los efectos relativistas deberían ser pequeños pero no completamente despreciables. Dado que el intervalo es parecido al tiempo, podemos tomar su raíz cuadrada e interpretarla como el tiempo transcurrido en la nave espacial. El resultado es\(\tau = 3.786911996×108\, s\). Esto es\(0.4\, s\) menor que el tiempo transcurrido en el marco de referencia del sol.

El Factor Gamma

Figura\(\PageIndex{2}\): La “paradoja” gemela.

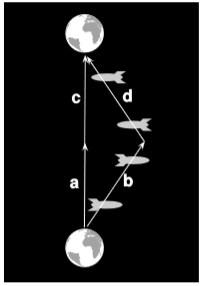
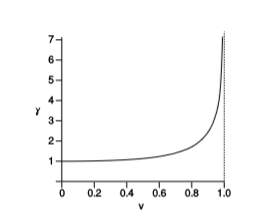
La figura\(\PageIndex{2}\) es la versión relativista del ejemplo 1.1.1. Pretendemos analizarlo usando la métrica, y dado que la métrica da el mismo resultado en cualquier marco, hemos elegido por conveniencia representarlo en el marco en el que la tierra está en reposo. Tenemos\(a = (t,0)\) y\(b = (t,vx)\), donde\(v\) esta la velocidad de la nave espacial relativa a la tierra. La aplicación de la métrica da tiempo adecuado\(t\) para el gemelo terrestre y\(t \sqrt{1-v^{2}}\) para el gemelo viajero. Los mismos resultados se aplican para\(c\) y\(d\). El resultado es que el gemelo terrestre experimenta un tiempo que es mayor por un factor\(\gamma\) (letra griega gamma) definido como\(\gamma = 1/ \sqrt{1-v^{2}}\). Si\(v\) está cerca\(c\),\(\gamma\) puede ser grande, y encontramos que cuando el gemelo astronauta regresa a casa, aún juvenil, el gemelo terrestre puede ser viejo y gris. Esto fue en un momento referido como la paradoja de los gemelos, y se consideró paradójica ya sea porque parecía desafiar el sentido común o porque la gemela viajera podía argumentar que ella era la que estaba en reposo mientras la tierra se movía. La violación del sentido común es de hecho lo que se observó en el experimento de Hafele-Keating, y este último argumento es falaz por las mismas razones que en la versión galileana dada en el ejemplo 1.1.1.

Tenemos en general la siguiente interpretación:

Dilatación del tiempo

Un reloj corre más rápido en el marco de referencia de un observador que está en reposo en relación con el reloj. Un observador en movimiento relativo al reloj a velocidad\(v\) percibe que el reloj corre más lentamente por un factor de\(\gamma\).

Figura\(\PageIndex{3}\): Una gráfica de\(\gamma\) como una función de\(v\).

A pesar de que esto se expresa en términos de relojes, lo interpretamos como que nos dice algo sobre el tiempo mismo. La actitud es que debemos definir un concepto en términos de las operaciones requeridas para medirlo: el tiempo se define como lo que mide un reloj. Esta filosofía, que ha sido inmensamente influyente entre los físicos, se llama operacionalismo y fue desarrollada por P.W. Bridgman en la década de 1920. Nuestra definición operativa del tiempo funciona porque las tasas de todos los procesos físicos se ven afectadas por igual por la dilatación del tiempo. Para cuando los gemelos en figura\(\PageIndex{2}\) se reúnan, no sólo la gemela viajera ha escuchado menos garrapatas de su antiguo reloj de bolsillo mecánico, sino que también ha tenido menos latidos cardíacos, y el reloj atómico de la nave concuerda con su reloj dentro de la precisión del reloj.

La dilatación del tiempo es simétrica en el sentido de que trata democráticamente todos los marcos de referencia. Si los observadores\(A\) y\(B\) no están en reposo uno respecto al otro, entonces\(A\) dice que\(B’s\) el tiempo corre lento, pero\(B\) dice que\(A\) es el lento. En la figura\(\PageIndex{2}\), las leyes de la física no hacen distinción entre los marcos de referencia que coinciden con los vectores\(a\) y\(b\); como en el caso galileano correspondiente del ejemplo 1.1.1, la asimetría se produce porque\(a\) y\(c\) son paralelos, pero \(b\)y no lo\(d\) son.

Como se muestra en el ejemplo\(\PageIndex{4}\) a continuación, la consistencia exige que además del efecto en el tiempo tengamos un efecto similar en las distancias:

Contracción de longitud

Un medidor de palo aparece más largo para un observador que está en reposo relativo a él. Un observador que se mueve en relación con el medidor de palo en\(v\) observes the stick to be shortened by a factor of \(\gamma\).

La visualización de la contracción de longitud en términos de diagramas espacio-tiempo se presenta en la figura 1.4.3. Nuestra discusión actual se limita a\(1+1\) las dimensiones, pero en\(3+1\), solo se contrae la longitud a lo largo de la línea de movimiento.

Un viaje interestelar

Alice se queda en la tierra mientras su gemela Betty se dirige en una nave espacial a Tau Ceti, una estrella cercana. Tau Ceti es\(12\) light-years away, so even though Betty travels at \(87\%\) of the speed of light, it will take her a long time to get there: \(14\) years, according to Alice.

Figura \(\PageIndex{4}\): Un viaje interestelar

Betty experimenta dilatación del tiempo. A esta velocidad, ella\(\gamma\) es\(2.0\), por lo que el viaje sólo le parecerá que dure\(7\) años. Pero hay una simetría perfecta entre los marcos de referencia de Alice y Betty, por lo que Betty está de acuerdo con Alice en su velocidad relativa. Betty se ve a sí misma como en reposo, mientras que el sol y Tau Ceti se mueven hacia atrás a\(87\%\) la velocidad de la luz. ¿Cómo, entonces, puede observar a Tau Ceti para llegar a ella en solo\(7\) años, cuando debería tomar\(14\) años viajar\(12\) años luz a esta velocidad?

Tenemos que tener en cuenta la contracción de longitud. Betty ve que la distancia entre el sol y Tau Ceti se reduce en un factor de\(2\). Lo mismo ocurre para Alice, quien observa que Betty y su nave espacial sean escorzadas.

Un reloj atómico en movimiento

Figura\(\PageIndex{5}\): Dilatación del tiempo medida con un reloj atómico a bajas velocidades. La curva teórica, mostrada con una línea discontinua, se calcula a partir de\(\gamma = 1/\sqrt{1 - v^2}\); a estas pequeñas velocidades, la aproximación\(\gamma \approx 1 + v^{2}/2\) es excelente, y la gráfica es indistinguible de una parábola. Esta gráfica corresponde a una vista extrema de primer plano de la esquina inferior izquierda de la figura\(\PageIndex{3}\). Las barras de error en los puntos experimentales son aproximadamente del mismo tamaño que los puntos.

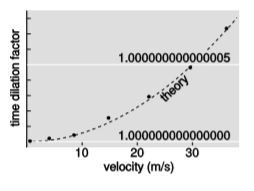
Al expandirse\(\gamma\) en una serie Taylor\(\gamma \approx 1 - v^{2}/2\), so that when \(v\) is small, relativistic effects are approximately proportional to \(v^2\), encontramos, por lo que es muy difícil observarlos a bajas velocidades. Esta fue la razón por la que el experimento de Hafele-Keating se realizó a bordo de aviones de pasajeros, que fluyen a altas velocidades. Los chorros, sin embargo, fluyen a gran altura, y esto trae un efecto de dilatación por segunda vez, uno de relación general de visión debido a la gravedad. El propósito principal del experimento fue en realidad probar este efecto. No fue sino hasta cuatro décadas después de Hafele y Keating que cualquiera hizo un experimento conceptualmente simple de reloj atómico en el que el único efecto era el movimiento, no la gravedad. En 2010, sin embargo, Chou et al.7 lograron construir un reloj atómico lo suficientemente preciso como para detectar dilatación del tiempo a velocidades tan bajas como\(10\, m/s\). Figure \(\PageIndex{5}\) muestran sus resultados. Como no era práctico mover todo el reloj, los experimentadores solo movieron los átomos de aluminio dentro del reloj que en realidad lo hicieron “marcar”.

Dilatación a gran escala

Los efectos de dilatación temporal descritos en el ejemplo\(\PageIndex{5}\) fueron muy pequeños. Si queremos ver un gran efecto de dilatación en el tiempo, no podemos hacerlo con algo del tamaño de los relojes atómicos que usaron; la energía cinética sería mayor que el megatonaje total de todos los arsenales nucleares del mundo. Podemos, sin embargo, acelerar las partículas subatómicas a velocidades a las que\(\gamma\) es grande. Para los físicos experimentales de partículas, la relatividad es algo que haces todo el día antes de regresar a casa y hacer una parada en la tienda de leche. Un experimento temprano de baja precisión de este tipo fue realizado por Rossi y Hall en 1941, utilizando rayos cósmicos naturales. La figura\(\PageIndex{6}\) muestra un experimento de 1974 de tipo similar que verificó la dilatación temporal predicha por la relatividad con una precisión de aproximadamente una parte por mil.

Figura\(\PageIndex{6}\): Izquierda: Aparato utilizado para la prueba de dilatación relativista del tiempo descrita en este ejemplo. Los bloques prominentes en blanco y negro son grandes imanes que rodean una tubería circular con vacío en su interior. c) 1974 por el CERN. Derecha: Los muones aceleraron para casi\(c\) sufrir desintegración radiactiva mucho más lentamente de lo que lo harían según un observador en reposo con respecto a los muones. Los dos primeros puntos de datos (círculos sin relleno) fueron sometidos a grandes errores sistemáticos.

Las partículas llamadas muones (que llevan el nombre de la letra griega\(\mu\), “myoo”) fueron producidas por un acelerador en el CERN, cerca de Ginebra. Un muón es esencialmente una versión más pesada del electrón. Los muones sufren desintegración radiactiva, durando un promedio de solo\(2.197\, µs\) before they evaporate into an electron and two neutrinos. The 1974 experiment was actually built in order to measure the magnetic properties of muones, pero produjo una prueba de alta precisión de dilatación del tiempo como subproducto. Debido a que los muones tienen la misma carga eléctrica que los electrones, pueden quedar atrapados usando campos magnéticos. Los muones fueron inyectados en el anillo que se muestra en la figura \(\PageIndex{6}\), dando vueltas alrededor del mismo hasta que sufrieron desintegración radiactiva. A la velocidad a la que viajaban estos muones, tenían\(\gamma = 29.33\), por lo que en promedio duraron\(29.33\) times longer than the normal lifetime. In other words, they were like tiny alarm clocks that autodestruidos en un momento seleccionado al azar. La gráfica muestra el número de desintegraciones radiactivas contadas, en función del tiempo transcurrido después de que una determinada corriente de muones fue inyectada en el anillo de almacenamiento. Las dos líneas discontinuas muestran las tasas de decaimiento predichas con y sin relatividad. La línea relativista es la que concuerda con el experimento.