Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.E: Espacio-tiempo (Ejercicios)

Última actualización

30 oct 2022
Guardar como PDF
- 1.5: Triángulo y Desigualdades Cauchy-Schwarz
- 2: Fundaciones

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Q1

Los astronautas en tres naves espaciales diferentes se están comunicando entre sí. Aquellos a bordo de los barcos $A$ y $B$ están de acuerdo en la velocidad a la que pasa el momento, pero no están de acuerdo con los que están en barco $C$ .

Alice está a bordo del barco $A$ . ¿Cómo describe el movimiento de su propia nave, en su marco de referencia?
Describir el movimiento de los otros dos barcos según Alice.
Dar la descripción según Betty, cuyo marco de referencia es la nave $B$ .
Haz lo mismo con Cathy, a bordo del barco $C$ .

Q2

Qué sucede en la ecuación para $\gamma$ when you put in a negative number for $v$ ? Explain what this means physically, and why it makes sense.

Q3

La sonda $1$ espacial Voyager, lanzada en 1977, se mueve más rápido en relación con la tierra que cualquier otro objeto hecho por el hombre, a $17,000$ metros por segundo.

Calcular las sondas $\gamma$ .
En el transcurso de un año en la tierra, pasa poco menos de un año en la sonda. ¿Cuánto menos? (Hay $31$ millones de segundos en un año).

Q4

La tierra está orbitando el sol, y por lo tanto se contrae relativisticamente en la dirección de su movimiento. Calcule la cantidad en la que su diámetro se contrae en esta dirección.

Q5

La figura muestra siete vectores de desplazamiento en espacio-tiempo. ¿Cuáles de estos representan intervalos espacio-tiempo que son iguales entre sí?

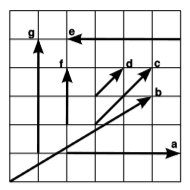
higo 1.e.1.png

Q6

En geometría euclidiana en tres dimensiones, supongamos que tenemos dos vectores, $a$ and $b$ , which are unit vectors, i.e., $a \cdot a = 1$ and $b \cdot b = 1$ . What is the range of possible values for the inner product $a \cdot b$ ?
Repita la parte a para dos vectores unitarios orientados al futuro, similares al tiempo en $3 + 1$ dimensions.

Q7

Expresada en unidades naturales, la transformación de Lorentz es

$t' = \gamma t - v\gamma x' \\ x' = -v\gamma t + \gamma x$

Insertar factores de $c$ to make it valid in units where $c \neq 1$.
Demostrar que en el límite $c \rightarrow \infty$ , estos tienen el comportamiento rig ht galileo.

Q8

Este problema supone que tienes algunos conocimientos básicos de la física cuántica. Una forma de expresar el principio de correspondencia tal como se aplica a la relatividad especial es que en el límite $c \rightarrow \infty$ , todas las expresiones relativistas tienen que pasar a sus contrapartes galileanas. ¿Cuál sería el límite correspondiente si quisiéramos recuperar la mecánica clásica de la mecánica cuántica?

Q9

En $3 + 1$ dimensiones, demuestre que si $\overrightarrow{u}$ y $\overrightarrow{v}$ son distintos de cero, futuro-ligeros, y no paralelos entre sí, entonces su suma es futuro-tiempo.

Q10

Demostrar que si $\overrightarrow{u}$ y $\overrightarrow{v}$ son distintos de cero, parecidos a la luz y ortogonales entre sí, entonces son paralelos, es decir, $\overrightarrow{u} = c \overrightarrow{v}$ para algunos $c \neq 0$ .

Q11

La velocidad a la que una perturbación viaja a lo largo de una cuerda bajo tensión viene dada por $v = \sqrt{\frac{T}{\mu}}$ , dónde $\mu$ está la masa por unidad de longitud, y $T$ es la tensión.

Supongamos que una cuerda tiene una densidad $\rho$ , y un área transversal A. Encuentra una expresión para la tensión máxima que posiblemente pueda existir en la cuerda sin producir $v > c$ , lo cual es imposible según la relatividad. Exprese su respuesta en términos de $\rho$ , A, y $c$ . La interpretación es que la relatividad pone un límite a lo fuerte que puede ser cualquier material.
Cada sustancia tiene una resistencia a la tracción, definida como la fuerza por unidad de área requerida para romperla al separarla. La resistencia a la tracción se mide en unidades de $N/m^2$ , que es la misma que el pascal ( $Pa$ ), la unidad de presión mks. Hacer una estimación numérica de la resistencia máxima a la tracción permitida por la relatividad en el caso en que la cuerda esté hecha de materia ordinaria, con una densidad del mismo orden de magnitud que la del agua. (A modo de comparación, el kevlar tiene una resistencia a la tracción de aproximadamente $4 \times 10^9\: Pa$ , y se especula que las fibras hechas de nanotubos de carbono podrían tener valores tan altos como $6 \times 10^{10}\: Pa$ .)
Un agujero negro es una estrella que se ha derrumbado y se ha vuelto muy densa, por lo que su gravedad es demasiado fuerte para que cualquier cosa pueda escapar de él. Por ejemplo, la velocidad de escape de un agujero negro es mayor que $c$ , por lo que un proyectil no puede ser disparado fuera de él. Muchas personas, cuando escuchan esta descripción de un agujero negro en términos de una velocidad de escape mayor que $c$ , se preguntan por qué todavía no sería posible extraer un objeto de un agujero negro por otros medios que no sean lanzarlo como proyectil. Por ejemplo, supongamos que bajamos a un astronauta en un agujero negro en una cuerda, y luego lo sacamos de nuevo. ¿Por qué no podría funcionar esto?

Q12

La varilla en la figura es perfectamente rígida. En caso de $A$ , the hammer strikes one end of the rod. At event $B$ , the other end moves. Since the rod is perfectly rigid, it can’t compress, so $A$ and $B$ are simultaneous. In frame $2$ , $B$ happens before $A$ . Did the motion at the right end hacer que la persona de la izquierda decida recoger el martillo y usarlo?

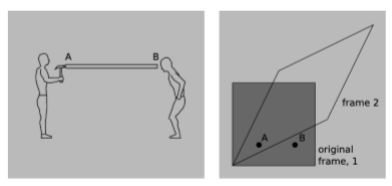
higo 1.e.2.png

Q13

Utilice un diagrama de espacio-tiempo para resolver la siguiente paradoja de la relatividad. Relatividad dice que en un marco de referencia, evento $A$ could happen before event $B$ , but in someone else’s frame $B$ would come before $A$ . How can this be? Obviously the two people could meet up at $A$ and talk as they cruised past each other. Wouldn’t they have to agree on whether $B$ had already happened?

Q14

The grid represents spacetime in a certain frame of reference. Event $A$ is marked with a dot. Mark additional points satisfying the following criteria. (Pick points that lie at the intersections of the gridlines.)

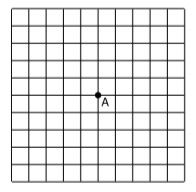
fig 1.E.3.png

Punto $B$ is at the same location as $A$ in this frame of reference, and lies in its future.
$C$ is also in point $A$ ’s future, is not at the same location as $A$ in this frame, but is in the same location as $A$ according to some other frame of reference.
$D$ is simultaneous with $A$ in this frame of reference.
$E$ is not simultaneous with $A$ in this frame of reference, but is simultaneous with it according to some other frame.
$F$ lies in $A$ ’s past according to this frame of reference, but could not have caused $A$ .
$G$ lies in $A$ ’s future according to this frame of reference, but is in its past according to some other frames.
$H$ lies in $A$ ’s future according to any frame of reference, not just this one.
$I$ is the departure of a spaceship, which arrives at $A$ .
$J$ could have caused $A$ , but could not have been the departure of a spaceship like $I$ that arrived later at $A$ .

Q15

Dado un observador cuya línea mundial está a lo largo de un cuatro vectores $\overrightarrow{O}$ , supongamos que queremos determinar si algún otro cuatro vector $\overrightarrow{P}$ es también una posible línea mundial de un observador. Demostrar que el conocimiento de los signos de los productos internos $\overrightarrow{O} \cdot \overrightarrow{P}$ y $\overrightarrow{P} \cdot \overrightarrow{P}$ es necesario y suficiente para determinarlo.
Supongamos que $\overrightarrow{U}$ y $\overrightarrow{V}$ son ambos observador-vectores. ¿Qué significaría físicamente computar $\overrightarrow{U} + overrightarrow{V}$ ?
Para los vectores como se describe en la parte b, determinar los signos de $(\overrightarrow{U} + \overrightarrow{V}) \cdot (\overrightarrow{U} + \overrightarrow{V})$ y $(\overrightarrow{U} + \overrightarrow{V}) \cdot \overrightarrow{U}$ multiplicándolos. Interpretar el resultado físicamente.

Q16

En la sección 1.5, probamos la desigualdad invertida de Cauchy-Schwarz para dos vectores similares al tiempo, sin ninguna suposición sobre si yacían en el futuro o en el pasado conos de luz. Pero supongamos que solo habíamos establecido este hecho para dos vectores que estaban ambos dirigidos al futuro. Demostrar que la misma desigualdad entonces también tendría que sostenerse independientemente de que uno o ambos vectores fueran dirigidos al pasado.

Q17

En el caso de dos vectores temporales dirigidos al futuro, complete la prueba de la desigualdad del triángulo invertido utilizando el método sugerido en la sección 1.5.

Q18

En la sección 1.5 afirmamos que la desigualdad invertida de Cauchy-Schwarz se mantiene para dos vectores espaciales que abarcan el cono de luz. El propósito de este problema es probar este hecho utilizando el siguiente boceto de un argumento proporcionado por el usuario de PhysicsForums martinbn. Supongamos que los vectores espaciales $\overrightarrow{m}$ y $\overrightarrow{n}$ abarcan el cono de luz, para que podamos encontrar algún número real $\alpha$ tal que $p = \alpha m + n$ sea parecido a la luz. Calcule $p^2$ , y demuestre que ya que $\alpha$ es real, la inequidad invertida de Cauchy- Schwarz sostiene.

Q19

Un objeto de longitud contraída tiene longitud $L = \frac{L_0}{\gamma}$ Joe diferencia esto con respecto al tiempo y encuentra $\frac{dL}{dt} = −L_0v\gamma\frac{dv}{dt}$ . Él razona que no hay límite superior en la magnitud de $\frac{dv}{dt}$ , y por lo tanto si $v \neq 0$ la cantidad $\frac{dL}{dt}$ puede ser arbitrariamente grande. Esto significa que si un objeto acelera alejándose de un observador, su borde de salida puede tener $v > c$ , lo que se supone que está prohibido por la relatividad. ¡OMG! ¿Es correcto el razonamiento de Joe?

Q1

Q2

Q3

Q4

Q5

Q6

Q7

Q8

Q9

Q10

Q11

Q12

Q13

Q14

Q15

Q16

Q17

Q18

Q19

Support Center

How can we help?