1.5: Triángulo y Desigualdades Cauchy-Schwarz

Objetivos de aprendizaje

• Discutir el triángulo y Cauchy-Schwarz

En la geometría euclidiana, tenemos el hecho intuitivamente obvio de que cualquier lado de un triángulo no es mayor que la suma de los otros dos lados. Esto se puede escribir en términos de vectores como\(|m + n| \leq |m| + |n|\). Estrechamente relacionada con ello está la desigualdad\(|m \cdot n| ≤ |m| |n|\), conocida como la desigualdad Cauchy-Schwarz, que se puede ver porque\(m \cdot n = |m| |n| cos\theta\), dónde\(\theta\) está el ángulo entre los dos vectores.

Cualquier prueba de estos hechos depende en última instancia de la suposición de que la métrica tiene la firma euclidiana\(+ + +\) (o de supuestos equivalentes como los axiomas de Euclides). La figura\(\PageIndex{1}\) muestra que por motivos físicos, no esperamos que las desigualdades se mantengan para los vectores Minkowski en sus formas euclidianas no modificadas. La cantidad |m + n| representa el tiempo adecuado de la nave espacial que se movió inercialmente junto con la tierra, mientras que\(|m| + |n|\) es el mayor tiempo adecuado de la nave espacial viajera.

Por otro lado, el espacio Minkowski cuenta con copias del espacio euclidiano incorporadas. Por ejemplo, sabemos que todos los hechos euclidianos familiares deben sostenerse en cualquier plano de simultaneidad definido por un observador particular en un momento dado en el tiempo, ya que la restricción de la métrica a ese plano tiene firma\(---\), y la distinción entre ésta y la\(+ + +\) firma es una arbitraria convención notacional. Resumiendo estas observaciones, esperamos que la versión relativista del triángulo y las desigualdades de Cauchy-Schwarz se dividan en casos, algunos de los cuales son iguales al caso euclidiano y algunos de ellos diferentes.

Algunas cuestiones notacionales pueden resultar confusas en la siguiente discusión. Dejamos\(a^2\) media\(a \cdot a\), que puede no ser positiva, mientras que\(|a|\) indica el número real positivo\(\mid a \cdot a\mid\). Trataré de señalar específicamente cualquier ecuación que sólo sea cierta para la\(+---\) firma y no para\(- + ++\), y expresar resultados finales importantes de una manera que no dependa de esta elección.

Dos vectores similares al tiempo

Figura\(\PageIndex{1}\): La paradoja de los gemelos, interpretada como una desigualdad triangular.

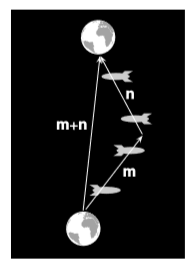
Un caso sencillo e importante es aquel en el que ambos\(m\) y\(n\) trazan posibles líneas mundiales de objetos materiales, como en la figura\(\PageIndex{1}\). Es decir, ambos deben ser vectores parecidos al tiempo. Para ver qué forma de la desigualdad Cauchy-Schwarz debe mantener, dividimos el vector\(n\) en dos partes\(n = n_{\parallel} + n_{\perp}\),, donde\(n_{\parallel}\) es paralela\(m\) y\(n_{\perp}\) perpendicular. Entonces tenemos\(|m · n| = |m · n_{\parallel} | = |m| |n_{\parallel} |\). Pero\(n^2 = (n_{\parallel} + n_{perp} )^2 = n_{\parallel}^2 + 2n_{\parallel} \cdot n_{\perp} + n_{\perp} = n_{\parallel}^2 + n_{\perp}^2\), y como\(n_{\parallel}\) es timelike y\(n_{\perp}\) spacelike, tenemos (en la\(+---\) firma)\(n_{\parallel}^2 > 0\) y\(n_{\perp}^2 < 0\). Por lo tanto, independientemente de la firma\(\lvert n\lvert ≤ \lvert n_{\parallel}\lvert\),, y tenemos la desigualdad de Cauchy-Schwarz invertida

\[|m \cdot n| \geq |m| |n| \quad \text{(valid for either + − −− or − + ++)}\]

Una manera útil de interpretar la inversión en comparación con el caso euclidiano es que si los vectores se normalizan de tal manera que\(|m| = |n| = 1\), entonces\(m \cdot n = \gamma\), ¿dónde\(\gamma\) está el factor Lorentz para un observador cuya línea mundial es paralela\(m\) con respecto a una línea mundial paralela a\(n\) . La diferencia con el comportamiento euclidiano puede entonces entenderse como derivada del hecho de que mientras que\(|cos\theta| ≤ 1\), siempre tenemos\(\gamma \geq 1\).

Dada la motivación física presentada hasta el momento, hubiera sido natural tomar ambas\(m\) y\(n\) mentir en el futuro más que en el cono de luz pasado, pero aún no hemos asumido que ese era el caso, y la inequidad invertida de Cauchy-Schwarz sostiene independientemente de tal suposición. (Ver problema Q16 para una forma alternativa de ver esto.) Sin embargo, para discutir la desigualdad triangular relacionada, tendremos que asumir que ambos vectores están orientados hacia el futuro. Físicamente, esto es necesario para dar la interpretación que se muestra en la figura ai, de la cual ya hemos inferido que se debe revertir la desigualdad triangular. Para verificar esto matemáticamente, podemos calcular la diferencia\((m + n)^2 − (|m| + |n|)^2\) (problema 17).

Dos vectores espaciales que no abarcan el cono de luz

Ahora supongamos que\(m\) y ambos\(n\) son espaciales, y el plano que abarcan no incluye el cono de luz. Operando dentro de este plano, nunca obtenemos vectores similares al tiempo o a la luz, y por lo tanto la naturaleza no euclidiana de la métrica nunca es evidente para nosotros. Por lo tanto, la geometría de este plano es euclidiana, por lo que en este caso deben sostenerse las versiones euclideanas ordinarias del Cauchy-Schwarz y las desigualdades triangulares.

Ejemplo\(\PageIndex{1}\): No relativity required

Supongamos que cierto observador establece coordenadas de Minkowski, y considera los vectores\(\hat{x}\) unitarios y que se\(\hat{y}\) encuentran a lo largo de\(y\) los ejes\(x\) y. El\(x-y\) plano que abarcan no incluye el cono de luz. Al enchufarse a la forma de coordenadas Minkowski de la métrica, encontramos que\(\hat{x} \cdot \hat{y} = 0\), como se esperaba ya que la geometría del\(x-y\) plano es euclidiana. Esto satisface la forma ordinaria de la desigualdad Cauchy-Schwarz.

Dos vectores espaciales que abarcan el cono de luz

Consideremos ahora el caso, en las coordenadas de Minkowski, dónde\(m = (0, 5, 0, 0)\) y\(n = (4, 5, 0, 0)\). Estos vectores abarcan el\(t-x\) plano, cuya geometría no es euclidiana, y no satisfacen la desigualdad euclidiana Cauchy-Schwarz, ya que\(m \cdot n = -25\), mientras que\(|m| |n| = 15\). Dos vectores de este tipo siempre satisfarán la versión invertida de la desigualdad Cauchy-Schwarz (problema Q18). Lo contrario sostiene en el sentido de que si dos vectores espaciales satisfacen la estricta desigualdad\(|m \cdot n| > |m| |n|\), entonces abarcan el cono de luz.