9.1: El Vector Actual

Objetivos de aprendizaje

• Explicar la conservación de la carga

Corriente como flujo de partículas cargadas

Las leyes más fundamentales de la física son las leyes de conservación, que nos dicen que no podemos crear o destruir “cosas”, donde “cosas” podrían significar cantidades como carga eléctrica o energía-impulso. Dado que la carga es una invariante de Lorentz, es un ejemplo fácil para empezar. Debido a que la carga es invariante, también podríamos imaginar que la densidad de carga$ρ$ era invariante. Pero este no es el caso, esencialmente porque el volumen espacial ($3$-dimensional) no es invariante; en$3 + 1$ dimensiones, sólo el volumen cuatridimensional es una invariante. Por ejemplo, supongamos que tenemos un aislante en forma de cubo, con carga distribuida uniformemente a lo largo del mismo según un observador$o_1$ en reposo relativo al cubo. Luego en un marco que$o_2$ se mueve con relación al cubo, paralelo a uno de sus ejes, el cubo se acorta por la contracción de la longitud, y su volumen se reduce por el factor$1/γ$. El resultado es que la densidad de carga en$o_2$ es mayor por un factor de$γ$.

Esto significa que el conocimiento de la densidad de carga$ρ$ en un cuadro es insuficiente para determinar la densidad de carga en otro cuadro. En el ejemplo del cubo, lo que sería suficiente sería el conocimiento del vector$J = ρ_0 v$, dónde$ρ_0$ está la densidad de carga en el cuadro de reposo del cubo, y$v$ es el vector de velocidad del cubo. $J$, denominado vector actual, se transforma como un vector relativista debido a las propiedades de transformación de los dos factores que lo definen. La velocidad$v$ es un vector (sección 3.5). El factor$ρ_0$ es una invariante, ya que a su vez se descompone en carga dividida por resto-volumen. La carga es una invariante, y todos los observadores coinciden en cuál sería el volumen que tendría el cubo en su marco de descanso.

Figura$\PageIndex{1}$: Partículas cargadas con líneas mundiales que contribuyen a$J_x$ y$ρ$. No se muestra la$z$ dimensión, por lo que las 3 superficies cubicas aparecen como cuadrados.

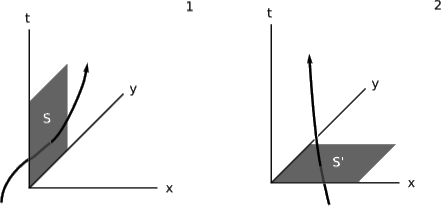
$J$se puede expresar en las coordenadas de Minkowski como$(ρ, J^x, J^y, J^z)$, donde$ρ$ está la densidad de carga y, por ejemplo,$J^x$ es la densidad de la corriente eléctrica en la$x$ dirección. Supongamos que definimos las tres superficies que$S$ se muestran en la figura$\PageIndex{1}$ (1), que consiste en el conjunto de eventos con coordenadas$(t, 0, y, z)$ tales que$0 ≤ t ≤ 1$$0 ≤ y ≤ 1$,, y$0 ≤ z ≤ 1$. Algunas partículas cargadas tienen líneas mundiales que cruzan esta superficie, pasando a través de ella ya sea en la$x$ dirección positiva o en la$x$ dirección negativa (que contamos como transporte de carga negativa). $S$tiene un volumen de tres$V$. Si sumamos el transporte de carga total$∆q$ a través de esta superficie y dividimos por$V$, obtenemos el valor promedio de$J^x$. Si dejamos que se$S$ reduzcan a tres superficies cada vez más pequeñas que rodean el evento$(0, 0, 0, 0)$, entonces obtenemos el valor de$J^x$ en este punto,$lim_{V\to 0} \frac{\Delta q}{V}$. En otras palabras,$J^x$ mide la densidad de flujo de carga que atraviesa$S$. Desde luego esta descripción en términos de un límite implica un gran número de cargos, no sólo uno como en la figura$\PageIndex{1}$.

Puedes escribir la definición análoga para$J^t$, usando una superficie de simultaneidad para like$S'$, figura$\PageIndex{1}$ (2), y verás que expresa la densidad de carga$ρ$. En este caso$S'$ representa un momento en el tiempo, y el flujo a través$S'$ significa que las cargas están cruzando el umbral del pasado al futuro.

Nuestro argumento de que se$J$ transformó como un vector se basó en un caso donde todas las partículas cargadas tenían el mismo vector de velocidad, pero la descripción anterior en términos del flujo de carga eliminó cualquier discusión sobre la velocidad. Es cierto, pero menos obvio, que lo$J$ descrito de esta manera también se transforma como un vector, incluso en los casos en que las partículas cargadas no tienen todas líneas mundiales paralelas. El vector de corriente es la fuente de campos eléctricos y magnéticos. Sorprendentemente, ninguna medición eléctrica macroscópica es capaz de detectar algo más detallado sobre el movimiento de las cargas que la información promedio proporcionada por$J$.

Ejemplo$\PageIndex{1}$: Boosting a solenoid

Figura$\PageIndex{2}$: Solenoide

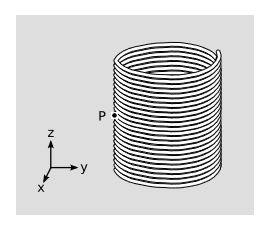
En la figura se$\PageIndex{2}$ muestra un solenoide, en reposo, enrollado a partir de alambre de cobre. En el punto$P$, construimos un bucle ampériano rectangular en el$yz$ plano que tiene su borde derecho dentro del solenoide y su lado izquierdo afuera. Ley de Ampére,

$$\int B\cdot ds = \left ( \frac{4\pi k}{c^2} \right )l$$

entonces nos dice que la densidad de corriente$J_x$ provoca una diferencia entre el campo exterior$B_z = 0$ y el campo interior$B_z = \left ( \frac{4\pi k}{c^2} \right )J_x \Delta y$, donde$∆y$ está el grosor del solenoide. Hay dos cosas que podemos obtener de este resultado, ambas no triviales.

Primero, el campo depende únicamente de la densidad de corriente, no de ninguna información sobre los detalles del movimiento de los electrones en el cobre. El movimiento de los electrones es rápido y altamente aleatorio, pero todo lo que contribuye$J_x$ es la velocidad de deriva lenta, típicamente$∼ 1\: cm/s$, superpuesta a la aleatoriedad. Esto es exacto y nada obvio. Por ejemplo, el impulso total de los electrones sí depende de la parte aleatoria de su movimiento, porque$p_x = mγv_x$ tiene un factor de$γ$ en él.

Segundo, podemos usar las propiedades de transformación del vector de corriente para encontrar el campo de este solenoide en un marco impulsado a lo largo de su eje. Este es el tipo de situación que naturalmente surgiría, por ejemplo, en un motor eléctrico cuyo rotor contiene un electroimán. Una transformación de Lorentz en la$z$ dirección no cambia el$x$ componente de un vector, ni cambia$∆y$, por lo que$B_z$ es lo mismo en ambos fotogramas. Esto no es trivial tanto en el sentido de que hubiera sido difícil de entender por la fuerza bruta como en el sentido de que los campos no tienen que ser los mismos en distintos marcos de referencia —por ejemplo, un impulso en la$x$ o la$y$ dirección habría cambiado el resultado.

Ejemplo$\PageIndex{2}$: A wire

En un conductor sólido como un cable de cobre, tenemos dos tipos de cargas, protones y electrones. Los protones están en reposo en el marco del laboratorio$o$, con densidad de carga$ρ_p$ y densidad de corriente

$$J_p = (ρ_p, 0, 0, 0)$$

en las coordenadas de Minkowski. El movimiento de los electrones es complicado. Algunos electrones están unidos a un átomo en particular, pero aún se mueven a velocidades relativistas dentro de sus átomos. Otros exhiben un movimiento térmico violento que muy cerca, pero no del todo, promedia a cero cuando hay una corriente medible por un amperímetro. Por simplicidad, tratamos a todos los electrones (tanto los ligados como los móviles) como una sola densidad de carga$ρ_e$. Que la velocidad promedio de los electrones, conocida como su velocidad de deriva, esté$v$ en la$x$ dirección. Luego en el marco$o'$ moviéndose junto con la velocidad de deriva tenemos

$$J_{e}^{'} = (\rho _{e}^{'}, 0, 0, 0)$$

que bajo una transformación de Lorentz de nuevo en el marco de laboratorio se convierte

$$J_{e} = (\rho _{e}^{'}\gamma , \rho _{e}^{'}V\gamma , 0, 0)$$

Agregando los dos vectores actuales, tenemos una corriente total en el marco de laboratorio

$$J = (\rho _p + \rho _{e}^{'}\gamma , \rho _{e}^{'}V\gamma , 0, 0)$$

El cable es eléctricamente neutro en este marco, entonces$\rho _p + \rho _{e}^{'}\gamma =0$. Ya que$ρ_p$ es una propiedad fija del alambre, expresamos$\rho _{e}^{'}$ en términos de ello como$ρ_p/γ$. Eliminando$\rho _{e}^{'}$ da

$$J = (0, -ρ_pV, 0, 0)$$

Debido a que los$γ$ factores cancelados, encontramos que la corriente es exactamente proporcional a la velocidad de deriva. Geométricamente, hemos agregado dos vectores similares al tiempo y hemos obtenido uno espacial; esto es posible porque uno de los vectores timelike estaba dirigido hacia el futuro y el otro dirigido al pasado.

Conservación de carga

Figura$\PageIndex{3}$:

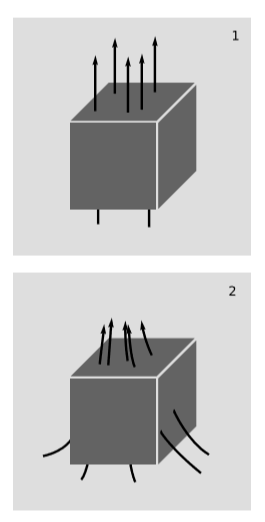
La conservación de la carga se puede expresar elegantemente en términos de$J$. La densidad de carga es el componente similar al tiempo$J^t$. Si esta densidad de carga cercana a cierto punto está, por ejemplo, aumentando, entonces podría deberse a que se ha violado la conservación de carga como en la figura$\PageIndex{3}$ (1). En este ejemplo, más líneas mundiales emergen hacia el futuro en la parte superior del cuatro-cubo de las que habían entrado por la parte inferior en el pasado. Algún proceso dentro del cubo es la creación de carga. En el límite donde el cubo se hace muy pequeño, esto se mediría por un valor de$\frac{\partial J^t}{\partial t}$ que fuera mayor a cero.

Pero los experimentos nunca han detectado ninguna violación de la conservación de carga, por lo que si más carga está emergiendo del lado superior (futuro) del cubo que la que entró desde el fondo (pasado), la explicación más probable es que las cargas no están todas en reposo, como en la figura$\PageIndex{3}$ (1), sino que son móviles, figura$\PageIndex{3}$ (2), y ha habido un flujo neto desde las regiones vecinas del espacio. Debemos encontrar esto reflejado en los componentes espaciales$J^x$,$J^y$ y$J^z$. Además, si todos estos componentes espaciales fueran constantes, entonces cualquier región dada del espacio tendría tanta corriente fluyendo hacia ella desde un lado como fluyendo por el otro. Por lo tanto, necesitamos tener algunas derivadas parciales distintas de cero como$\frac{\partial J^x}{\partial x}$. Por ejemplo, la figura$\PageIndex{3}$ (2) tiene un positivo a$J^x$ la izquierda y un$J^x$ negativo a la derecha, entonces$\frac{\partial J^x}{\partial x} < 0$. La conservación de carga se expresa mediante la ecuación simple$\frac{\partial J^{\lambda }}{\partial x^{\lambda }} = 0$. Escribiendo la suma implícita sobre$λ$, esto dice que

$$\frac{\partial J^t}{\partial t} + \frac{\partial J^x}{\partial x} + \frac{\partial J^y}{\partial y} + \frac{\partial J^z}{\partial z} = 0$$

con una suma implícita sobre el índice$λ$. Si ha tomado cálculo vectorial, reconocerá al operador al que se aplica$J$ como una generalización de cuatro dimensiones de la divergencia. Esta ecuación de conservación de carga es válida independientemente del sistema de coordenadas, por lo que también se puede reescribir en notación de índice abstracto como

$$\frac{\partial J^a}{\partial x^a} = 0$$

Ejemplo$\PageIndex{3}$: Conservation of charge in a solenoid

En un solenoide, tenemos carga circulando a cierta velocidad de deriva$v$. Ignorando los protones, y adaptando la expresión relevante del ejemplo$\PageIndex{2}$ al caso del movimiento circular más que lineal, podríamos tener para la contribución de los electrones al algo actual de la forma

$$J = p(1, -qy, qx, 0),$$

donde$p = γv$ y$q$ depende del$v$ y del radio del solenoide. Se satisface la conservación de la carga, porque cada uno de los cuatro términos de la ecuación

$$\frac{\partial J^t}{\partial t} + \frac{\partial J^x}{\partial x} + \frac{\partial J^y}{\partial y} + \frac{\partial J^z}{\partial z} = 0$$

se desvanece individualmente.