6.5: Agujeros Negros (Parte 2)

Las singularidades también pueden ocurrir sin ninguna explosión en la curvatura. Un ejemplo de ello es una singularidad cónica, Figura 6.3.2. (Cf. Figura 5.9.2) En la relatividad 2+1-dimensional, la curvatura desaparece de manera idéntica en el caso de un vacío, y el único tipo de singularidad de curvatura que podemos tener es una singularidad de no curvatura. Otro ejemplo de una singularidad de no curvatura lo proporciona la familia de espacio-tiempos Taub-nut, en la que algunas geodésicas parecidas a la luz se enrollan hacia un horizonte, pero las fuerzas mareales no explotan en el horizonte. No hay razón clara para esperar que las singularidades de no curvatura puedan existir realmente en nuestro universo, pero tampoco hay ninguna prueba de que no puedan formarse por procesos naturales.

Figura\(\PageIndex{2}\): Una singularidad cónica. El cono tiene curvatura intrínseca cero en todas partes excepto en su punta. El geodésico 1 puede extenderse infinitamente lejos, pero el geodésico 2 no puede; dado que la métrica no está definida en la punta, no hay una manera sensata de definir cómo se debe extender el geodésico 2.

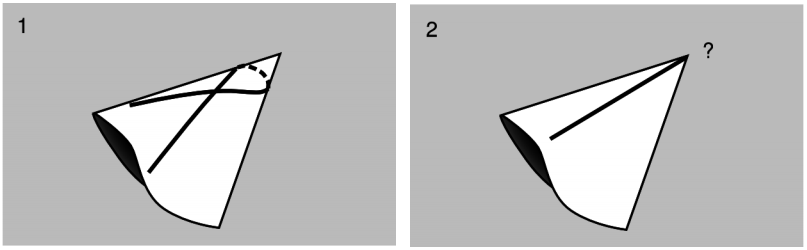
Ejemplo 4: Una singularidad sin curvatura

Considere la métrica

\[ds^{2} = \frac{1}{t} dt^{2} - t \,d \theta^{2}\]

en 1+1 dimensiones, donde\(\theta\) hay un ángulo que discurre alrededor del círculo. Esta es una versión simplificada de un espacio-tiempo de tuerca Taub. Las geodésicas similares a la luz tienen ds\(\frac{dt}{t}\) = 0, así = ± d\(\theta\), y\(\theta\) = (const) ± ln (±t), donde los dos signos se pueden elegir de forma independiente. Destaca el geodésico\(\theta\) = ln t, que se define sólo para t > 0. Envuelve el círculo infinitamente muchas veces a medida que t va a cero, y nos gustaría saber si ahí está incompleto. Si el parámetro afín va al infinito a medida que t se acerca a cero, entonces el geodésico no está incompleto.

Los símbolos de Christoffel que no se desvanecen son\(\Gamma^{t}_{tt} = − \frac{1}{2t}, \Gamma^{\theta}_{\theta t} = \Gamma^{\theta}_{t \theta} = \frac{1}{2t}\), y\(\Gamma^{t}_{\theta \theta} = \frac{t}{2}\) (Problema 3). Las ecuaciones geodésicas resultantes son

\[\begin{split} \ddot{t} &= \frac{\dot{t}^{2}}{2t} - \frac{t}{2} \dot{\theta}^{2} \\ \ddot{\theta} &= - \frac{\dot{t}}{\dot{\theta}} t, \end{split}\]

donde los puntos representan la diferenciación con respecto al parámetro afín\(\lambda\). Diferenciación implícita de la ecuación\(\theta\) = ln t da\(\dot{\theta} = \frac{\dot{t}}{t}\), y conectarlo a la primera ecuación geodésica da como resultado\(\ddot{t}\) = 0. Por lo tanto, podemos tomar t =\(\lambda\). (También podríamos tomar t = a\(\lambda\) + b, lo que resultaría en un parámetro afín diferente e igualmente válido). Si λ hubiera ido a\(− \infty\) como t fue a cero, entonces habríamos demostrado que la geodésica estaba completa. En cambio, se acerca a un límite finito, lo que sugiere, pero no prueba, que está incompleto.

El cambio de coordenadas\(\theta \rightarrow \theta\) − ln t permite que las geodésicas similares a la luz en sentido antihorario continúen a través de t = 0. (Debido a que esta transformación no es un diffeomorfismo, no es solo un cambio de nombre de puntos sino un cambio físico real en la estructura del espacio-tiempo; equivale a cortar las mitades con t < 0 and t > 0 y volver a unirlas de una manera diferente). Sin embargo, las geodésicas correspondientes en el sentido de las agujas del reloj permanecen incompletas. Un cambio diferente de coordenadas se extiende hacia las agujas del reloj pero no las antihorario. En todos los casos hay geodésicas incompletas, por lo que aún parece que sí tenemos una singularidad. Dado que las singularidades de curvatura no existen en menos de 3+1 dimensiones, esta es una singularidad de no curvatura. (Un cálculo también muestra que este espacio-tiempo en particular es plano).

Una singularidad no se considera un punto o conjunto de puntos en un espacio-tiempo; es más como un agujero en la topología del colector. Por ejemplo, el Big Bang no ocurrió en un punto o conjunto de puntos. Una singularidad representa un desglose en la métrica, y sin una métrica tal vez ni siquiera podamos distinguir la diferencia entre un punto y muchos. Para más información sobre estos temas, consulte las discusiones sobre construcciones de límites en la sección 7.3. Hay un sentido en el que una singularidad de agujero negro no es una cosa en absoluto, y no tiene características definibles; sección 7.4.

Ejemplo 5: ¿Un punto, o muchos?

Supongamos que tengo un espacio bidimensional con coordenadas (u, v), y te pregunto si S = {(u, v) |v = 0} es un punto o una curva, mientras me niego a divulgar qué métrica tengo en mente. Probablemente dirías que S era una curva, y si la métrica fuera ds ² = du ² +dv ², tendrías razón. Por otro lado, si la métrica fuera ds ² = v ² du ² + dv ², S sería un punto.

Este fue un ejemplo donde había dos posibles métricas que podíamos imaginar. A una singularidad, es aún peor. No hay métrica posible que podamos extender a la singularidad.

Debido a que una singularidad no es un punto o un conjunto de puntos, no podemos definir su carácter temporal o espacial de la manera que lo haríamos con, digamos, una curva. Una singularidad similar al tiempo, también conocida como una singularidad localmente desnuda, es tal que un observador con una línea mundial similar al tiempo puede tener la singularidad a veces en su futuro cono de luz y a veces en su cono de luz pasado. ¹⁸

Las singularidades de Schwarzschild y Big Bang son espaciosas. (Tenga en cuenta que en la métrica Schwarzschild, las coordenadas r y t de Schwarzschild intercambian sus caracteres similares al tiempo y al espacio dentro del horizonte de eventos). La definición de una singularidad temporal es local. Una singularidad tipo tiempo sería aquella que podrías tener sentada en tu escritorio, donde podrías mirarla y meterla con un palo.

Una singularidad desnuda es aquella a partir de la cual pueden originarse las líneas mundiales parecidas al tiempo o a la luz y luego escapar al infinito. La singularidad de la métrica Schwarzschild no está desnuda. Esta noción es global.

Acumulan evidencias contra la censura cósmica

A partir de 2017, se están acumulando pruebas de que la censura cósmica es falsa. Ya en 1969, cuando Roger Penrose formuló por primera vez la hipótesis, los relativistas habían sido fuertemente influenciados por un cálculo de 1939 de Oppenheimer y Snyder para el colapso gravitacional de una nube uniforme y esférica de “polvo”, que significa partículas materiales que actúan como un fluido ideal sin presión (ver ejemplo 1). (Cf. Sección 4.4 sobre el límite Tolman-Oppenheimer-Volkoff, derivado antes del mismo año.) A pesar de que Oppenheimer y Snyder fueron demasiado tímidos para continuar el cálculo más allá de la formación de un horizonte de eventos, su resultado no fue tomado en serio durante años, siendo la noción de un colapso gravitacional desbocado demasiado distante del estado de la técnica en términos de observación. Pero después los trabajadores sí completaron el cálculo. Encontraron que se desarrolló una singularidad, pero que el horizonte se formó lo suficientemente temprano como para ocultarlo, de manera que ningún geodésico parecido al tiempo o a la luz de la singularidad pudiera escapar a un observador distante. Esto fue consistente con una versión débil de la hipótesis de la censura cósmica, que una singularidad (globalmente) desnuda no puede formarse a partir del colapso gravitacional.

Pero interpretar el resultado como evidencia de censura cósmica era engañoso. En retrospectiva, hay claras razones newtonianas para sospechar que una nube perfectamente homogénea tiene propiedades que son un poco demasiado especiales. En la versión newtoniana el campo gravitacional interno es proporcional a r. Partiendo del reposo en r, una partícula tiene que recorrer una distancia r para llegar al centro, pero como la aceleración es proporcional a r, el tiempo necesario para llegar al centro es el mismo para todas las partículas. Hay una singularidad newtoniana de densidad infinita, y esto ocurre al mismo tiempo para todas las partículas, que es después de la formación de una superficie a partir de la cual la velocidad de escape tiene algún valor fijo, como c. Por lo tanto, en términos newtonianos, la censura cósmica se mantiene, pero solo sostiene por la perfecta homogeneidad de la nube.

De hecho, la versión general-relativista del colapso gravitacional no homogéneo ya había sido elaborada hacia 1933 por Lemaître, Tolman y Bondi, nuevamente para el caso de una nube esférica, pero ahora con un perfil de densidad\(\rho\) (r). Esta familia de métricas, llamada las métricas Lemaître-Tolman-Bondi, es lo suficientemente general como para incluir modelos de expansión cosmológica así como modelos de colapso gravitacional local. Tolman aplicó el modelo de colapso a la formación de “nebulosas”, es decir, galaxias, en el universo temprano, pero no siguió la evolución del colapso hasta su dénouement ultrarelativista, como lo habían hecho Oppenheimer y Snyder. Cuando uno lo hace, lidiando con algunos obstáculos técnicos e imponiendo algunas limitaciones para la razonabilidad física, resulta que en la mayoría de los casos, el resultado es una singularidad localmente desnuda. ¹⁹ Es decir, se requiere un ajuste fino para producir algo más parecido a un agujero negro estándar. Queda por ver si esto es cierto cuando se relaja la restricción de la perfecta simetría esférica.

Esto no significa necesariamente de cara que la censura cósmica esté muerta, ya que los espacio-tiempos con simetría esférica están ellos mismos finamente afinados en algún sentido, sino que es más bien un desarrollo dramático, ya que la gente había imaginado desde hace 75 años, basado en los cálculos de Oppenheimer-Snyder para polvo homogéneo, que un agujero negro era el resultado genérico del desbocado colapso gravitacional. La censura cósmica es en cierto sentido imposible de desmentir, ya que parte del programa de investigación es encontrar la definición más adecuada de la conjetura, pero estos resultados sugieren que para que sea verdad, entonces hay que debilitarla tanto como para ser de poco interés. En general, una definición significativa de lo que significa violar la débil censura cósmica probablemente debería incluir algo así como los siguientes ingredientes.

1. Las condiciones iniciales no hacen disponible una cantidad infinita de energía dentro de una región finita.
2. Las condiciones iniciales no contienen singularidades.
3. Las geodésicas incompletas parecidas a la luz pueden llegar a un observador distante.
4. Tal violación aún ocurre si imponemos pequeñas perturbaciones en los datos iniciales.
5. Las formas de la materia son físicamente realistas.

Si no imponemos algo así como la condición 1, entonces podemos establecer condiciones iniciales que no son de interés porque no son realistas. Por esta razón, se suele estudiar espacio-tiempos que son asintóticamente planos. ²⁰ La condición 2 expresa la idea de que las singularidades que se produzcan deben ser nuevas formadas por el colapso gravitacional. La violación a la censura se expresa mediante la condición 3. La noción de observador distante se puede formalizar aún más al exigir que tal geodésico llegue al infinito nulo, I +; ver p. 265. Si se omite 4, entonces se conocen claros contraejemplos a la censura. Sin embargo, no se sabe si aquí existe una manera adecuadamente rigurosa de definir “pequeñas perturbaciones”. ²¹ Se espera que los campos de materia realistas, 5, por ejemplo, no tengan masa negativa. ²²

Debido a que la débil censura cósmica parece ser violada si se describe por estas cinco condiciones, la gente ha comenzado a buscar condiciones adicionales que pudieran salvar la conjetura.

Wald ²³ sugiere agregar un sexto requisito. Propone que los tipos de materia se restrinjan aún más a aquellos que tengan la propiedad de que si la métrica es fija, más que dinámica como en la relatividad general, entonces no ocurren singularidades. Esto me parece una condición demasiado fuerte, y hay indicios de que no es suficiente.

Nota

²⁰ La planitud asintótica se introdujo de manera informal en la sección 4.5 y se define en detalle en la sección 7.4. También puede ser necesario imponer un requisito de que los campos de materia se caigan a algún ritmo a medida que vamos al infinito.

²¹ En términos técnicos, no tenemos ninguna topología o medida definida en el conjunto de todas las condiciones iniciales posibles. En el trabajo real hasta la fecha, las personas han seleccionado algún conjunto de posibles condiciones iniciales, descritas por un pequeño número de parámetros ajustables, y luego han intentado probar la condición 4 usando una topología y medida aparentemente natural definida en el espacio de esos parámetros.

²² De manera más rigurosa, esperamos que satisfagan las condiciones energéticas adecuadas, sección 8.1.

Otra propuesta está en la siguiente línea. Cuando se produce una singularidad desnuda, entonces tenemos una región de espacio-tiempo para la cual la singularidad se encuentra dentro del cono de luz pasado. La superficie parecida a la luz que constituye el límite de esta región se llama horizonte Cauchy. Un observador que pasa más allá del horizonte de Cauchy puede observar información arbitraria, es decir, fenómenos no predichos por ninguna ley de la física, y flujos infinitos de energía. Roger Penrose ha señalado, sin embargo, que en ciertos casos ilustrativos, existe una tendencia a que la energía de todo el espacio-tiempo previo a la singularidad se centre en el horizonte de Cauchy. El resultado podría entonces ser que tal observador sea destruido al pasar por el horizonte de Cauchy. En otras palabras, el horizonte de Cauchy en realidad se convierte en una singularidad. El mecanismo de Penrose parece fallar, sin embargo, para un espacio-tiempo con una constante cosmológica positiva, que es lo que realmente tenemos en nuestro universo.

Radiación Hawking

Radiación de agujeros negros

Dado que se espera que los horizontes de eventos emitan radiación de cuerpo negro, un agujero negro no debe ser completamente negro; debe irradiar. Esto se llama radiación Hawking. Supongamos que la observadora B justo afuera del horizonte de eventos explota los motores de su cohete, produciendo suficiente aceleración para evitar ser absorbida. Por el principio de equivalencia, lo que observa no puede depender de si la aceleración que experimenta se debe en realidad a un campo gravitacional. Por lo tanto, detecta radiación, que interpreta como proveniente del horizonte de eventos debajo de ella. A medida que se acerca cada vez más al horizonte, la aceleración se acerca al infinito, por lo que la intensidad y frecuencia de la radiación crece sin límite.

Un observador distante A, sin embargo, ve una imagen diferente. Según A, el tiempo de B está extremadamente dilatado. A ve la aceleración de B como siendo solo ∼ 1/m, donde m es la masa del agujero negro; A no percibe esta aceleración como soplando hasta el infinito cuando B se acerca al horizonte. Cuando A detecta la radiación, está extremadamente desplazada al rojo, y tiene el espectro que uno esperaría para un horizonte caracterizado por una aceleración a ∼ 1/m. El resultado para un agujero negro de 10 masas solar es T ∼ 10 ⁻⁸ K, que es tan bajo que el agujero negro en realidad está absorbiendo más energía del radiación cósmica de fondo de microondas que emite.

Por lo tanto, la observación directa de la radiación de agujeros negros probablemente solo sea posible para agujeros negros de masas muy pequeñas. Estos pueden haber sido producidos poco después del big bang, o es concebible que puedan ser creados artificialmente, por tecnología avanzada. Si existe radiación de agujero negro, puede ayudar a resolver la paradoja de la información, ya que es posible que la información que entra en un agujero negro se libere eventualmente a través de correlaciones sutiles en la radiación de cuerpo negro que emite.

Física de partículas

La radiación Hawking tiene algunas propiedades intrigantes desde el punto de vista de la física de partículas. En un acelerador de partículas, la lista de partículas que se pueden crear en cantidades apreciables está determinada por constantes de acoplamiento. En la radiación Hawking, sin embargo, esperamos ver un muestreo representativo de todo tipo de partículas, sesgado solo por el hecho de que las partículas sin masa o de baja masa tienen más probabilidades de producirse que las masivas. Por ejemplo, se ha especulado que parte de la materia oscura del universo existe en forma de partículas “estériles” que no se acoplan a ninguna fuerza salvo la gravedad. Tales partículas nunca se producirían en aceleradores de partículas, sino que se verían en la radiación Hawking. Con base en el conocimiento actual de la física de partículas, se espera que los principales componentes de la radiación Hawking, para todos menos los agujeros negros más microscópicos, sean fotones y gravitones, que competirían en términos aproximadamente iguales, dependiendo del momento angular del agujero negro. ²⁴

La radiación Hawking violaría muchas leyes de conservación preciadas de la física de partículas. Deja que un átomo de hidrógeno caiga en un agujero negro. Hemos perdido un leptón y un barión, pero si queremos preservar la conservación del número de leptón y el número de bariones, cubrimos esto con una hoja de higuera diciendo que el agujero negro simplemente ha aumentado su número de leptones y número de bariones en +1 cada uno. Pero eventualmente el agujero negro se evapora, y la evaporación es probablemente principalmente en partículas de masa cero como los fotones. Una vez que el agujero se ha evaporado completamente, nuestra hoja de higuera también se ha evaporado. Ahora no hay ningún objeto físico al que podamos atribuir las +1 unidades del número de leptón y barión.

Complementariedad de agujeros negros

Una pregunta muy difícil sobre la relación entre la mecánica cuántica y la relatividad general ocurre de la siguiente manera. En nuestro ejemplo anterior, el observador A detecta un espectro de luz extremadamente desplazado al rojo procedente del agujero negro. A interpreta esto como evidencia de que el espacio cercano al horizonte de eventos es en realidad una intensa vorágine de radiación, con la temperatura acercándose al infinito a medida que uno se acerca cada vez más al horizonte. Si B regresa de la región cercana al horizonte, B estará de acuerdo con esta descripción. Pero supongamos que el observador C simplemente cae recto por el horizonte. C no siente ninguna aceleración, por lo que por el principio de equivalencia C no detecta ninguna radiación en absoluto. Al pasar por el horizonte de eventos, C dice: “¡A y B son mentirosos! No hay radiación en absoluto”. A y B, sin embargo, C ven como haber entrado en una región de radiación infinitamente intensa. “Ah”, dice A, “lástima. C debería haber dado la vuelta antes de que se pusiera demasiado caliente, tal como lo hice yo”. Este es un ejemplo de un principio que hemos encontrado antes, que cuando se combinan la gravedad y la mecánica cuántica, diferentes observadores no están de acuerdo sobre el número de cuantos presentes en el vacío. Se nos presenta una paradoja, porque A y B creen en una versión completamente diferente de la realidad que C. A y B dicen que C era fricasí, pero C sabe que eso no sucedió. Una sugerencia es que esta contradicción muestra que la lógica apropiada para describir la gravedad cuántica es nonaristotélica, como se describe en la sección 2.3. Esta idea, sugerida por Susskind et al., lleva el nombre de complementariedad de agujero negro, por analogía con la descripción filosófica de Niels Bohr de la dualidad onda-partícula como “complementaria” más que contradictoria. En esta interpretación, tenemos que aceptar el hecho de que C experimenta una realidad cualitativamente diferente a A y B, y nos consolamos al reconocer que la contradicción nunca puede llegar a ser demasiado aguda, ya que C se pierde detrás del horizonte de eventos y nunca puede volver a enviar información.

Agujeros Negros en Dimensiones d

Se ha propuesto que nuestro universo podría tener en realidad no d = 4 dimensiones sino algún número mayor, siendo las d − 4 “extra” parecidas al espacio, y acurrucadas en alguna pequeña escala\(\rho\) para que no las veamos en la vida ordinaria. Un candidato para tal escala\(\rho\) es la longitud de Planck, y luego tenemos que hablar de teorías de la gravedad cuántica como la teoría de cuerdas. Por otro lado, podría ser la escala electrodébil de 1 TeV; la motivación para tal idea es que permitiría la unificación de las interacciones electrodébiles con la gravedad. Esta idea se conoce con el nombre de “grandes dimensiones extra” — “grandes” porque\(\rho\) es más grande que la longitud de Planck. De hecho, en tales teorías la longitud de Planck es la escala de unificación electrodébil, y el número normalmente denominado longitud de Planck no es realmente la longitud de Planck. ²⁵

En las dimensiones d, hay dimensiones espaciales d−1, y una superficie de simetría esférica tiene d − 2. En el límite newtoniano de campo débil, la densidad de las líneas de campo gravitacional cae como\(\frac{m}{r^{d−2}}\) con la distancia de una fuente m, y por lo tanto encontramos que la ley de gravedad de Newton tiene un exponente de − (d − 2). Si d ≠ 3, podemos integrarnos para encontrar que el potencial gravitacional varía como\(\Phi\) ∼ −mr ^{− (d−3)}. Pasando de nuevo al límite de campo débil de la relatividad general, el principio de equivalencia dicta que el término g _tt de la métrica sea aproximadamente 1 + 2\(\Phi\), por lo que encontramos que la métrica tiene la forma

\[ds^{2} \approx (1 − 2mr^{−(d−3)}) dt^{2} − (\ldots) dr^{2} − r^{2} d \theta^{2} − r^{2} \sin^{2} \theta \,d \phi^{2} \ldotp\]

Esto se parece a la forma Schwarzschild sin otro cambio que una generalización del exponente, y de hecho Tangherlini demostró en 1963 que para d > 4, se obtiene la solución exacta simplemente aplicando el mismo cambio de exponente a g _rr también. ²⁶

Si existen grandes dimensiones adicionales, entonces esta es la forma real de cualquier espacio-tiempo de agujero negro para r <<\(\rho\), donde la curvatura de fondo de las dimensiones adicionales es insignificante. Dado que todos los exponentes cambian, las fuerzas gravitacionales se vuelven más fuertes de lo que se esperaba de otra manera a pequeñas distancias, y se vuelve más fácil hacer agujeros negros. Se ha propuesto que si existen grandes dimensiones adicionales, se observarían agujeros negros microscópicos en el Gran Colisionador de Hadrones. Inmediatamente se evaporarían en radiación Hawking, con una firma experimental de violar las leyes de conservación estándar de la física de partículas. A partir de 2010, los resultados empíricos parecen ser negativos. ²⁷

El razonamiento dado anteriormente falla en el caso de d = 3, es decir, 2+1- espacio-tiempo dimensional, tanto porque la integral de r ⁻¹ no es r ⁰ como porque la métrica Tangherlini-Schwarzschild no es una solución de vacío. Como se muestra en el problema 12, no hay contraparte de la métrica Schwarzschild en 2+1 dimensiones. Esto se debe esencialmente a que para d = 3 la masa es sin unidades, por lo que dada una fuente que tiene una cierta masa, no hay forma de establecer la escala de distancia a la que el comportamiento newtoniano de campo débil da paso al campo fuerte relativista. Mientras que para d ≥ 4, la gravedad newtoniana es el caso limitante de la relatividad, para d = 3 son teorías no relacionadas. De hecho, la teoría relativista de la gravedad para d = 3 es algo trivial. El espacio-tiempo no admite curvatura en soluciones de vacío, ²⁸ por lo que la única forma no trivial de hacer espaciotiempos no Minkowski 2+1-dimensionales es pegando piezas de Minkowski en diversas topologías, como pegar trozos de papel para hacer cosas como conos y tiras de M¨obius. gravedad 2+1-dimensional tiene singularidades cónicas, pero no las de estilo Schwarzschild que están rodeadas de espacio-tiempo curvo.

Si existen soluciones de agujeros negros en dimensiones d, entonces se puede extender dicha solución a dimensiones d+1 con simetría cilíndrica, formando una “cuerda negra”. La inexistencia de d = 3 agujeros negros implica que las soluciones de cuerdas negras no existen en nuestro propio universo d = 4. Sin embargo, diferentes consideraciones surgen en un universo con una constante cosmológica negativa. Luego hay soluciones 2+1-dimensionales conocidas como agujeros negros BTZ. ²⁹ Como nuestro propio universo tiene una constante cosmológica positiva, no negativa, todavía encontramos que las cuerdas negras no pueden existir.

Referencias

¹⁸ Penrose, Radiación gravitacional y colapso gravitacional; Actas del Simposio, Varsovia, 1973. Dordrecht, D. Reidel Publishing Co. pp. 82-91, gratis en línea en Adsabs.Harvard.edu/Full/1974iaus... 64... 82P

¹⁹ Joshi y Malafarina, arxiv.org/abs/1405.1146

²³ “Colapso gravitacional y censura cósmica”, arxiv.org/abs/gr-qc/ 9710068

²⁴ Dong, arxiv.org/abs/1511.05642

²⁵ Kanti, arxiv.org/abs/hep-ph/0402168

²⁶ Emparan y Reall, “Agujeros Negros en Dimensiones Superiores”, relatividad. livingreviews.org/articles/LRR-2008-6/

²⁷ http://arxiv.org/abs/1012.3375

²⁸ arxiv.org/abs/gr-qc/0503022v4

²⁹ arxiv.org/abs/gr-qc/9506079v1