6.6: Soluciones degeneradas

Esta sección se puede omitir en una primera lectura.

En el horizonte de eventos del espacio-tiempo Schwarzschild, los roles temporales y espaciales del Schwarzschild\(r\) y las\(t\) coordenadas se intercambian alrededor, de modo que los signos en la métrica cambian de +−−− a − + −−. Al discutir casos como este, resulta conveniente definir un nuevo uso del término “firma”, como s = p − q, donde p es el número de signos positivos y q el número de negativos. Esto también puede ser representado por el par de números (p, q). El ejemplo del horizonte Schwarzschild no es demasiado perturbador, tanto porque el comportamiento gracioso surge ante una singularidad que puede ser eliminada por un cambio de coordenadas como porque la firma permanece igual. Un observador que cae libre por el horizonte observa que las propiedades locales del espacio-tiempo permanecen iguales, con |s| = 2, como lo exige el principio de equivalencia.

Pero esto sólo nos hace preguntarnos si hay otros ejemplos en los que un observador realmente detectaría un cambio en la firma de la métrica. Se nos anima a pensar en la firma como algo empíricamente observable porque, por ejemplo, se ha propuesto que nuestro universo puede tener dimensiones espaciales adicionales antes insospechadas, y estas teorías hacen predicciones comprobables. Como no notamos las dimensiones adicionales en la vida ordinaria, tendrían que envolverse en una topología cilíndrica. Algunas de esas teorías, como la teoría de cuerdas, son intentos de crear una teoría de la gravedad cuántica, por lo que se supone que el radio cilíndrico está en el orden de la longitud de Planck, que corresponde cuánto-mecánicamente a una escala de energía que no podremos sondear utilizando ninguna tecnología previsible. Pero también es posible que el radio sea grande —posibilidad que se conoce con el nombre de “grandes dimensiones extra ”— para que pudiéramos ver un efecto en el Gran Colisionador de Hadrones. Nada en la formulación de las ecuaciones de campo de Einstein requiere una firma 3+1 (i.e., (1, 3)), y funcionan igualmente bien si la firma es en cambio 4+1, 5+1,. La ley de gravedad del cuadrado inverso de Newton se describe por la relatividad general como derivada de la naturaleza tridimensional del espacio, por lo que en pequeñas escalas en una teoría con n grandes dimensiones adicionales, el comportamiento de 1/r ² cambia a 1/r ²⁺ⁿ, y es posible que el LHC pudiera producir agujeros negros microscópicos, que inmediatamente se evaporarían en radiación Hawking de una manera característica.

Entonces parece que la firma del espacio-tiempo es algo que no es cognoscible a priori, y debe determinarse por experimento. Cuando se supone que una cosa es experimentalmente observable, la relatividad general nos dice que es mejor que sea independiente de la coordinación. ¿Esto es así? Una proposición del álgebra lineal llamada ley de inercia de Sylvester nos anima a creer que es. El teorema establece que cuando una matriz real\(A\) es diagonalizada por un cambio de base real, no singular (una transformación de similitud S ⁻¹ AS), el número de elementos diagonales positivos, negativos y cero se determina de manera única. Dado que un cambio de coordenadas tiene el efecto de aplicar una transformación de similitud en la métrica, parece que la firma es independiente de coordenadas.

Esto no es del todo correcto, sin embargo, como lo demuestra la siguiente paradoja. La invarianza coordinada de la relatividad general nos dice que si todos los relojes, en todas partes del universo, se ralentizaran simultáneamente (con simultaneidad definida de la manera que nos guste), no habría consecuencias observables. Esto implica que el espacio-tiempo

\[ds^2 = −t \,dt^2 − d \ell^{2},\]

donde

\[d \ell^{2} = dx^2 + dy^2 + dz^2,\]

es empíricamente indistinguible de un espacio-tiempo plano. Partiendo de t =\(− \infty\), el componente positivo g _tt de la métrica se contrae uniformemente, lo que debería ser inofensivo. De hecho podemos verificar por evaluación directa del tensor Riemann que se trata de un espacio-tiempo plano (problema 10). Pero para t > 0 la firma de la métrica cambia de + − −− a − − − −, es decir, de Lorentzian (|s| = 2) a Euclidean (|s| = 4). Esto es preocupante. Para t < 0, la métrica es una descripción perfectamente válida de nuestro propio universo (que es aproximadamente plano). El tiempo pasa, y no hay señales de ningún desastre inminente. Entonces, de repente, en algún momento, toda la estructura del espacio-tiempo sufre un horrible espasmo. Esto es una paradoja, porque bien podríamos haber planteado nuestras condiciones iniciales usando algún otro sistema de coordenadas, en el que la métrica tenía la forma familiar ds ² = dt ² −d\(\ell^{2}\). Se supone que la relatividad general es agnóstica sobre las coordenadas, pero una elección de coordenadas conduce a una predicción diferente sobre la firma, que es una cantidad independiente de coordenadas.

Nos llevan a la resolución de la paradoja si construimos explícitamente la transformación coordinada involucrada. En las coordenadas (t, x, y, z), tenemos ds ² = −t dt ² − d\(\ell^{2}\). Nos gustaría encontrar la relación entre t y alguna otra coordenada u tal que recuperemos la forma familiar ds ² = du ² −d\(\ell^{2}\) para la métrica. La ley de transformación del tensor da

\[\begin{split} g_{tt} &= \left(\dfrac{\partial u}{\partial t}\right)^{2} g_{uu} \\ -t &= \left(\dfrac{\partial u}{\partial t}\right)^{2} \end{split}\]

con solución

\[u = \pm \frac{2}{3} t^{\frac{3}{2}}, \quad t < 0 \ldotp\]

No hay solución para t > 0.

Figura\(\PageIndex{1}\) - El cambio de coordenadas es degenerado a t = 0.

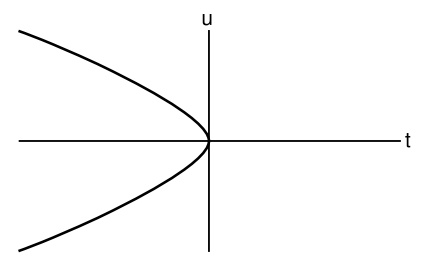
Si los físicos que viven en este universo, a t < 0, por alguna razón eligen t como su coordenada de tiempo, de hecho hay una manera de decir que el evento cataclísmico a t = 0 no es una predicción confiable. En t = 0, el componente de tiempo de su métrica desaparece, por lo que su firma cambia de + − −− a 0 − −−. En ese momento, la maquinaria de la formulación tensora estándar de relatividad general se descompone. Por ejemplo, ya no se pueden subir índices, porque g ^ab es la matriz inversa de g _ab, pero g _ab no es invertible. Dado que las ecuaciones de campo se expresan en última instancia en términos de la métrica utilizando maquinaria que incluye subir y bajar índices, no hay forma de aplicarlas a t = 0. No hacen una falsa predicción del fin del mundo; no logran hacer ninguna predicción en absoluto. Los físicos acostumbrados a trabajar en términos de la coordenada t pueden simplemente levantar las manos y decir que no tienen forma de predecir nada a t > 0. Pero ya saben que su espacio-tiempo es aquel cuyos observables, como la curvatura, son todos constantes con respecto al tiempo, por lo que deberían preguntarse por qué se rompe esta simetría perfecta al señalar t = 0. No hay físicamente nada que deba hacer que un momento en el tiempo sea diferente a cualquier otro, por lo que elegir un tiempo particular para llamar a t = 0 debe interpretarse meramente como una elección arbitraria de la ubicación del origen del sistema de coordenadas. Esto sugiere a los físicos que todos los problemas que han estado teniendo no son problemas con ningún significado físico, sino meramente problemas derivados de una mala elección de coordenadas. Realizan el cálculo anterior, y descubren la coordenada de tiempo u. Expresado en términos de u, la métrica se comporta bien y la maquinaria de predicción nunca se descompone.

La paradoja planteada anteriormente se resuelve porque la ley de inercia de Sylvester solo se aplica a una transformación no singular S. Si S hubiera sido singular, entonces la S ⁻¹ mencionada en el teorema no habría existido ni siquiera. Pero la transformación de u a t tiene\(\frac{\partial t}{\partial u}\) = 0 a u = t = 0, por lo que es singular. Todo ello de acuerdo con la filosofía general de la invarianza coordinada en la relatividad, que es que sólo se permiten transformaciones de coordenadas suaves, uno a uno. Alguien que haya encontrado una coordenada afortunada como u, y que luego contemple transformarse a t, debería darse cuenta de que no es una buena idea, porque la transformación no es suave y uno-a-uno. Alguien que ha comenzado por trabajar con una coordenada desafortunada como t encuentra que la maquinaria se descompone a t = 0, y concluye que sería una buena idea buscar un conjunto de coordenadas más útil. Esta situación en realidad puede surgir en cálculos prácticos.

¿Qué pasa con nuestra pregunta original: ¿podría cambiar realmente la firma del espacio-tiempo en algún límite? Ahora la respuesta es clara. Tal cambio de firma es algo que posiblemente podría tener un significado físico intrínseco, pero si es así, entonces la formulación estándar de la relatividad general no es capaz de hacer predicciones al respecto. Existen otras formulaciones de relatividad general, como la de Ashtekar, que ordinariamente son equivalentes a las de Einstein, pero que son capaces de hacer predicciones sobre cambios de firma. Sin embargo, hay más de una formulación de este tipo, y no están de acuerdo en sus predicciones sobre los cambios de firma.